AI学习时间 06 - Transformer 与自注意力机制 1
#大语言模型 #时序数据
#Transformer #自注意力机制
书籍推荐
- 《Grokking Deep Learning》 - Andrew W. Trask
⭐⭐⭐⭐⭐
- Grokking 系列的书都非常易懂
- 例子,图解,严格定义表述,代码实现四合一
- 《大语言模型》 - 赵鑫等 ⭐⭐⭐⭐
- 非常详尽的大语言模型介绍
- 内容非常精炼,信息量巨大,不过比较严肃严谨,公式原理较多
- 《Build a Large Language Model》 - Sebastian
Raschka ⭐⭐⭐⭐⭐
- 从零开始实现一个 LLM
- 原理讲述非常清晰,由浅入深
Transformer 架构
之前提到大语言模型本质是一个函数,输入一个文本,输出一个文本,而文本本身是序列信息,输出的时候是一个个字输出的,所以这个函数的本质是输入一个序列,输出一个字。大语言模型在预训练的时候已经学习了语言模型,也就是给定上文,预测下文的概率,再根据一定的解码策略生成这个具体的下文。
那这个函数的结构是怎样的呢?如何对这个根据序列生成下文概率分布的问题建模?
时序数据
之前提到的例子里,基本上都不是时序数据。比如根据当前棋局生成下一步棋,或者根据图片分析类别,对于“当前棋局”,或者“图片”来说,都是一个静态的输入,和时序没有关系。
// 选择下一步棋 |
但是考虑大语言模型的基本问题,输入上文,生成下文,下文是一个句子,但是大模型一次只能生成一个字,所以内部必然存在一个循环,需要输出到结束符或者长度限制为止。
const answer = (input: Number[]): Number[] => { |
所以在模型内部,只要生成的下文还没有结束,它就必须保持一个内部状态(为什么?)。之前提到,语言模型是一个上下文概率模型,每一个字,都和他的上文有关系。在图片分类任务里,对一个图片分类了,就结束了。在给下一个图片分类的时候,上一个图片是什么类别已经毫无关系了。在下棋的例子中,由于每次生成最佳位置之后,是需要“执行”这一步下棋的,一旦棋子下了,也就确定了。但是在大语言模型例子里,只要回答的句子还没生成完,句子的每一个字,都和其上文有关,所以这个中间状态必须持续累积下去,直到句子生成完毕。
考虑以下例子:
上文:今天天气很好,
下文:我们去散步吧
假设我们给定上面的上文,大语言模型生成了下文,那么我们可以得到以下的生成序列,每一行是一个时刻的快照。
| 时刻 | 上文 | 下文 |
|---|---|---|
| \(t_0\) | 今天天气很好, | 我 |
| \(t_1\) | 今天天气很好,我 | 们 |
| \(t_2\) | 今天天气很好,我们 | 去 |
| \(t_3\) | 今天天气很好,我们去 | 散 |
| \(t_4\) | 今天天气很好,我们去散 | 步 |
| \(t_5\) | 今天天气很好,我们去散步 | 吧 |
| \(t_6\) | 今天天气很好,我们去散步吧 | END |
此时我们可以非常抽象地直接引入一个变量“当前状态”,用于描述模型处于该时刻的状态,那么可以得到下面的序列数据。
| 时刻(\(t\)) | 上文(\(x\)) | 状态(\(h\)) | 下文(\(y\)) |
|---|---|---|---|
| \(t_0\) | 今天天气很好, | \(h_0\) | 我 |
| \(t_1\) | 今天天气很好,我 | \(h_1\) | 们 |
| \(t_2\) | 今天天气很好,我们 | \(h_2\) | 去 |
| \(t_3\) | 今天天气很好,我们去 | \(h_3\) | 散 |
| \(t_4\) | 今天天气很好,我们去散 | \(h_4\) | 步 |
| \(t_5\) | 今天天气很好,我们去散步 | \(h_5\) | 吧 |
| \(t_6\) | 今天天气很好,我们去散步吧 | \(h_6\) | END |
这个“状态”,虽然是一个抽象的概念,但是它却是一个实质的东西,具体表示在 \(t_i\) 时刻模型的状态,其具体内容我们会在下面看到。(为了术语统一,这里使用 \(h\) 表示这个状态,在其他语料中,这个状态被称为隐藏状态(hidden state))
从上面的例子可以看出,整个时序的模型,被抽象为以下的流程。
\[ \text{Model}(x_t) \to (y_t, h_t) \]
而实际上,状态之间也存在依赖关系,所以每个时刻的输入,不仅仅只有该时刻的 \(x_t\),还需要以上一个时刻的状态作为参考。
\[ \text{Model}(x_t, h_{t-1}) \to (y_t, h_t) \]
这个将作为模型建模的重要基础之一。
(其实更精确的表达应该是\(\text{Model}_{h_t}(x_t, h_{t-1}) \to y_t\))
编码器-解码器架构
有了上面的基本关系,目标是如何得到 \(h_t\),以及 \(y_t\)?在基本模型看来,\(h_t\) 和 \(y_t\) 是同时产生的,他们是不是并列关系呢?其实还可以从另一个角度来看这个问题。我们把上面的时序数据表,看成以下的形式。
graph LR
t0[$t_0$] --> x0["今天天气很好,"]
x0 --> h0[$h_0$]
h0 --> y0["我"]
t1[$t_1$] --> x1["今天天气很好,我"]
x1 --> h1[$h_1$]
h1 --> y1["们"]
t2[$t_2$] --> x2["今天天气很好,我们"]
x2 --> h2[$h_2$]
h2 --> y2["去"]
如此类推。实际上图上的箭头表示一个“变换”,而一个变换无非就是一个函数,既然如此,我们也可以往里面插入一个抽象的函数来实现这个变换。
graph LR
t0[$t_0$] --> x0["encoder('今天天气很好,')"]
x0 --> h0[$h_0$]
h0 --> d0["decoder($h_0$)"]
d0 --> y0["我"]
t1[$t_1$] --> x1["encoder('今天天气很好,我', $h_0$)"]
x1 --> h1[$h_1$]
h1 --> d1["decoder($h_1$)"]
d1 --> y1["们"]
t2[$t_2$] --> x2["encoder('今天天气很好,我们', $h_1$)"]
x2 --> h2[$h_2$]
h2 --> d2["decoder($h_2$)"]
d2 --> y2["们"]
也就是说,我们通过对当前输入编码的方式,得到当前的一个隐藏状态,然后再通过解码的方式,把这个隐藏状态转化为输出。
\[ \begin{align*} &\text{encoder}(x_t, h_{t-1}) \to h_t \\ &\text{decoder}(h_t) \to y_t \end{align*} \]
上面的公式也可以直接整合为一个公式。
\[ \text{decoder}(\text{encoder}(x_t, h_{t-1})) \to y_t \]
而这个编码器解码器架构,一般就被称为 Transformer 架构。
\[ \begin{align*} &\text{transformer} = \text{decoder}.\text{encoder} \\ &\text{transformer}(x_t, h_{t-1}) \to y_t \end{align*} \]
其实从形式上说,上面的所有函数名,都是“抽象的”,而复合函数,本身也是一个函数,所以在这个架构里,我们可以只使用
encoder,也可以只使用
decoder,也可以同时使用。
\[ \begin{align*} &\text{encoder}(x_t, h_{t-1}) \to y_t \\ &\text{decoder}(x_t, h_{t-1}) \to y_t \\ &\text{transformer}(x_t, h_{t-1}) \to y_t \end{align*} \]
这里举一个例子方便理解编码器与解码器。
比如我们看到一个苹果,然后说出来“这是一个苹果”,这个过程实际上也是“编码-解码”的过程。
我们眼睛看到一个苹果,其实是看到很多维度的东西,比如这是一个类似于球体的东西,它的大小比我们手掌稍小,它是红色的,表面较为光滑。这些离散的信息进入大脑之后,会被整合(编码)为一个“隐含表示(隐藏状态)”,至于这个状态具体是什么,估计无人能说清楚,但必然会有这一个状态。然后我们通过知识对这个状态进行解码,我们就知道这个红红的表面光滑,比我们手掌稍微小一点的球体,是一个苹果。
另外还有一点可以注意到的是,这些隐藏状态是连续的。一个很好的例子是我们会认错人,我们通过人的特征进行编码,内化为一个隐藏状态,比如看到现在网红脸,她们特点都很类似,在我们心智里无法精确定位到某一个状态,所以我们看到的时候,无法立刻叫出那具体是谁,通常需要更多的额外信息帮助定位。
自注意力机制
从上面的讨论来看,在大语言模型的语境下,我们有了两个基本工具,一个是处理时序数据,一个是 Transformer 架构。但人们很早就发现上面的架构是有问题的,关键点在于隐藏状态,变相淹没了部分时序特征。
一个简单的数字例子
从一个简单的例子开始,假设我们有一个时序数据序列
[0, 3, 4, 2, 1] |
假设我们的隐藏空间大小是 \(1\),编码器是求和函数,那么我们有以下的时序数据表。
| 时刻(\(t\)) | 上文(\(x\)) | 状态(\(h\)) | 下文(\(y\)) |
|---|---|---|---|
| \(t_0\) | [0] | 0 | 3 |
| \(t_1\) | [0, 3] | 3 | 4 |
| \(t_2\) | [0, 3, 4] | 7 | 2 |
| \(t_3\) | [0, 3, 4, 2] | 9 | 1 |
| \(t_4\) | [0, 3, 4, 2, 1] | 10 | END |
从这个表来看,这个状态是一个数字,在任意时刻,这个数字表示前面出现过的数字之和,如果数字的出现顺序非常重要,那么这个”求和“动作实际上隐藏了数字顺序信息。
一个翻译例子
下面再来看一个稍微复杂一点点的例子。假设我们目前希望模型执行翻译任务(输入输出都是字符串)。
输入:Kannst du mir helfen diesen Satz zu übersetzen
输出:Can you help me to translate this sentence
由于英语是标准的 SVO 语言,而德语使用习惯中大部分时候用 SOV 语序,所以两种语言的语序是不同的。

如果按照上面提到的方式直接对输入句子进行编码解码,那将丢失语序信息。
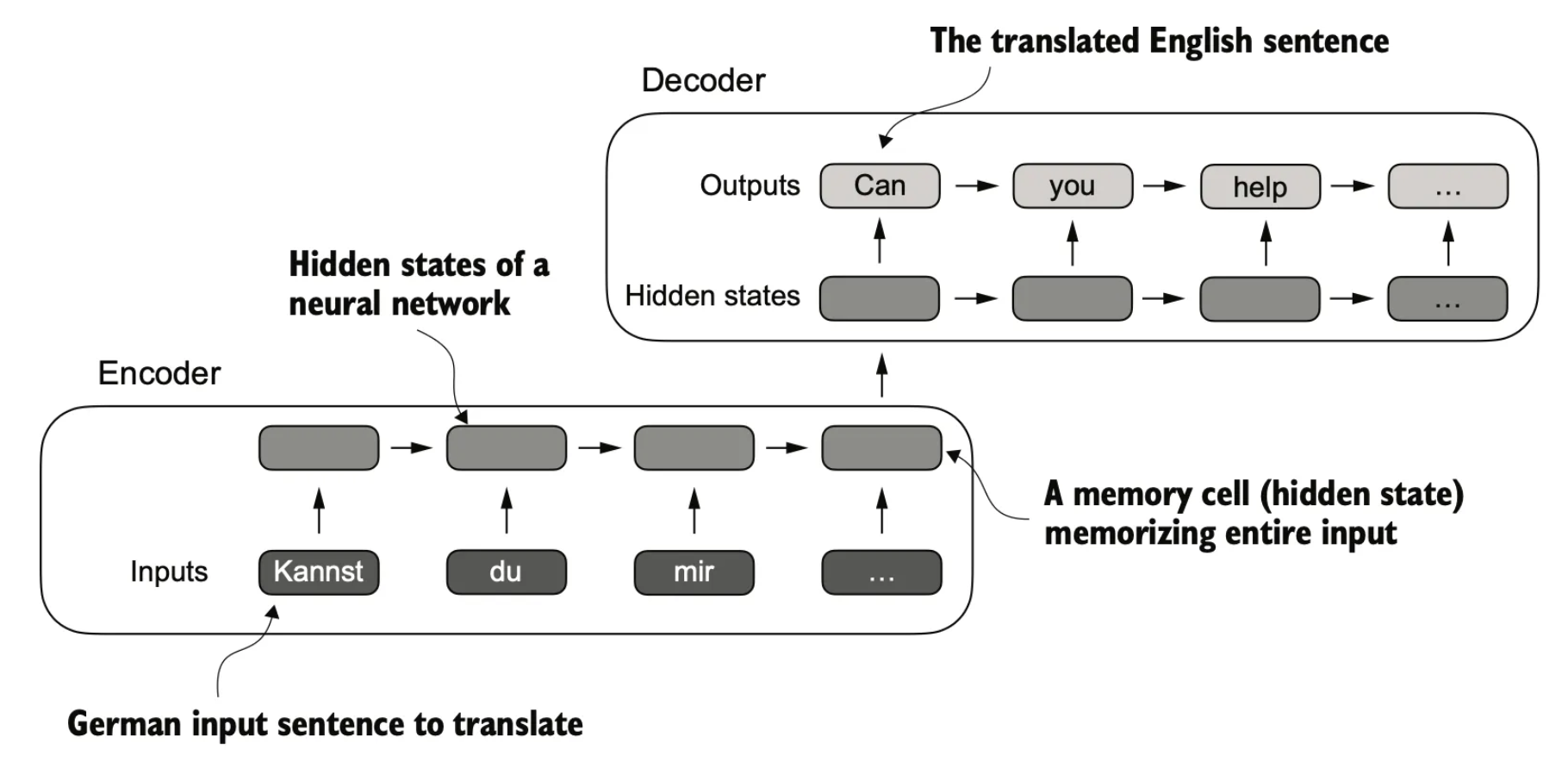
其实从对应关系中我们也可以看到,每个输入词,对于每个输出词来说,“重要程度”是不同的。如果我们不希望隐藏状态丢失信息,那么最暴力的解决办法就是“保留所有信息”。而保留所有信息的意思是,在每一个下文生成的时候,每一个上文都要参与到计算中。
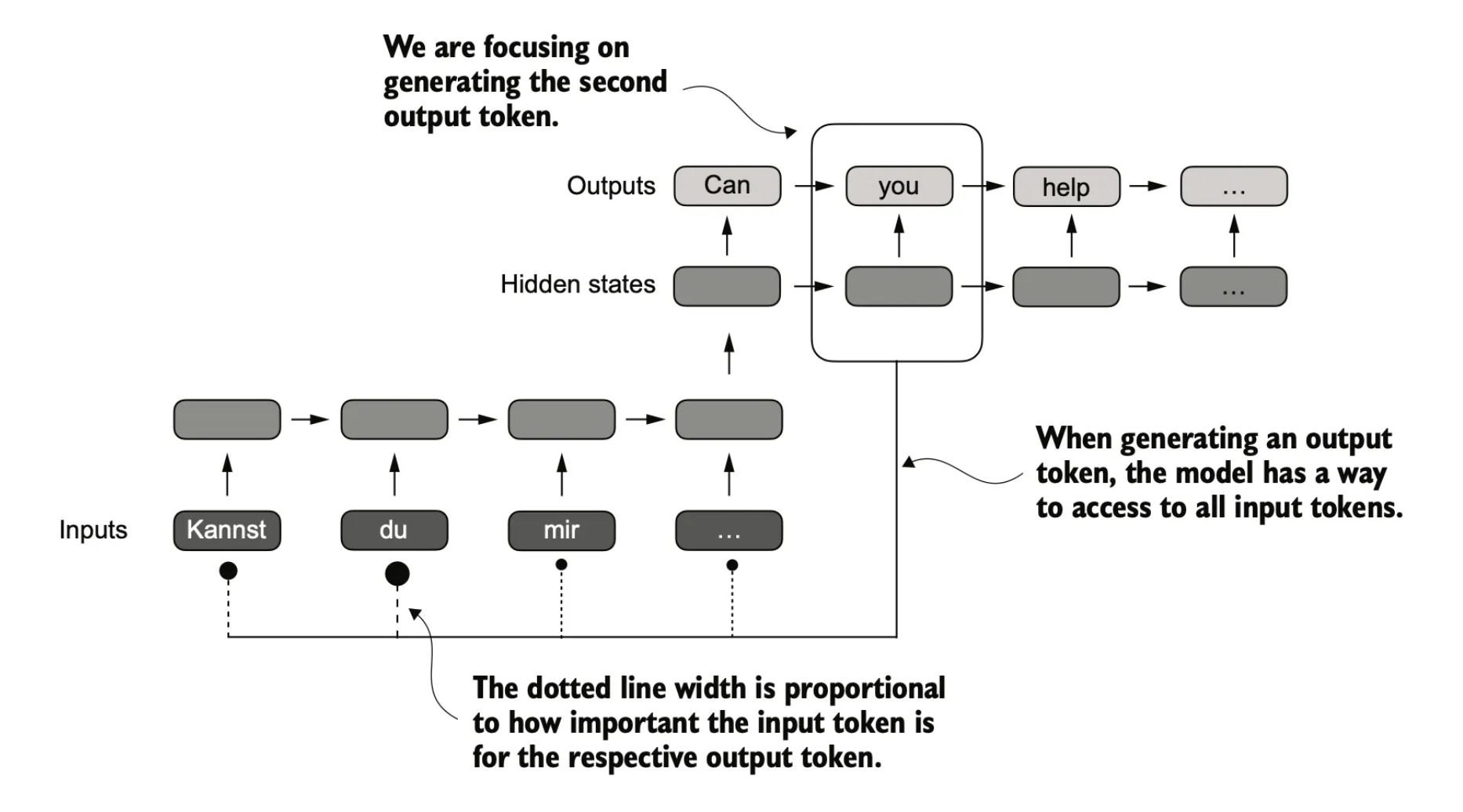
从上图可以看到,当生成“you”的时候,对于整个输入句子的单词都会参与计算,只是输入句子的不同单词影响程度会有所不同,而影响力最大的,肯定是“du”这个单词。
通过这个例子,我们可以感受到输入的时序信息对输出是有非常大的影响的。而自注意力机制,就是指这种每一个输出都需要每一个输入参与计算的机制。
小结
- 时序数据:对于大语言模型来说,输入的句子,是一个时序输入。
- 隐藏状态:隐藏状态是大语言模型在处理完一次输入之前,任意时刻的内部状态。
- Transformer架构:编码-解码架构,将输入编码成隐藏状态,然后再从隐藏状态解码为输出。
- 自注意力机制:由于隐藏状态会丢失时序信息,所以自注意力机制让输出的每一个单词都注意输入的每一个单词。