AI学习时间 04 - 训练
#训练 #损失 #批学习
#学习率 #大模型预训练
复习
训练:通过不断地尝试,来得到模型的参数。
graph LR Data[训练数据] --> Model[模型] Model --> Output[模型输出] Target[期望输出] --> Loss[损失函数] Output --> Loss Loss --> Optimizer[优化器] Optimizer -->|更新参数| Model数据集:包含了我们希望模型学习的样本。
损失函数:接受模型的输出和我们期望的输出,然后输出一个损失值。
优化器:接受损失函数的输出,然后输出一个新的模型。
大模型:一个将输入转换为输出的函数,本质是一系列向量变换的组合
const output = Model(input)
大语言模型:是概率模型,预测给定上下文的下一个词,条件概率表示为 \(p(w_1, \dots, w_m) = \prod^m_{t = 1} P(w_t | w_1, \dots, w_{t - 1})\)。
训练
对于一个模型的训练,是寻找最优的参数的过程,使得模型的输出尽可能接近我们期望的输出。下面是模型训练的一次循环。
const model = new Model() |
在这个流程中有几个关键问题:
- 损失是如何衡量的?
- 模型的参数是怎样更新的?
一个简单的例子
数据集
假设现在有这些数据,我们需要找到一个模型,使得
- 这个模型能尽可能拟合这些已知数据
- 这个模型能比较好预测未来的数据
目标函数
从这个简单的数据集,我们可以看到这些数据点“貌似”是在一条直线上的。当然,事先知道这个答案可能会对我们的理解更有利。这个目标函数是 \(y = 2x\)。
建模与误差
假设我们事先不知道这个答案是 \(y = 2x\),我们也不能对问题一无所知,通过数据猜测(或者说建立)背后的模型,也是需要一定的洞察力和方法的,但我们先跳过这个“建模”的技巧说明,先聚焦于深度学习训练这个课题。假设我们已经有一定的洞察力了,知道这是一条直线(为了让说明更简单,这里先忽略直线不过原点的情况),那么我们就得到了一个简单的模型:
\[ y = ax \]
我们先对 \(a\) 值进行一个盲猜,假设我们猜 \(a = 1\),那么模型与数据之间就会产生误差,我们通过一个整体误差来衡量这个猜测。
上图展示的虚线长度(一般为了方便是用长度的平方)总和就是 \(a = 1\) 时模型产生的整体误差,也可以形式化表示为
\[ \text{loss} = \sum_{i=1}^n \big[y_i^\text{data} - y_i^\text{model(a=1)}\big]^2 \]
由于我们知道答案,所以可以想一个办法让 \(a\) 慢慢靠近正确答案 \(a = 2\),但是作为一个通用的方法,我们需要有一种通用的方式来更新参数。观察上面的公式,里面的两个变量
- \(y^\text{data}_i\) 是已知的数据
- \(y^\text{model}_i\) 是模型的输出,也就是 \(f(x^\text{data}_i) = a x^\text{data}_i\)
整个公式里,只有 \(a\)
一个未知变量,所以当整体误差展开的时候,是一个一元二次方程,并且二次项符号是正的。由于上标均变为
data,所以下面省略上标。
\[ \begin{align*} \text{loss} &= \sum_{i=1}^n \big[y_i - ax_i\big]^2 \\ &= \sum_{i=1}^n \big[y_i^2 + ax_i^2 - 2 a y_i x_i\big] \\ &= \sum_{i=1}^n y_i^2 + \sum_{i=1}^n a^2 x_i^2 - \sum_{i=1}^n 2 a x_i y_i \\ &= + \color{blue}\sum_{i=1}^n x_i^2 \color{black} a^2 - \color{blue}\sum_{i=1}^n 2 x_i y_i \color{black} a + \color{blue}\sum_{i=1}^n y_i^2 \\ \end{align*} \]
既然是一个一元二次方程,开口向上,那么它就会存在一个最低点,因为我们知道正确答案是 \(a=2\),所以这个抛物线的顶点,就是在 \((2, 0)\) 这个位置。
损失函数与学习
上述讨论还揭示了一点,不知不觉间,我们发现整体损失 \(\text{loss}\) 实际上是关于模型参数 \(a\) 的一个函数 \(\text{loss} = f(a)\),这意味着,当我们通过调整 \(a\) 让 \(\text{loss}\) 达到最小值,那么此时的 \(a\) 就是我们需要的模型参数了。
有了上面的认知与工具,我们就可以开始考虑如何更新参数了。在上面的例子中,我们一开始猜测 \(a = 1\),此时我们得到一个误差,但此时并没有任何信息告诉我们,应该往哪个方向调整 \(a\) 的值,究竟是尝试 \(a = 1.5\) 还是 \(a = 0.5\)(假设更新步长是 \(0.5\))。此时我们可以不用决策,随机找一个方向即可,通过误差的变化来指导下一步的操作。
从上图我们可以看到,当 \(a\) 变大到 \(1.5\) 的时候,整体误差变小了,所以这个方向是正确的,于是我们可以继续往这个方向调整。如果我们固定步长是 \(0.5\) 的话,那么下一个迭代就会到 \(a = 2\),这样我们就能终止整个更新过程。
考虑到方向性的问题,如果我们要判断方向,是需要一些“标记”的,观察这个典型的抛物线图,往上误差增大,往下误差减小,当从一个位置向上下移动的时候,刚好可以通过符号来判断。
导数就是用来衡量这种变化的一种方式,回顾一下对于一元二次方程的导数,是以下的形式
\[ \begin{align*} y &= ax^2 + bx + c \\ y' &= 2ax + b \end{align*} \]
对于上面的损失函数来说,我们把 \(y_i = 2x_i\) 也代入,会得到
\[ \begin{align*} \text{loss} &= \sum_{i=1}^n \big[y_i - ax_i\big]^2 \\ &= \sum_{i=1}^n \big[2x_i - ax_i\big]^2 \\ &= \sum_{i=1}^n x_i^2 a^2 - \sum_{i=1}^n 4 x_i^2 a + \sum_{i=1}^n y_i^2 \\ \frac{\partial \text{loss}}{\partial a} &= 2\sum_{i=1}^n x_i^2 a - 4\sum_{i=1}^n x_i^2 \\ &= 2Ca - 4C \text{(把常数换为} C \text{)} \end{align*} \]
从这个公式可以看到,当 \(a = 2\) 的时候,导数为 0,也就是这个点是这个函数的极值点,也就是我们需要的最小值。
但假设我们将这个抛物线看成是一个现实中的斜坡,那参数更新的过程可以看成是从某一个位置释放一个小球,这个小球会随着重力的作用往下滚动,如果这个斜坡还是有阻尼的话,那么这个小球最终会停下来,也就是这个参数更新最终会使得误差为 0,当然,这是非常理想的情况。但可以想象到的是,通过这种方式,是可以找到最优解的。
上面展示的是另一种更新的可能,虽然看着在最优值之间来回跳动,但是只要向着损失最小化的方向,最终还是有机会到达最优点。
学习率与参数更新
进一步看,\(a\) 在抛物线两边变动的时候,导数的变动方向刚好和误差的变动方向是一致的(大家可以验证下),而误差是 \(a\) 的函数 \(\text{loss} = f(a)\),对这个函数求导,实际上表明了 \(a\) 的变化会如何导致误差的变化,这两者的变化是同步的。而我们的目标是让误差最小,所以可以通过导数反过来指导 \(a\) 的变化。
这意味着 \(a\) 的更新可以写成(注意符号,导数为正意味着误差增大,我们要往反方向走,所以是减去导数,如果导数是负数,意味着误差减小,方向正确,所以负负得正)
\[ a \gets a - \text{loss}' \]
理论上这个公式就可以作为参数的更新方式了,但是考虑到误差的导数是不可控的,如果我们希望控制更新的步长,此时我们需要引入一个学习率(learning rate)的参数,用来“限制”变动的比例。
\[ a \gets a - \color{blue}\eta \color{black}\text{loss}' \]
直观上看,抛物线越往上越陡峭,如果我们学习率为 \(1\),也就是不控制步长的话,\(a\) 的变动会非常大,有可能直接错过最优解,而越靠近最优解,坡度越平缓,如果步长足够小,那么可以很有机会慢慢接近最优解。
小批量学习
在上面的例子中,我们是使用一堆数据点的误差总和进行学习的,这其实已经属于批量学习(batch learning)的范畴。先考虑一下,一个个点进行学习会产生什么问题。
从上图可以看到,过一点其实会有无数条直线,这意味着过这一点能够找到无数个函数,使得误差为 \(0\),这相当于我们的模型可以有无数个解,以至于无法学习。但当我们选取一小部分的点一起训练,情况就不同了。
从上图可以看到,如果是一次计算几个点的误差,那么这几个点到红色直线(目标函数)的损失为 \(0\),而这几个点到绿色和蓝色直线的误差都比较大,所以如果我们的建模“比较准确”的话,通过几个点一起训练可以大大增加学习的准确率。
大语言模型的预训练
语言模型的内在逻辑是概率模型,也就是给定一个上文,得到一个下文的概率分布。大语言模型的预训练,就是为了学习这个概率分布。而这个概率分布的目的,是为了预测下一个词。
通过上面的例子,我们已经知道一个训练过程的关键要点,接下来我们可以逐个环节来看大语言模型是如何训练的。
数据集
在上面的例子中,由于输入和输出都是数字,然后模型是一个简单的线性函数,所以我们很容易理解这些数字和函数在后面的流程是如何被使用的,到了大语言模型这个语境里,输入 \(x\) 是什么?输出 \(y\) 又是什么?
直观来看,由于大语言模型是用来预测下一个词的,那么“下一个词”,自然就是我们所希望的 \(y\),而它的上文,就是对应的 \(x\)。假如我们有这样一个语料(这个语料很简陋,只有一句话)。
今天天气很好
那么我们可以构造以下数据。
| data ID | \(x\) | \(y\) |
|---|---|---|
| d0 | BEGIN | 今 |
| d1 | 今 | 天 |
| d2 | 今天 | 天 |
| d3 | 今天天 | 气 |
| d4 | 今天天气 | 很 |
| d5 | 今天天气很 | 好 |
| d6 | 今天天气很好 | END |
这种构造数据的方法,称为自监督的预训练。因为全程无需人类标注,只需要有语料库,就能通过字符串处理构造出一堆的原始训练数据,所以称为自监督。当然,实际的切割方法还有不少讲究的地方,但是暂时不深入过多,需要稍微注意的一点是,让大模型学会何时终止也是非常重要的,所以在句末需要加上一个特别的占位符
END。(句首同理)。
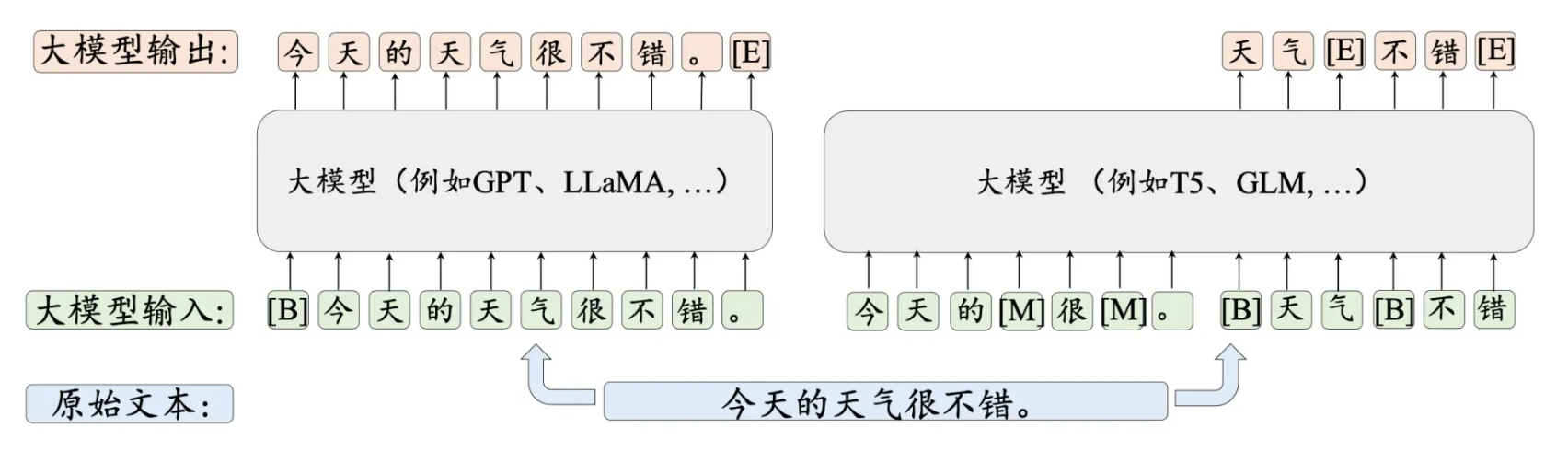
上图也展示了另一种构造数据的方式,通过对一个句子进行挖空,然后让大模型来填空,注意挖空处的标记。这种挖空的训练任务称为去噪自编码。
建模
给大语言模型建模,当然不是一件简单的事情。下面是目前主流的基于 transformer 架构的大语言模型架构图。这样图比较出名,大家可能不止一次看到过。

这个架构后面会详细解释,相信到时候大家也会明白为什么是这样的设计,以及里面的细节与原理,不过现在暂时不深入,因为并不影响理解,这个复杂的架构,与上面例子里的 \(y = f(x) = ax\) 并没有本质的区别,这个架构无非就是多了很多层的函数以及循环而已。
但这个图值得我们注意的一点是,最后的输出是输出概率。
损失
在上面的例子里,由于输出是一个数值,而数据里也是数值,所以我们可以很直观地使用两者之间的距离作为损失的衡量。但大模型最后一步输出的是一个概率分布,那该如何拿这个概率分布,与我们期望的概率分布进行对比并计算损失呢?
假设上图是“今天天气很”的大语言模型输出,在这个上文下,理论上“好”的概率应该是最高的,因为这句话和其他几个字都不太搭,但大模型却给出了“天”是最高概率,这与我们的期望是不一致的。而且从上面的数据中,d5
这个数据(['今天天气很', '好'])的答案也是“好”,所以我们需要一种方法来描述这种认知差别,也就是我们希望的分布应该是这样的。
数学上有一种叫做交叉熵(cross entropy)误差的方法用于描述两个概率分布之间的差异,计算方式为
\[ E = -\sum_{w \in \mathcal{V}}^n p(w) \log q(w) \]
其中 \(p\) 是我们期望的概率分布,\(q\) 是大模型输出的概率分布,\(n\) 是概率分布的维度(在这个例子中就是词汇表单词的数量)。通过这种方式,我们也将误差转化为一个数值了,就可以用上面的老办法来进行训练了。
小结
- 训练:训练是寻找让误差最小的一组参数的过程。
- 数据集:数据集给出一组输入输出,让模型通过学习来得到一组参数。
- 损失:损失是模型参数的函数,用来衡量当前模型的参数造成的整体误差。
- 学习率:可以通过对损失函数求导来更新参数,但是通常会乘以一个比率来控制参数变化粒度。
- 大语言模型预训练:采用一种自监督的学习方式来学习语言模型。
- 预训练数据:通过构造上下文的方式来构造训练数据。
- 交叉熵误差:用来衡量两个概率分布之间的差异。