光线追踪初步

发表于 2024-11-09 分类于 Computer Disqus：本文字数： 4.6k 阅读时长 ≈ 17 分钟

本文主要讲述光线追踪最基础的部分，包括整个思路的各个组成部分以及基本原理。为了略去不必要的细节，本文的伪代码基本采用 ts 语法。需要查阅细节的话，可以自行搜索，各种光线追踪教材里面都包含非常多的细节。

综述

光线追踪是一种计算机图形学技术，用于模拟光在场景中的传播和交互。它通过追踪光线的路径来生成逼真的图像。下面是常见的使用场景：

渲染真实感图像：光线追踪可以生成高度逼真的图像，包括光照、阴影、反射和折射效果。
电影和动画制作：许多电影和动画制作公司使用光线追踪来创建逼真的特效和场景。
游戏开发：光线追踪在游戏开发中越来越受欢迎，用于实现更真实的光照和阴影效果。

光线追踪可以算是一种离线算法，因为其巨大的计算量，并不适合实时计算（至少在我目前看到的来说）这意味着光线追踪产生的结果是一张图片。而不像其他实时算法一样，计算得到的是某个时刻的世界的信息（比如物体位置，运动速度，光线颜色等）。

而要得到一张图片，无疑需要确定这张图片每个像素的颜色，“光线追踪”得名于对光线的追踪，像素的颜色实际上是某一条光线经过各种反射，折射等运动与变换，最终击中这个像素点，那么我们沿着这条光线反向追踪，通过综合这条光线经过的各种环境与材质参与的颜色混合，得到其最终颜色，而这个颜色就是这个像素点的颜色。

通过对击中各个像素点的光线进行追踪，计算其颜色，就得到最终产物的产物。这个过程可以使用如下的伪代码表示。

const render = (width: number, height: number) => {
    const image = new Image()
    
    // 逐行循环
    for (let row = 0; row < height; row++) {
        // 逐列循环
        for (let col = 0; col < width; col++) {
            // 当前需要渲染的像素
            const pixel = new Vector2(row, col)
            // 计算从 origin 到该像素世界坐标的光线
            const ray = getRay(pixel)
            // 计算光线的颜色
            const color = getColor(ray)
            // 设置颜色
            image.setColor(pixel, color)
        }
    }
    
    return image
}

从上面的主要流程可以看到，光线追踪的核心逻辑是获取光线的颜色，整个流程最关键只有两步：

获取光线
获取光线的颜色

下面详细阐述如何获取光线，以及如何获取光线的颜色。而整个光线追踪的学问，可以说均包含在这两个步骤当中，对立面各个环节的细节进行不同的设计和考虑，就得到不同的渲染结果。

获取光线

渲染模型

从高层次来看，产物得到的图片，是对世界某一个瞬间的记录，对于静态环境来说，这个瞬间实际上就是光线的集合在一个平面上的体现。

对于人眼来说，这个“平面”是我们的眼睛，眼球上满布的视锥细胞将光转化为颜色。对于相机来说，这个“平面”是成像平面，对于旧式相机来说，光的信息留存在了胶片上。

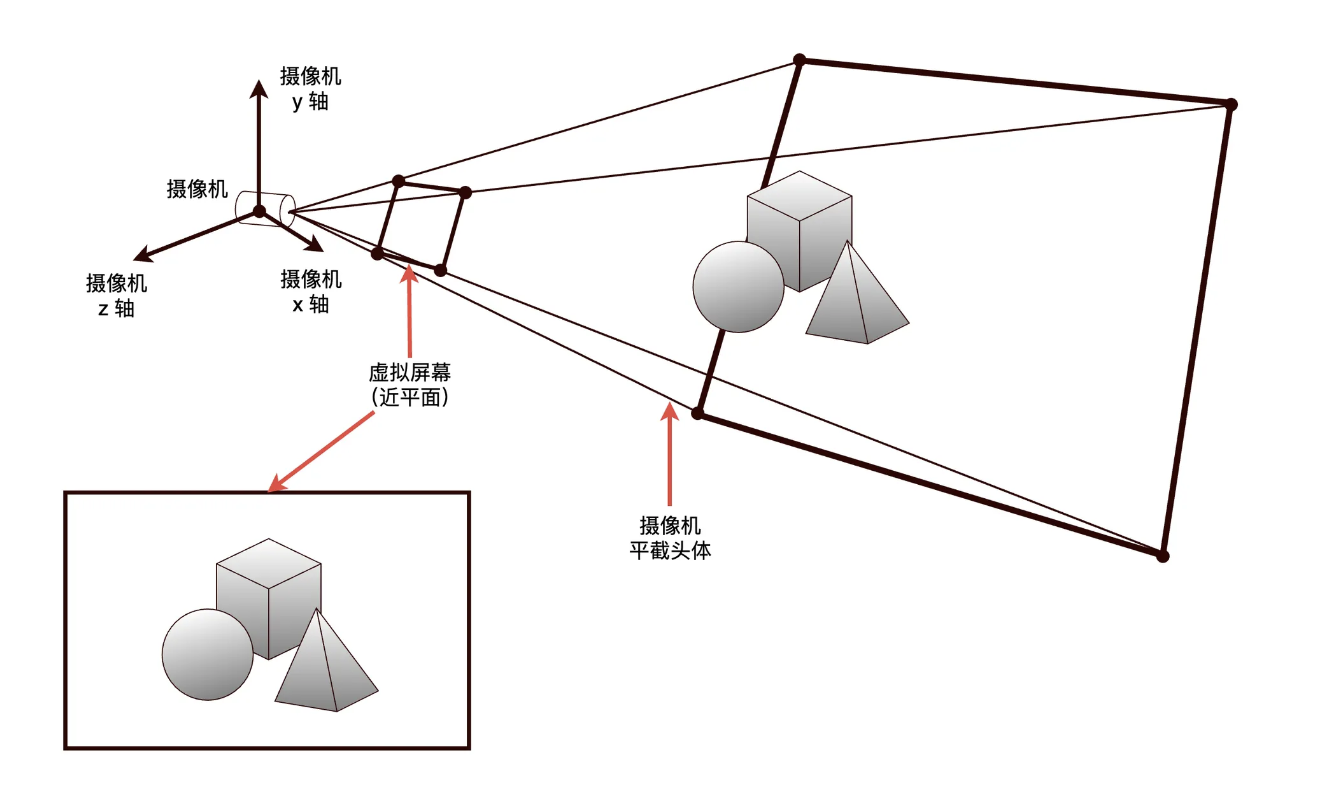
几乎所有三维计算机图形技术，在高层次来看都会使用这种渲染方法

上图展示了一个高层次的渲染模型，左下方是产物图片。图片的每一个像素颜色，均来源于世界的物体。

而这个世界物体的颜色，则来源于光线。

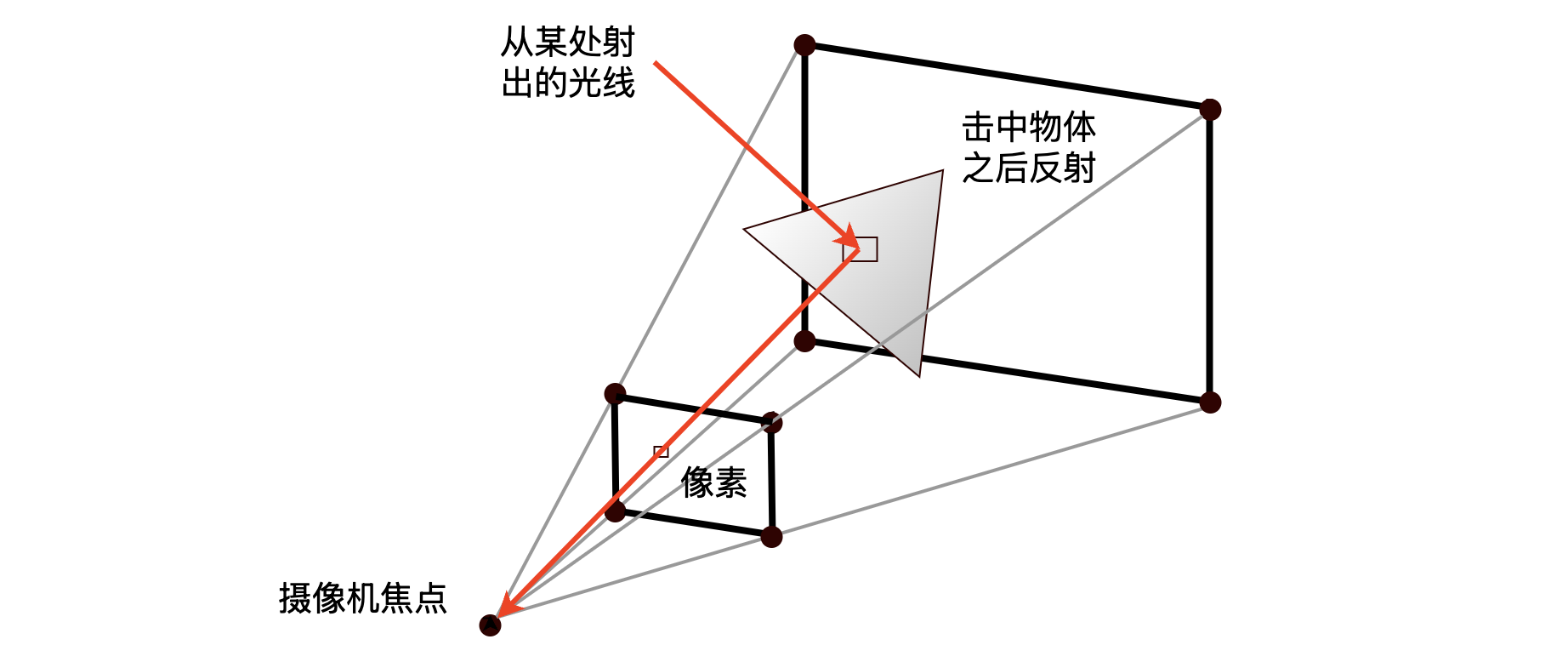
这个很容易理解，回想中学时代的物理，我们看到的物体的颜色，实际上是光射向物体之后反射进入我们眼睛的颜色，简单来说，这个颜色就是由物体的表面性质决定的。不过实际上情况会复杂很多，因为光经过各种反射会有能量损耗，在不同物体表面反射的时候也有不同的行为。

但由于我们主流程是渲染一张图片，逐行逐列地确定每个像素的颜色，所以实际上我们是在追踪这些入射光线。

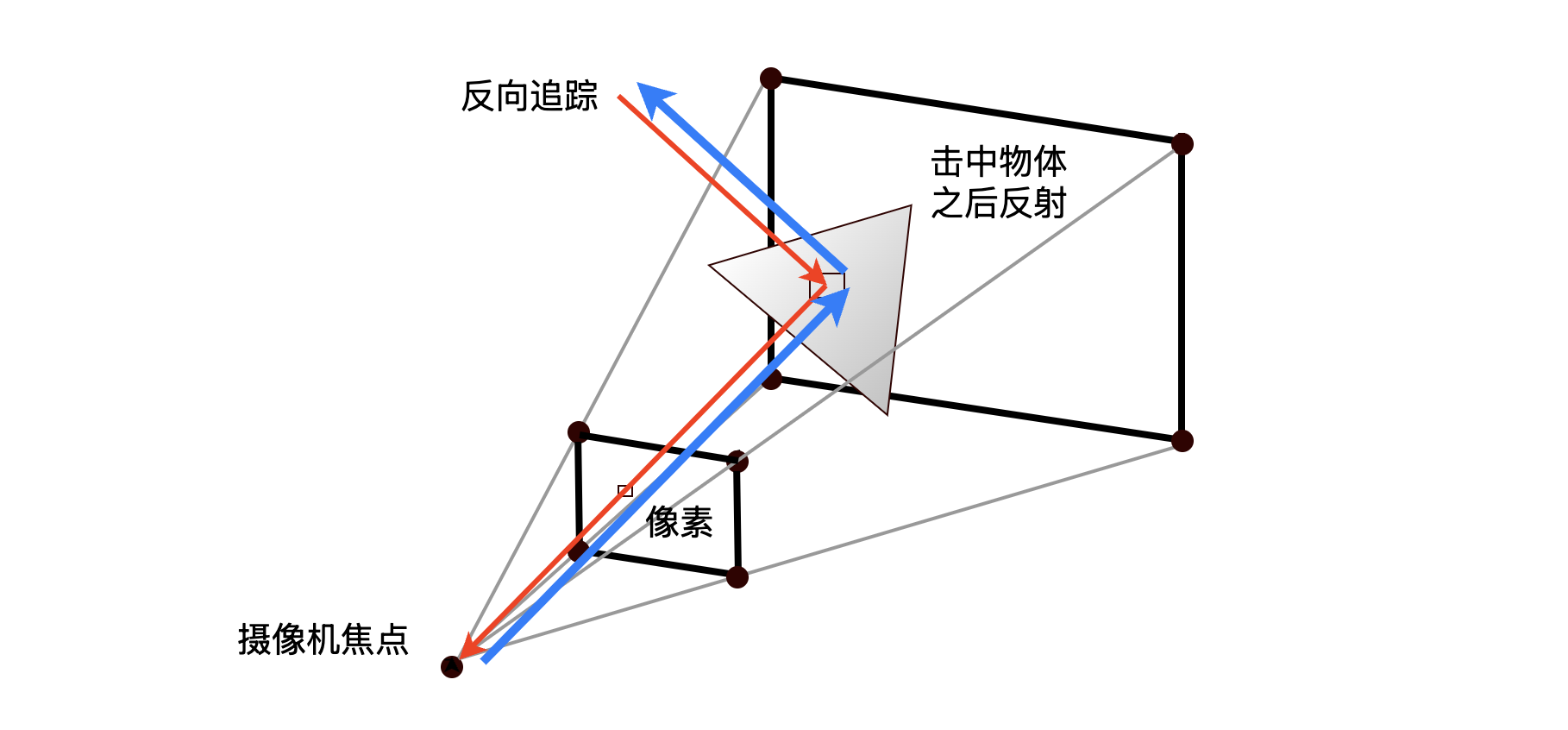
所以第一步我们先要计算从摄像机焦点发出的射向某一个像素点的光线方程。

相机几何

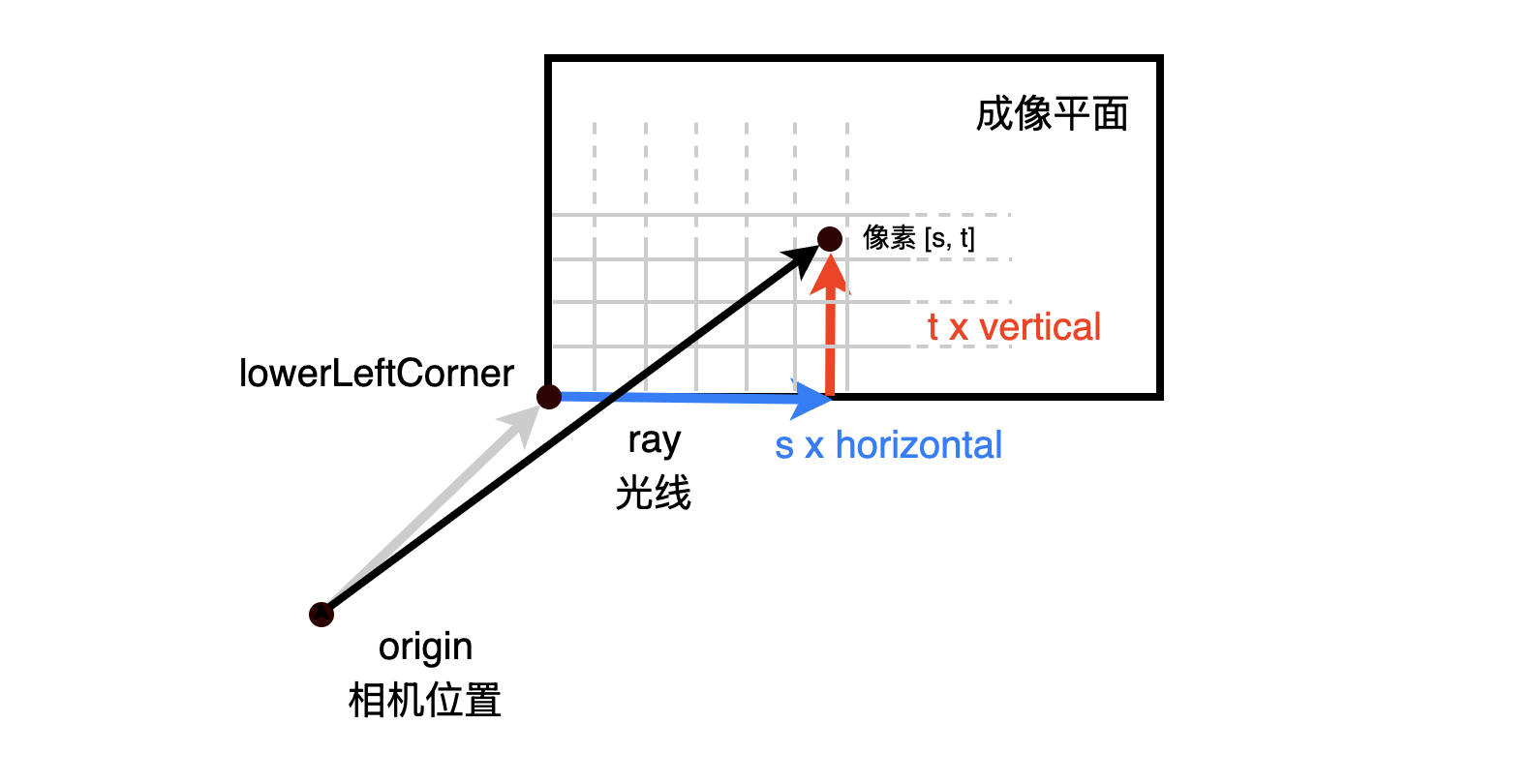
如上所述，相机几何处理的问题是计算“相机射向成像平面某一个像素的光线”，由于对于成像平面来说，我们是一个个像素点来反向追踪光线的，所以只要我们知道成像平面左下角（理论上可以选择其他点，选左下角只是一个习惯性约定）的坐标，这样我们通过加上实际像素对应成像平面左下角的偏移，来得到射向该像素的光线。

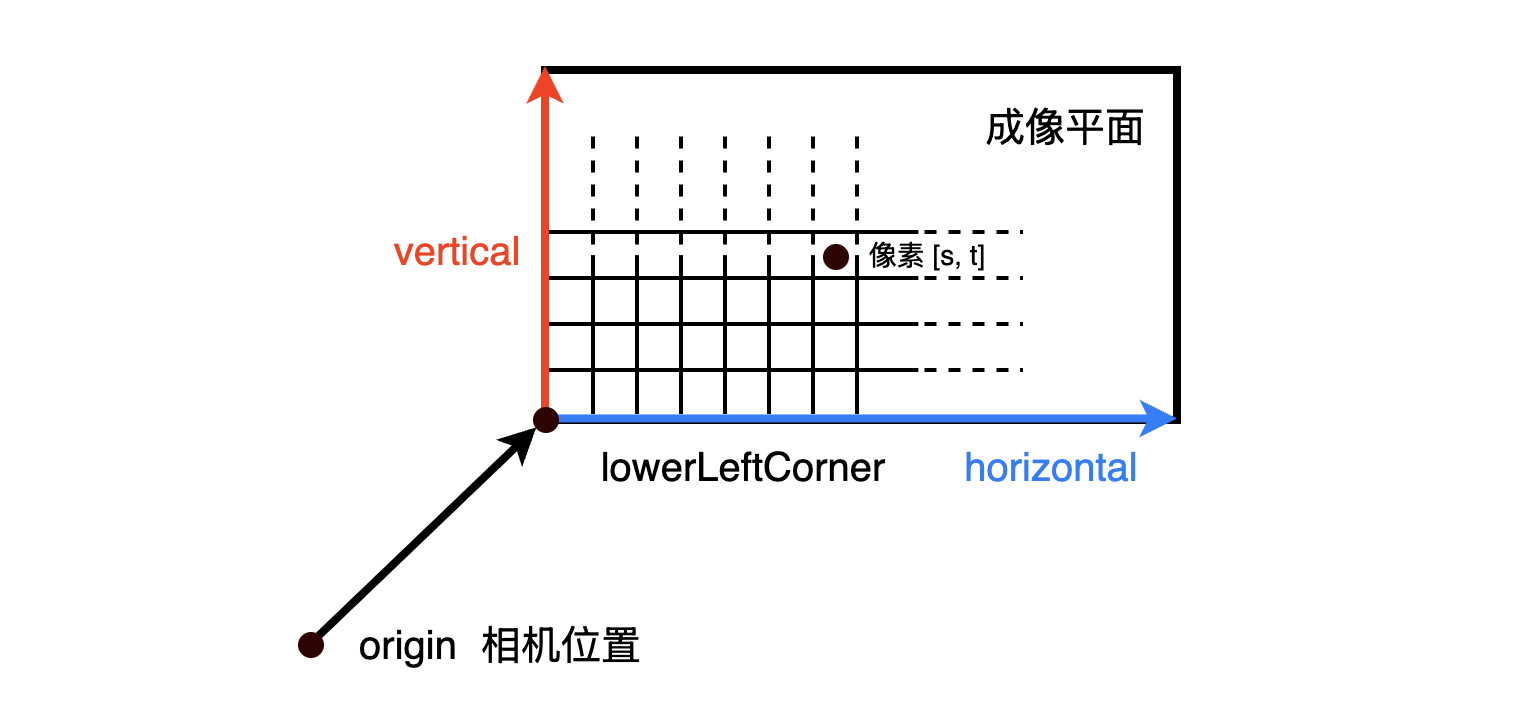
相机变量

由上面的讨论可以得到相机需要记录以下参数。

origin ：相机位置
lowerLeftCorner ：成像平面左下角坐标
horizontal ：成像平面水平向量
vertical ：成像平面竖直向量

有了这些变量，我们可以简单计算这条射向某个像素的光线。为了方便扩展，像素坐标不用整数 \([x, y]\) 来表示，而是使用水平偏移量百分比 \(s\) 与竖直方向便宜百分比 \(t\) 来表示，这样成像平面中心表示为 \([0.5, 0.5]\)。

相机参数

上面的相机变量是跟相机相关的位置参数，而相机还有另一组参数，更像是相机的固有属性，比如相机的广角大小，比如相机成像平面的长宽比等，相机变量实际上是需要依赖这些参数计算出来的。

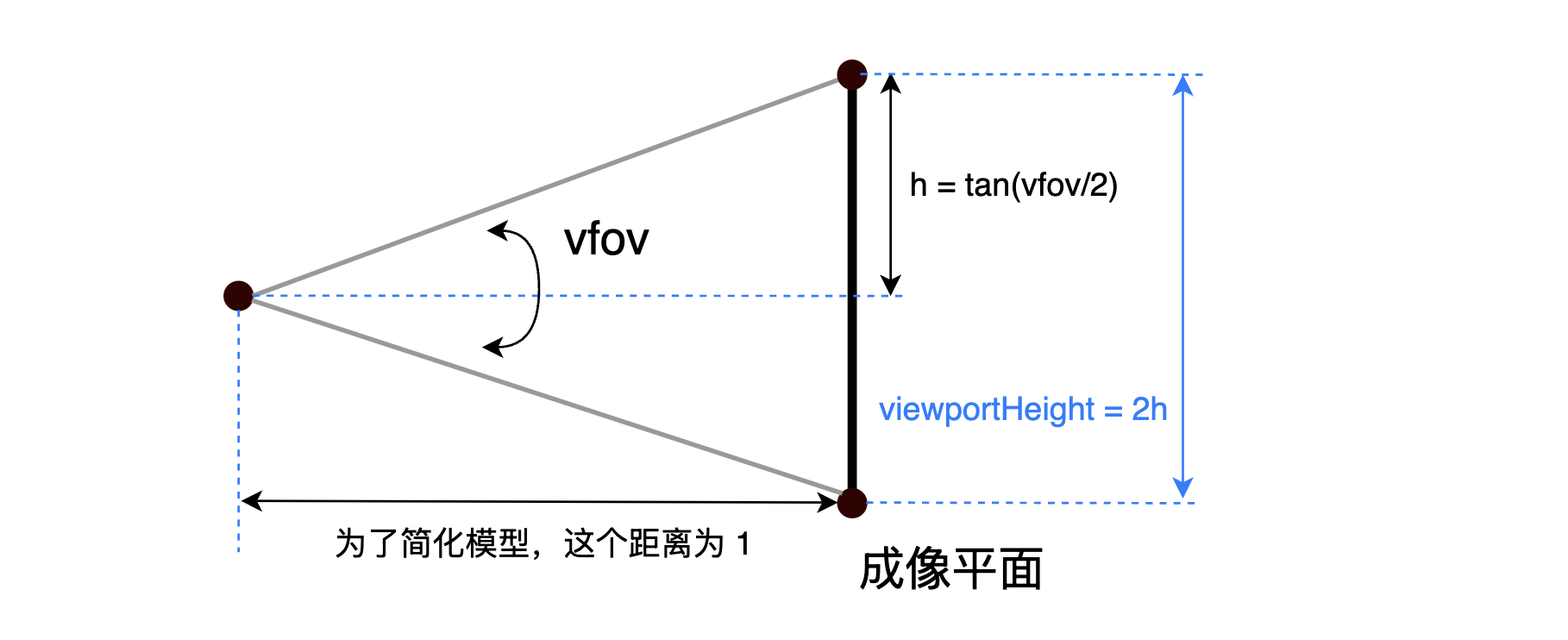
为了简化模型，将相机焦点与成像平面之间的距离设置为 1，也就是焦距为 1，这个值可以是任意值，对应的计算发生相应变化即可。由上图可以计算出成像平面的高度，再乘以成像平面宽高比 aspectRatio，则可以得到成像平面的宽度。

由于相机是可以任意转向的，所以必须把相机位置，相机朝向统一考虑，才能计算成像平面左下角的坐标。

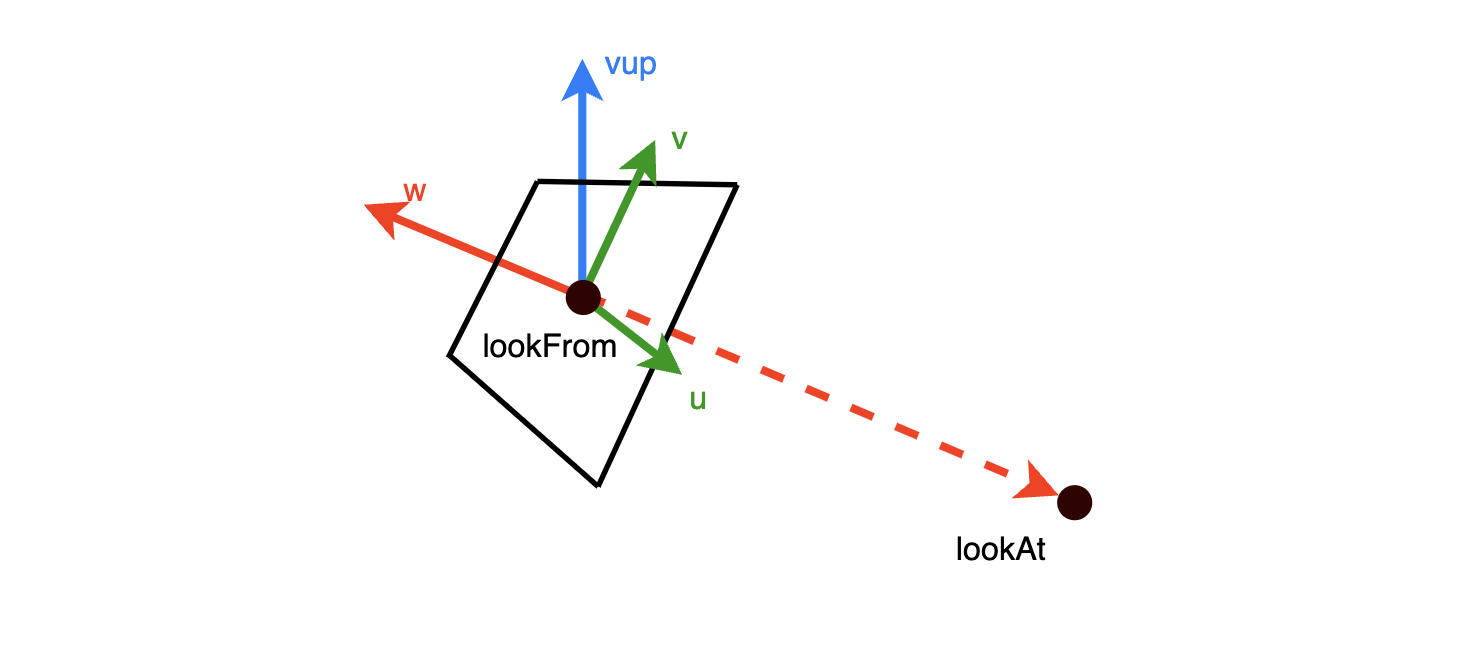
观察上图，lookFrom 是相机位置，lookAt 是照相机向着的物体位置。\(w\) 是相机朝向方向的反方向，\(vup\) 是竖直向上的方向。可以通过叉乘得到与两个向量垂直的向量，为了计算方便，另 \(w, v, u\) 都是单位向量，于是有

\[ \begin{align*} u &= \text{unitVector}( w \times vup )\\ v &= \text{unitVector}(w \times u) \end{align*} \]

由此得到下面的伪代码。

class Camera {
    origin: Point3;
    lowerLeftCorner: Point3;
    horizontal: Vector3;
    vertical: Vector3;
    
    constructor(
        lookFrom: Point3,
        lookAt: Point3,
        vup: Vector3,
        vfov: number, // vertical field-of-view in degrees
        aspectRatio: number
    ) {
        const theta = degreesToRadians(vfov);
        const h = tan(theta/2);
        const viewportHeight = 2.0 * h;
        const viewportWidth = aspectRatio * viewportHeight;
        
        const w = unitVector(lookFrom - lookAt);
        const u = unitVector(cross(vup, w));
        const v = cross(w, u);
        
        this.origin = lookFrom;
        this.horizontal = viewportWidth * u;
        this.vertical = viewportHeight * v;
        this.lowerLeftCorner = origin - horizontal/2 - vertical/2 - w;
    }
}

发射光线

有了相机几何基础，我们就可以从相机向屏幕的某个像素点发射一条光线。

class Camera {
    const getRay(s: number, t: number): Ray => {
        return new Ray(
            this.origin,
            this.lowerLeftCorner
                + s*this.horizontal
                + t*this.vertical
                - this.origin    
        )
    }
}

获取光线颜色

要确定像素的颜色，实际上是反向追踪从相机发出的光线，观察其击中的物体（或者无击中）的性质，累积这些性质对光线产生的影响，从而得到光线最终到达成像平面的颜色。在初中物理中，我们知道太阳光是可以分解为不同的颜色，我们也知道光的三原色，白色的太阳光照射到物体上，有部分光被吸收，部分被反射或者折射，所以在光传播的过程中，每击中一个物体，其能量就会减弱，被反射或者折射的光继续传播，然后击中下一个物体，如此重复，直到击中相机的成像平面。

所以需要获取光线的颜色，有两部分需要计算

光线的传播行为：慢反射，镜面反射，折射，能量衰减…
可击中的物体及其材质：漫反射材质，镜面反射材质，折射材质…

光线的传播行为

越真实的物理效果，会使用更多样的光线传播方式，会采用更精确的更符合物理规律的方式计算，比如将光视作光谱，一个连续的波。不过本文作为光线追踪的初步，只将光视作一种颜色，一个 \([r, g, b]\) 三元组。

光传播的时候是一个递归过程，从发射点开始，击中物体，然后改变方向继续传播，然后击中物体，最后反向到达光源。

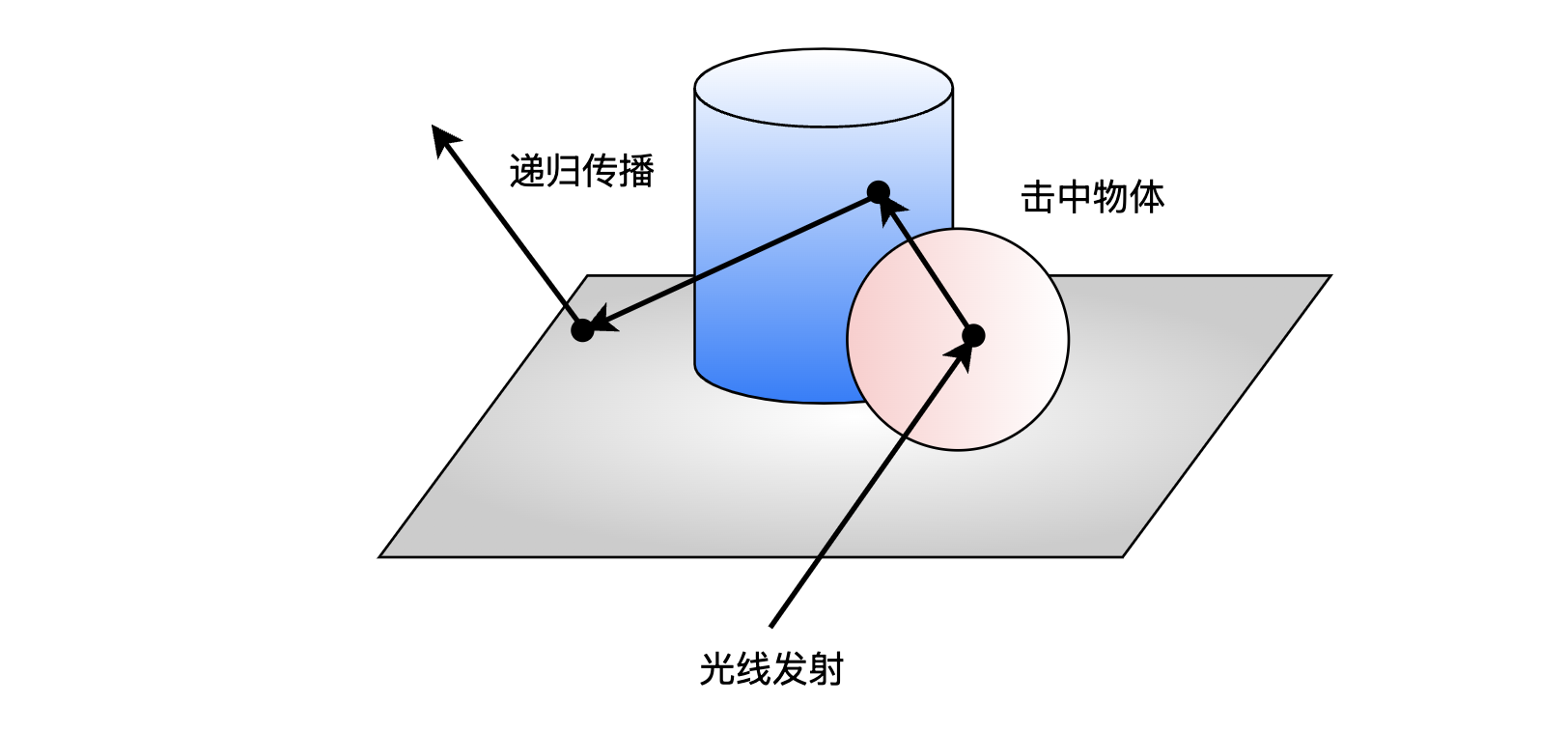
我们先定义一个击中记录结构，用于记录击中点的性质。

interface HitRecord {
    p: Point;           // 击中点
  normal: Vector3;    // 击中点的表面法向量
  t: number;          // 光线参数方程的解
  material: Material; // 击中点所在物体的材质
  frontFace: boolean; // 击中点的表面是否向着光来的方向
}

整个反射的递归过程可以描述如下

const rayColor = (ray: Ray, world: Hittable, depth: number) => {
    // 递归达到最大深度限制，就返回黑色
    if (depth <= 0) return new Color(0, 0, 0)
    
    // 计算光线能击中的最近的物体
    const hitRecord: HitRecord = world.hit(ray, 0.001, Infinity)
    
    // 如果有击中，计算散射光线
    if (hitRecord) {
        const {
            scatterd as Ray, 
            attenuation as Color,
        } = hitRecord.material.scatter(ray, hitRecord)
        
      // 如果有散射（漫反射，镜面反射，折射）
        if (scattered && attenuation) {
            // 递归调用（不断传播）
            return attenuation * rayColor(scattered, world, depth - 1)
        }
        
        return Color(0, 0, 0)
    }
    
    // 没击中任何物体，返回背景色
    return backgroundColor
}

漫反射

日常中看到的大部分物体都是漫反射物体，这类物体表面是粗糙的，不透明的，我们看到它们的颜色，是由它们反射最多的光来确定的。

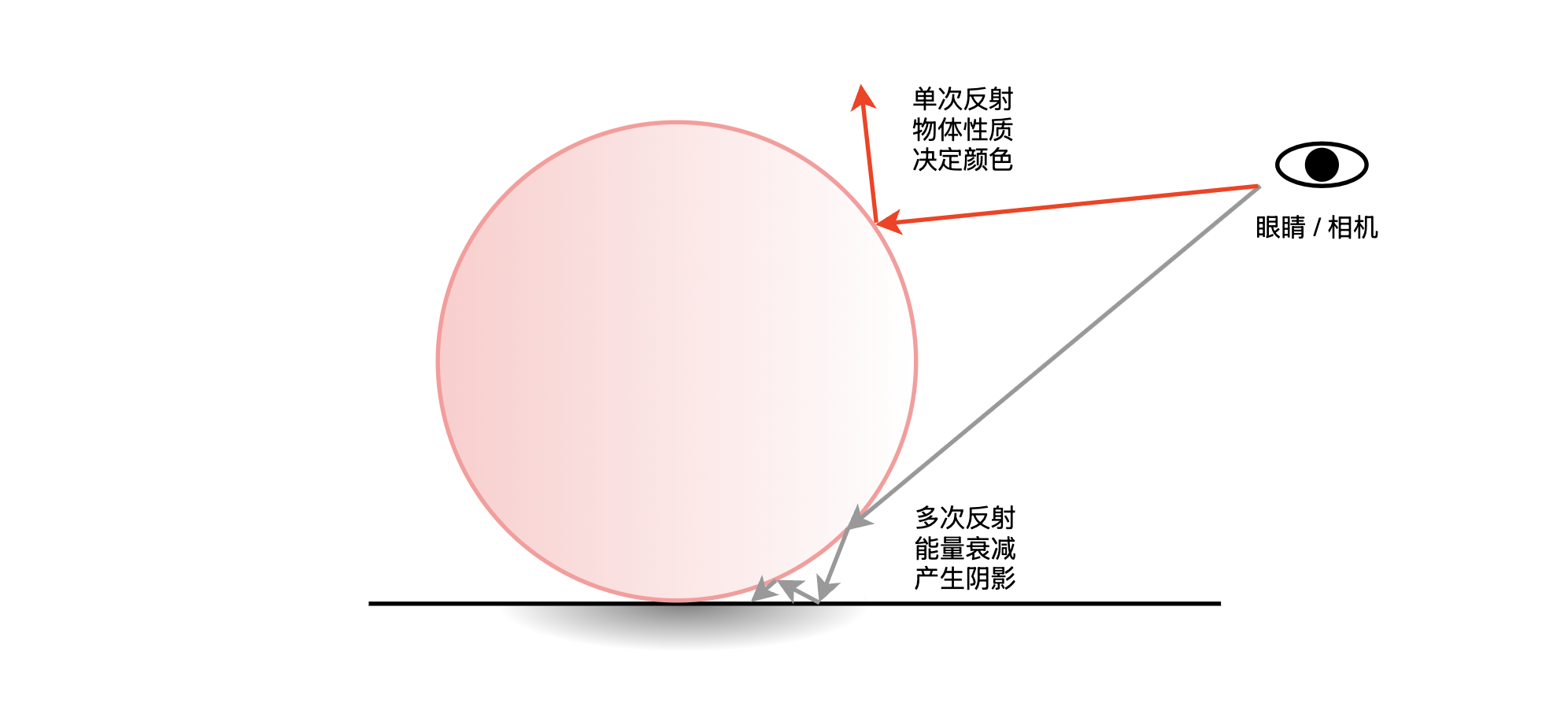
上图是慢反射示意图。我们看到一个慢反射物体的颜色，是由其反射的最多的光的颜色来决定的，比如一个红色的球，那意味着这个球反射最多的是红光。

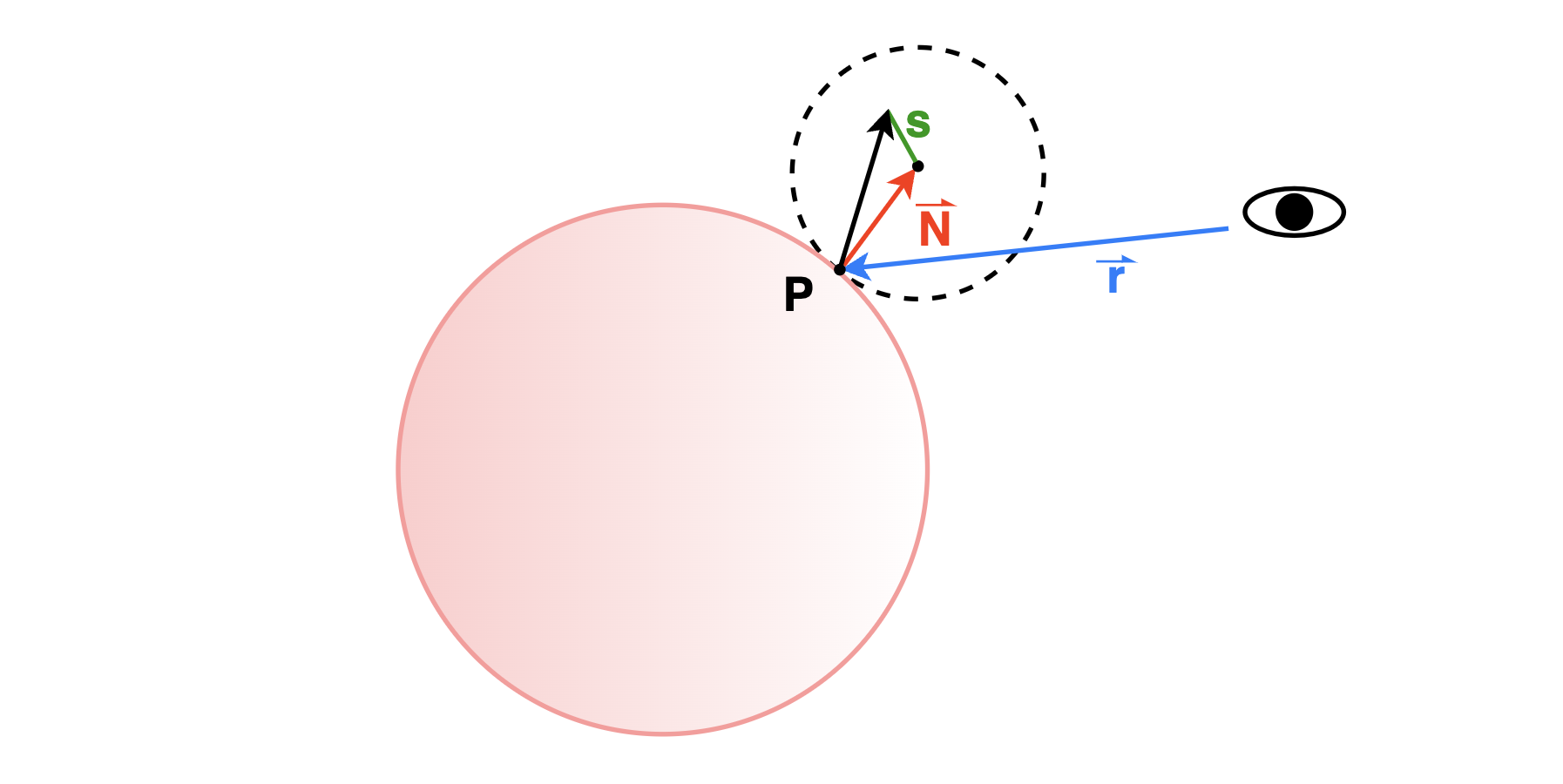
在漫反射中，为了模拟物体凹凸不平的样子，光线不会严格遵循入射角等于反射角，而是进行一个微小程度的随机。上图中入射光线是 \(\textbf{r}\)，击中点的法向量是 \(\textbf{N}\)，为了模拟这个微小的随机，在单位圆内随机生成一个小向量 \(\textbf{s}\)，这样反射光线方程如下

\[ \textbf{r'} = \color{blue}\textbf{r} \color{black} + \textbf{P} + \color{red}\textbf{N} \color{black}+ \color{green}\textbf{s} \]

代码实现如下

const scatter = (r: Ray, hitRecord: HitRecord) => {
    // 漫散射光线
    const scattered = r + hitRecord.p + hitRecord.normal + randomVectorInSphere()
    // 物体颜色（红色）
    const color = new Color(255, 0, 0)
    
    return {
        scattered,
        attenuation: color,
    }
}

得到的效果如下图所示

镜面反射

在镜面反射里，光线完全遵从入射角等于反射角。

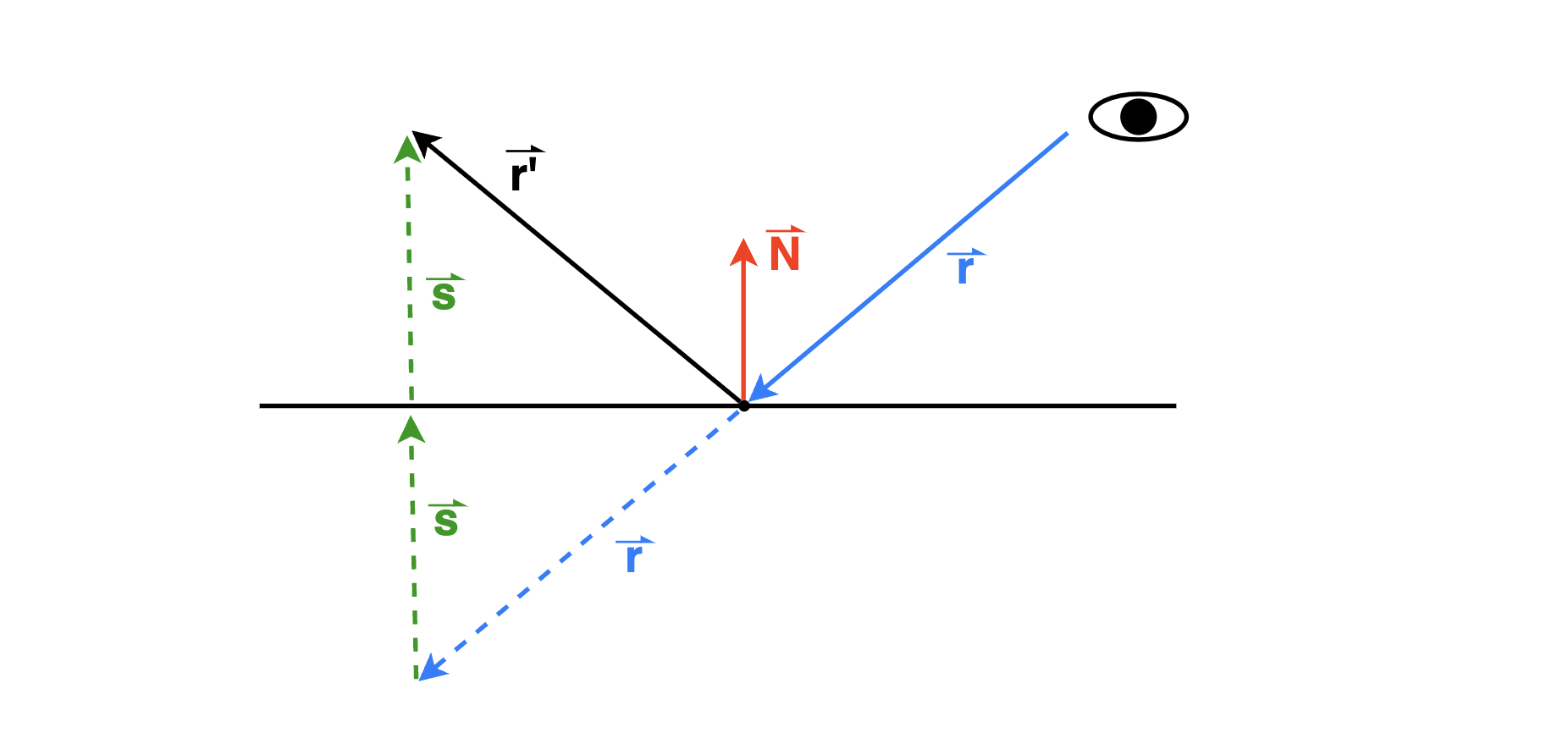
上面是一个镜面反射的示意图，其中 \(\textbf{s}\) 的方向与击中点的法向量 \(\textbf{N}\) 方向相同，其值为入射光线 \(\textbf{r}\) 在 \(\textbf{N}\) 方向上的投影，通过点乘可以算出。由此得到反射光线的方程为

\[ \begin{align*} \textbf{r'} &= \color{blue}\textbf{r} \color{black} + 2 \color{green}\textbf{s} \\ &= \color{blue}\textbf{r} \color{black} + 2 |\color{blue}\textbf{r} \color{black} \cdot \color{red}\textbf{N} \color{black}| \color{red}\textbf{N} \end{align*} \]

代码实现如下

const scatter = (r: Ray, hitRecord: HitRecord) => {
  const N = hitRecord.normal
    // 镜面反射光线
    const scattered = r + 2 * dot(r, N) * N 
    // 物体颜色（红色）
    const color = new Color(255, 0, 0)
    
    return {
        scattered,
        attenuation: color,
    }
}

得到的效果如下图所示

折射

对于绝缘体，比如水，比如空气来说，会发生折射现象。光线射向这些绝缘体，会直接穿透，并且改变一定角度继续前进，这个改变的角度遵循 Snell 定理。

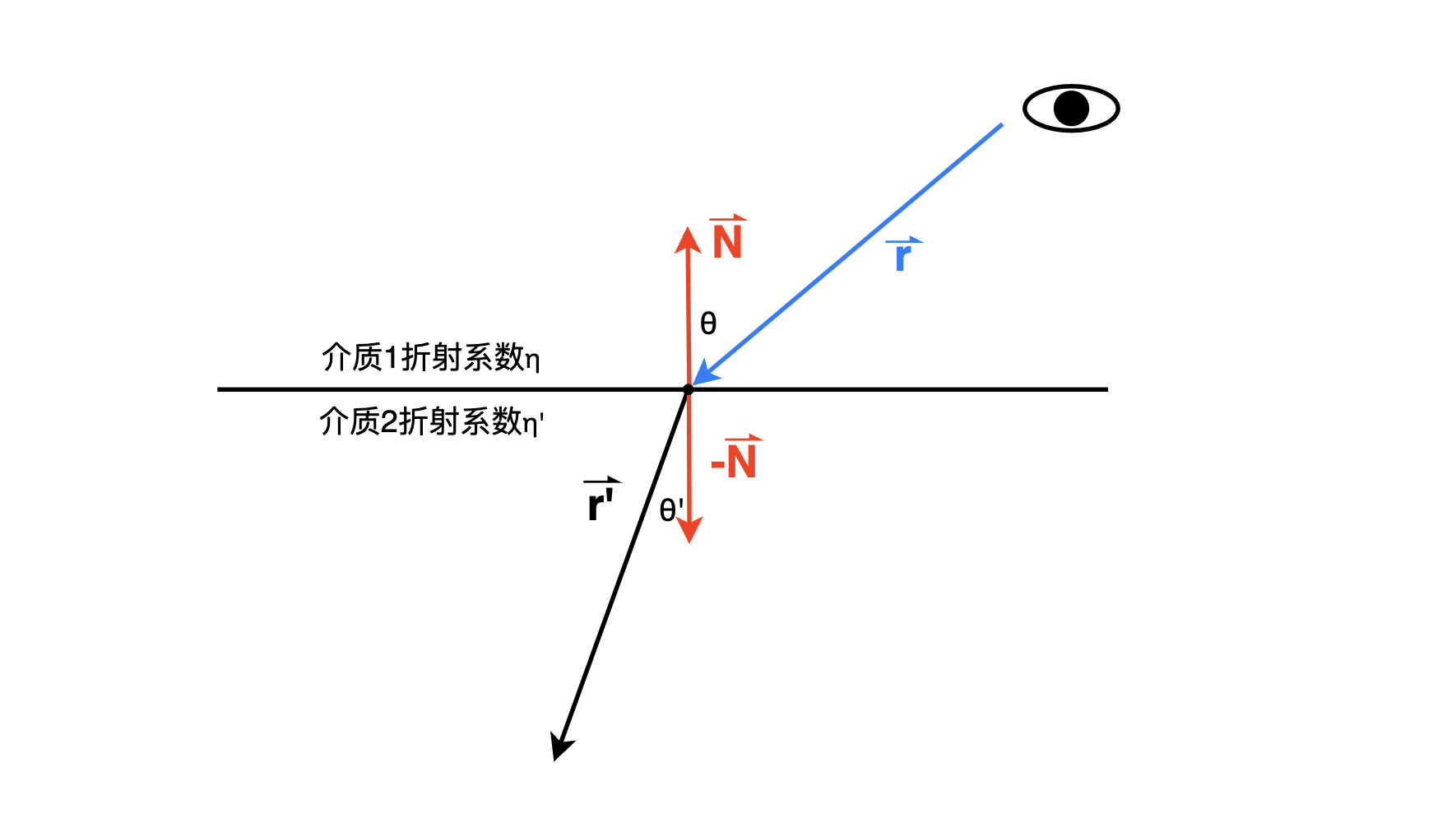
Snell 定理如下

\[ \eta \cdot \sin \theta = \eta' \cdot \sin \theta ' \]

为了得到折射光线的方向，我们要计算 \(\theta'\)

\[ \sin \theta' = \frac{\eta}{\eta'} \cdot \sin \theta \]

在折射侧，令折射光线为 \(\textbf{R}'\)，法向量为 \(\textbf{n}'\)，它们之间的夹角为 \(\theta'\)，我们可以在法向量平衡，以及法向量垂直两个方向对 \(\textbf{R}'\) 进行分解，得到

\[ \textbf{R}' = \textbf{R}'_{\perp} + \textbf{R}'_{\sinhortparallel} \]

解一下方程可得

\[ \begin{align*} \textbf{R}'_{\perp} &= \frac{\eta}{\eta'}(\textbf{R} + \cos \theta \textbf{n}) \\ \textbf{R}'_\sinhortparallel &= -\sqrt{1 - |\textbf{R}'_\perp|^2 \textbf{n}} \end{align*} \]

上式的未知数为 \(\cos \theta\)，由余弦定理可知 \(\textbf{a} \cdot \textbf{b} = |\textbf{a}||\textbf{b}| \cos \theta\)，如果两个向量都是单位向量，那么 \(\textbf{a} \cdot \textbf{b} = \cos \theta\) 。于是可以将 \(\textbf{R}'_\perp\) 写为

\[ \textbf{R}'_\perp = \frac{\eta}{\eta'}(\textbf{R} + (-\textbf{R} \cdot \textbf{n}) \textbf{n}) \]

下面是代码实现

const scatter = (r: Ray, hitRecord: HitRecord) => {
  const N = hitRecord.normal
  const n = N.normalize()
  const uv = r.normalize()
  const cosTheta = dot(-uv, n)
  
    // 折射光线垂直分量
    const rPerp = etaRatio * (uv + cosTheta * n)
    // 折射光线平行分量
    const rParallel = -Math.sqrt(1 - rPerp.lengthSquared() * n)
    // 折射光线
    const scattered = rPerp + rParallel
    
    // 折射不衰减，也就是不带上自己的颜色（透明）
    const color = new Color(1, 1, 1)
    
    return {
        scattered,
        attenuation: color,
    }
}

得到的效果如下图所示

可击中物体及其材质

在上面光的传播一节里，已经给出了如何递归地“回溯”光线的流程，里面涉及到一个比较重要的步骤 world.hit，这个步骤是为了找到射出的光是否击中物体，以及击中点的具体信息，而击中点的信息则是上面定义的 HitRecord 结构，里面记录了击中点的位置，法向量，击中物的材质等。所以整个步骤的关键在于，如何找到击中的物体，以及计算击中点的位置。

可击中集合

从一个简单而抽象的思维考虑这个问题，可以将世界看成一组可击中的物体，然后每个物体都可以单独计算是否被击中，当然，物体也是可以嵌套的，这样我们可以得到下面朴素的实现。

class Hittables {
    objects: Hittable[] = [];
    
    hit(ray: Ray, tMin: number, tMax: number) {
        const hitRecord: HitRecord
        const hitAnything: boolean = false
        const closestSoFar = tMax
        
        // 逐个物体进行碰撞检测
        _.each(this.objects, object => {
            const {
                hitAnything: hasHitSomething,
                hitRecord: record,
            } = object.hit(ray, tMin, closestSoFar))
            
            // 如果和某个物体发生了碰撞，记录碰撞信息
            if (hasHitSomething) {
                hitAnything = true
                closestSoFar = record.t
                hitRecord = record
            }
        })
        
        return { hitAnything, hitRecord }
    }
}

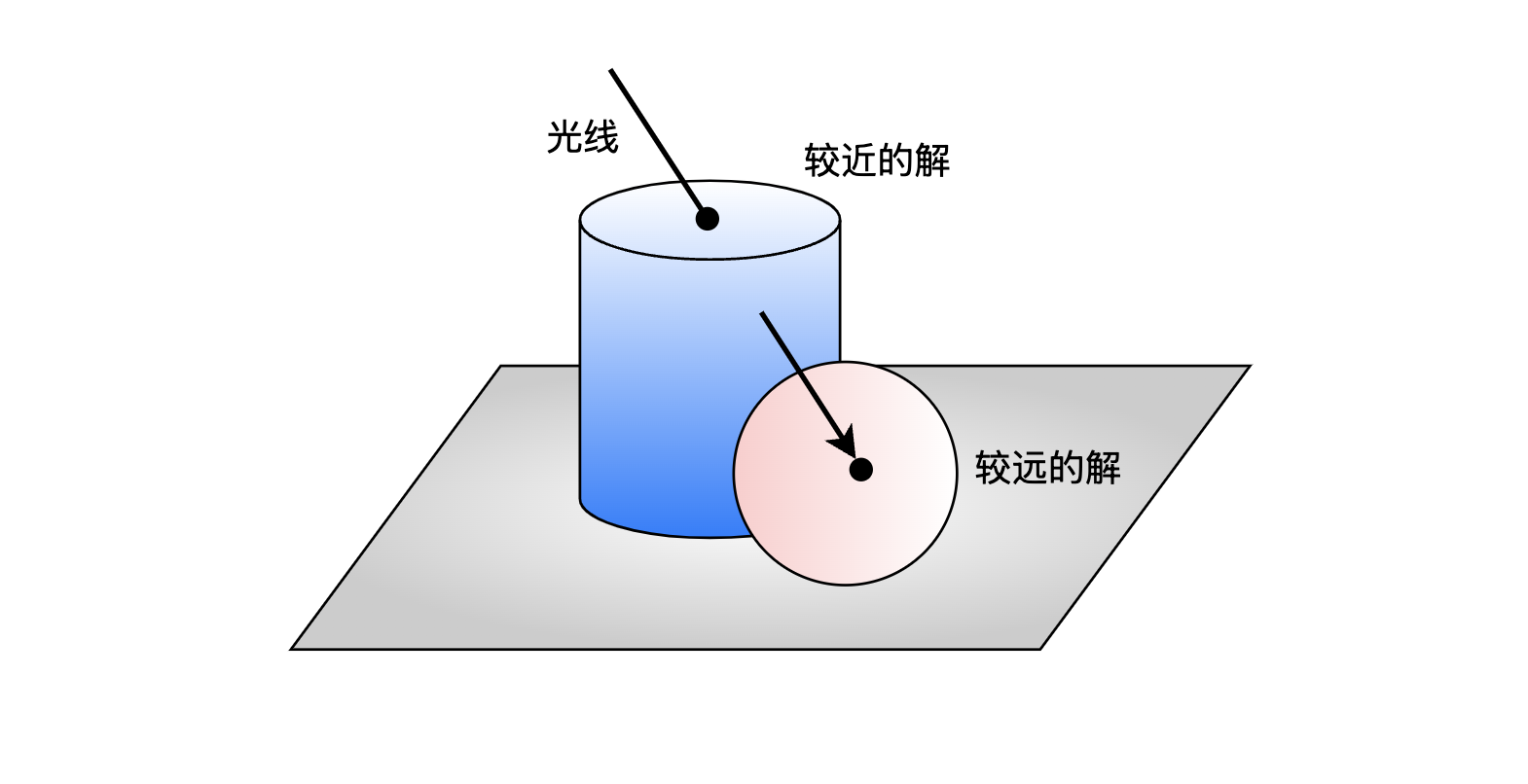
需要注意到的是，每次碰撞检测之后，会记录解 record.t ，并且将这个解当做是目前“最大的解”，从而看后面是否还存在比这个最大的解更小的解，因为目标是找到最近的击中对象。

可击中物体

在上面的代码里，对于每个物体来说，需要自行判断射过来的光线是否击中了自己，也就是 object.hit 方法，从这个角度来说，代码是很通用的。可以向世界添加各种各样的物体，只要这些物体提供 hit 方法即可。

所以我们可以实现各种可击中物体，比如球体，比如立方体，比如复杂模型。对于这些物体来说，击中方法的实现可能如下

球体：求解射线与球的交点，可以直接解方程获得，但是需要判断解是否在 \([t_\text{min}, t_\text{max}]\) 内
立方体：求解射线与立方体的交点与球体无异
复杂模型：对于复杂模型来说，模型是由一堆三角形组成，判断光线是否与模型相交，等于判断光线是否与模型里面的某个（某些）三角形相交

这实际上是碰撞检测的领域，碰撞检测一般分为两个阶段

宏观阶段：判断粗粒度结构是否相交（判断光线与子空间，或者包围盒是否相交）
微观阶段：判断细粒度是否相交，并且求解（判断光线是否与物体的某个面相交）

由于这不属于光线追踪的范畴，在此略过。

物体的材质

材质是物体的属性之一，在物体进行碰撞检测的时候，如果存在击中以及有合理解，那么物体的材质会记录在击中记录里。下面是物体（可击中物体）的定义。

class Hittable {
    material: Material
    
    hit(ray: Ray, tMin: number, tMax: number) {
        const hitRecord: HitRecord
        const hitAnything: boolean = false
        
        // 求解过程
        const t = Solve(this, ray)
        
        // 无击中
        if (t < tMin || t > tMax) return { hitAnything: false }
        
        // 击中
        hitRecord.p = ray.at(t) // 击中点
        hitRecord.normal = this.calculateNormal(hitRecord.p) // 计算击中点法向量
        hitRecord.material = this.material // 记录材质信息
    }
}

注意到，材质信息实际上是击中之后赋值到击中记录里的，这个材质信息会在计算光的后续光线 scattered 的时候用到，具体可以参见“光的传播行为”一节。

整体架构

上面介绍了光线追踪基本流程的所有要素。下面给出整个光线追踪流程的宏观架构图。

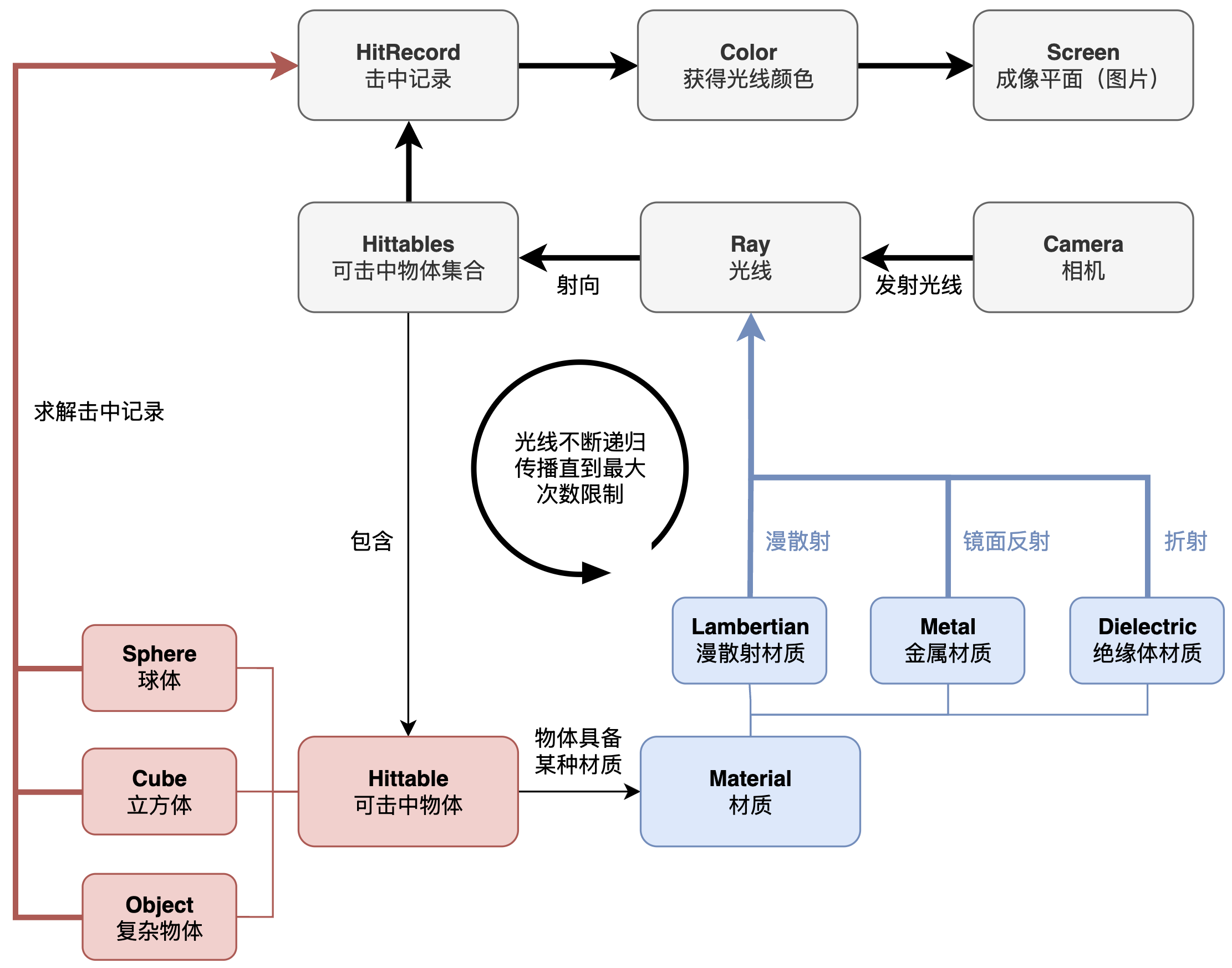
红色部分：物体部分，可击中物体 Hittable 是抽象类，可以派生各种各样的可击中物体。
蓝色部分：材质部分，物体包含材质 Material，材质是物体的固有属性，材质决定光的传播行为。
黑色部分：主流程，从相机发射光线，射向世界 Hittables，进行碰撞检测并求解击中记录，通过击中记录获得光线的颜色，然后在成像平面的对应像素上赋值。

下面是《Ray Tracing in One Weekend》最后的一个较为复杂的场景，综合了上述所说的效果。