材质

发表于 2024-10-21 分类于 Reading Disqus：本文字数： 2.9k 阅读时长 ≈ 11 分钟

慢散射材质

简单的慢散射模型

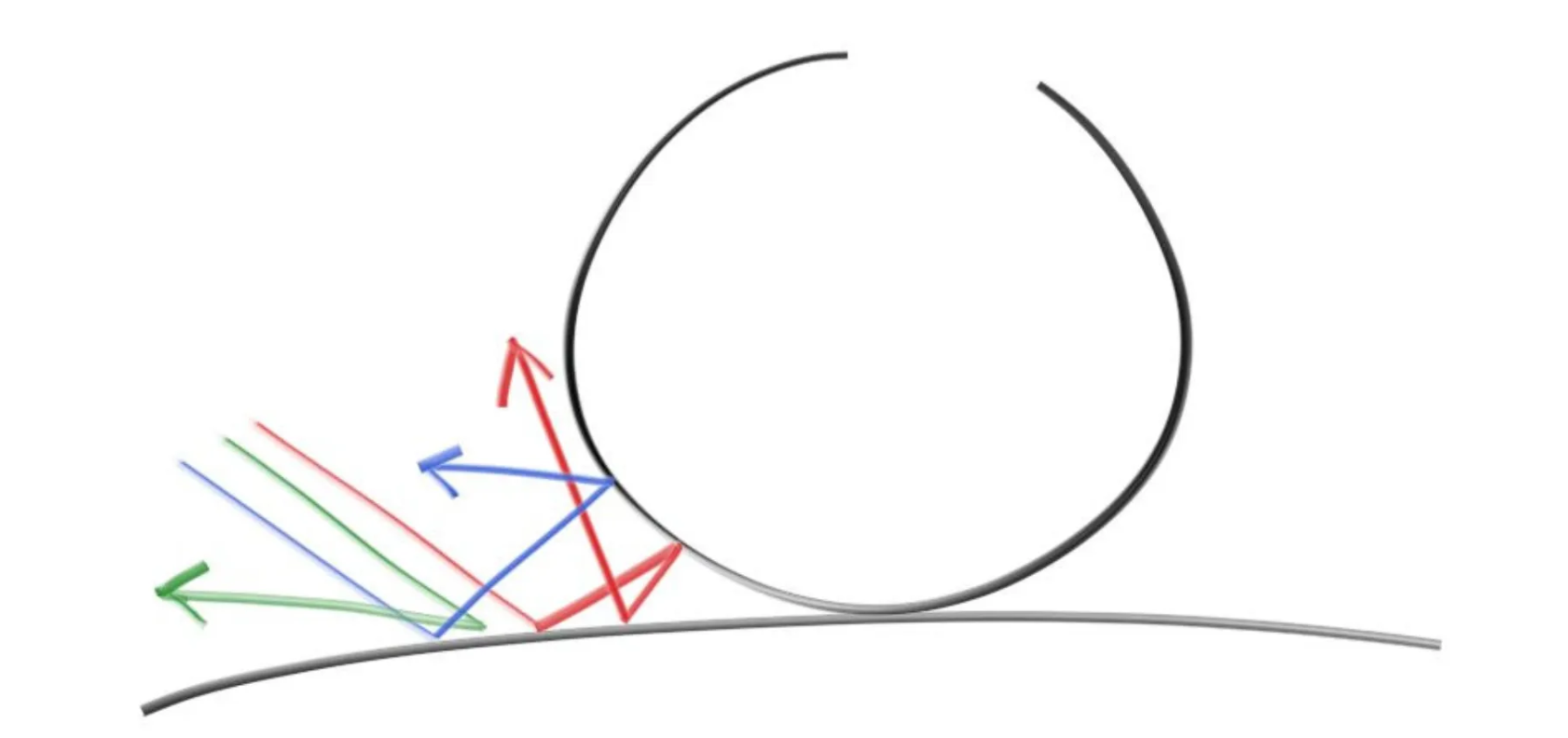
慢散射物体不会发射光，他们的颜色由自己本身的性质，以及光线散射附近物体的性质所决定。如果一条光线射向两个慢散射物体，那么这个光线会发生一些随机的反射。

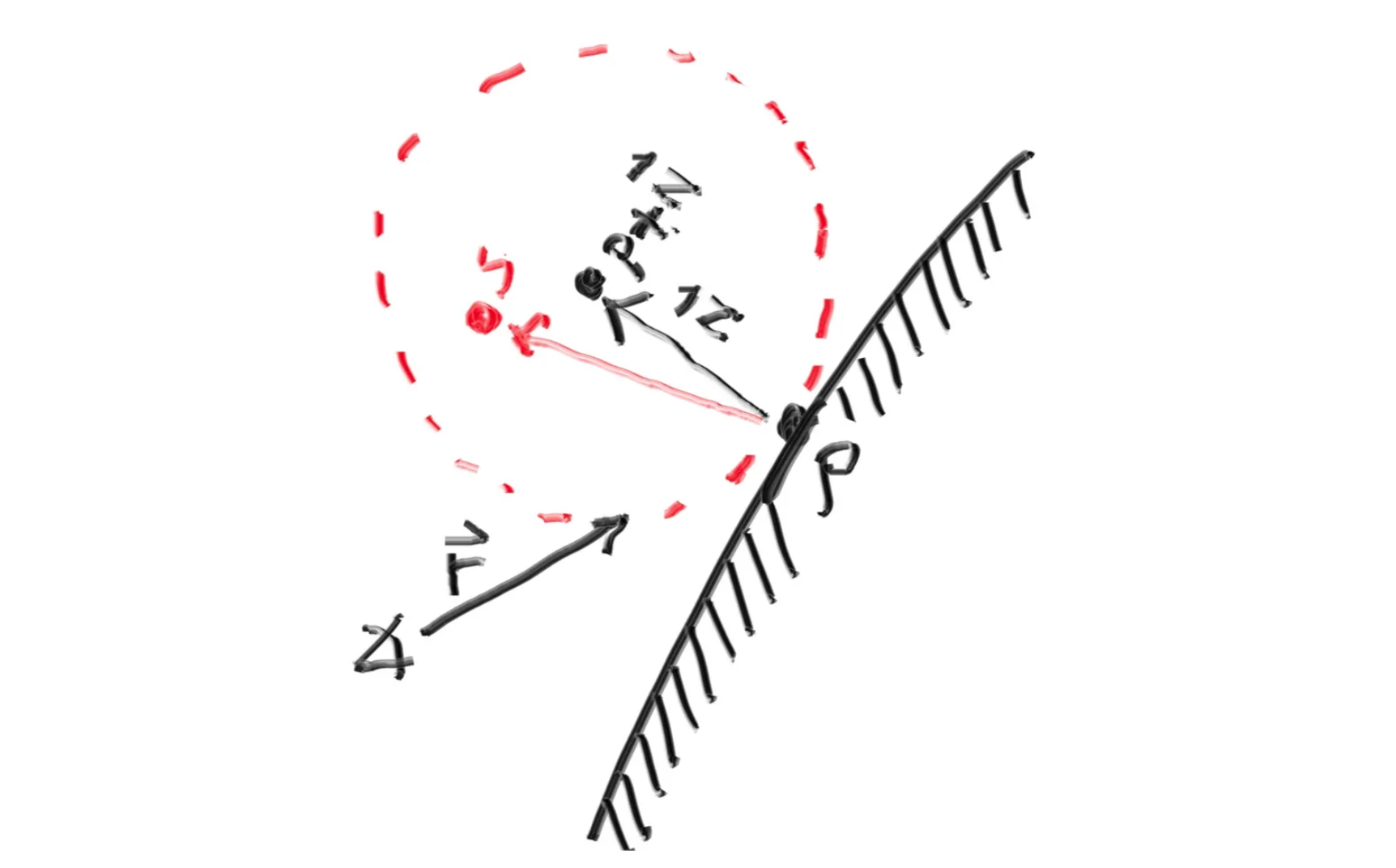
以光线与物体的接触点为切点，以该接触点的单位法向量作为半径，有一个接触点切球，在这个切球内随机取一点作为反射光线的方向。

从上图可得反射光线可以通过下面的方式计算

\[ \textbf{r}' = \textbf{r} + \textbf{p} + \textbf{N} + \textbf{s} \]

下面实现一些随机函数来随机一个单位球内的向量。最简单的方法是在立方体内随机一点，然后看这点距离原点的半径是否大于单位球，如果满足就返回，否则就继续随机。

// vec3.h
class Vec3 {
	// ...
	inline static Vec3 random(double min, double max) {
        return Vec3(randomDouble(min, max), randomDouble(min, max), randomDouble(min, max));
    }
};

Vec3 randomInUnitSphere() {
    while (true) {
        auto p = Vec3::random(-1, 1);
        if (p.lengthSquared() >= 1) continue;
        return p;
    }
}

然后在 rayColor 里使用上面的公式计算反射光线，然后再递归计算反射光线的颜色。注意到由于是递归，所以要考虑最大深度，如果超过了最大反射深度，就返回黑色（也就是没有光照）。

Color rayColor(const Ray& r, const Hittable& world, int depth) {
    // if the ray bounce limit is exceeded, no more light is gathered.
    if (depth <= 0) return Color(0, 0, 0);

    HitRecord rec;
    if (world.hit(r, 0, INFTY, rec)) {
        Point3 target = rec.p + rec.normal + randomInUnitSphere();
        return 0.5 * rayColor(Ray(rec.p, target - rec.p), world, depth - 1);
    }
    Vec3 unitDirection = unitVector(r.direction());
    auto t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

由此得到下面的结果。

Gamma 校正

可以看到上面的结果非常暗，这是因为每次反射能量都被削弱了 50%。

Color rayColor(const Ray& r, const Hittable& world, int depth) {
    // if the ray bounce limit is exceeded, no more light is gathered.
    if (depth <= 0) return Color(0, 0, 0);

    HitRecord rec;
    if (world.hit(r, 0, INFTY, rec)) {
        Point3 target = rec.p + rec.normal + randomInUnitSphere();
        return 0.5 * rayColor(Ray(rec.p, target - rec.p), world, depth - 1);
    }
    Vec3 unitDirection = unitVector(r.direction());
    auto t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

所以对于这张图片的所有颜色来说，大部分都集中在更接近 0 的区域，而一张经过 Gamma 校正的图来说，这些颜色应该遵循一定的分布，比如较为均匀地分布在 0 到 1 之间。在这个例子里，我们先采用一种简单的校正方式，也就是令 Gamma = 2。

// color.h
void writeColor(std::ostream &out, Color pixelColor, int samplesPerPixel) {
    auto r = pixelColor.x();
    auto g = pixelColor.y();
    auto b = pixelColor.z();

    auto scale = 1.0 / samplesPerPixel;
    // gamma-correct for gamma = 2.0
    r = sqrt(scale * r);
    g = sqrt(scale * g);
    b = sqrt(scale * b);

    out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
        << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
        << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}

忽略非常接近 0 的反射，得到下面的结果。

Color rayColor(const Ray& r, const Hittable& world, int depth) {
    // if the ray bounce limit is exceeded, no more light is gathered.
    if (depth <= 0) return Color(0, 0, 0);

    HitRecord rec;
    // ignore hits very close to 0.
    if (world.hit(r, 0.001, INFTY, rec)) {
        Point3 target = rec.p + rec.normal + randomInUnitSphere();
        return 0.5 * rayColor(Ray(rec.p, target - rec.p), world, depth - 1);
    }
    Vec3 unitDirection = unitVector(r.direction());
    auto t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

Lambertian 反射

在 Lambert 模型里，与上面基础模型唯一的区别是，它使用随机单位向量。

// vec3.h
Vec3 randomUnitVector() {
    return unitVector(randomInUnitSphere());
}

得到的是一个看着差不多的结果。

但可以留意到的是，影子比上面少了。这个可以理解为，因为光线的反射更为“均匀”了，这使得有更多的光线进入相机，从而使得整个画面更为光亮。

金属材质

材质的抽象类

材质需要做两件事情：

产生一条反射光线（如果有）
如果反射了，表明光的强度需要衰减多少

// material.h
class Material {

public:
    virtual bool scatter(
        const Ray& rIn, const HitRecord& rec, Color& attenuation, Ray& scattered
    ) const = 0;
};

由于光线碰到物体之后发生反射（或者被吸收）这个行为是由材质决定的，所以在击中记录 hitRecord 里应该有材质的信息。

// hittable.h
struct HitRecord {
    Point3 p;
    Vec3 normal;
    double t;
    shared_ptr<Material> material;
    bool frontFace;

    inline void setFaceNormal(const Ray& r, const Vec3& outwardNormal) {
        frontFace = dot(r.direction(), outwardNormal) < 0;
        normal = frontFace ? outwardNormal : -outwardNormal;
    }
};

物体需要有材质信息，这个材质信息会在被光线击中的时候，存放在击中记录里面。

class Sphere: public Hittable {

public:
    Point3 center;
    double radius;
    shared_ptr<Material> material;

public:
    Sphere() {}
    Sphere(Point3 c, double r): center(c), radius(r) {};

    virtual bool hit(const Ray& r, double tMin, double tMax, HitRecord& rec) const override;
    void setMaterial(shared_ptr<Material> m) {
        material = m;
    }
};

Lambertian 材质

之前的慢散射模型可以抽象到 Lambertian 材质里去，接受入射光线，通过法向量与随机向量产成反射光线，颜色衰减等，都能实现在材质的 scatter 函数里。

class Lambertian: public Material {

public:
    Color albedo;

public:
    Lambertian(const Color& a): albedo(a) {}

    virtual bool scatter(
        const Ray& rIn, const HitRecord& rec, Color& attenuation, Ray& scattered
    ) const override {
        auto scatterDirection = rec.normal + randomUnitVector();

        if (scatterDirection.nearZero()) {
            scatterDirection = rec.normal;
        }

        scattered = Ray(rec.p, scatterDirection);
        attenuation = albedo;
        return true;
    }
};

需要注意的是，如果 randomUnitVector 刚好和 normal 相反，则两者之和有可能产生一个零向量，导致一些未知问题，所以为了避免这个问题，加入 nearZero 检测，对于这种情况就直接使用 normal。

金属材质与镜面反射

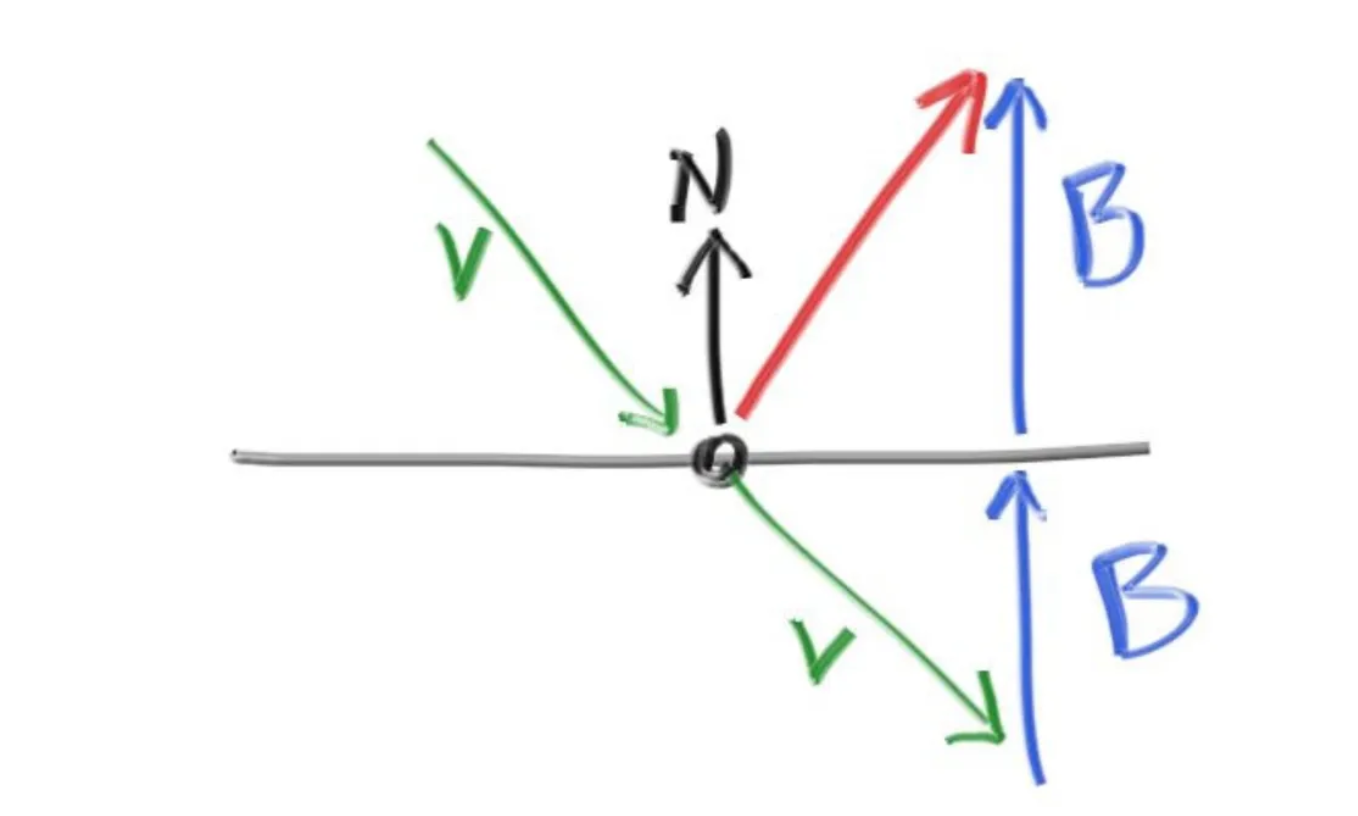
对于大多数金属来说，对入射光会进行镜面反射。

从示意图中可以看到，反射光为 \(\textbf{v} + 2\textbf{b}\)，其中法向量 \(\textbf{n}\) 为单位向量，\(\textbf{b}\) 的长度是 \(\textbf{v}\) 在法向量方向上的投影，但因为 \(\textbf{v}\) 与 \(\textbf{n}\) 反向，所以需要先反向再求点积。最后有

\[ \begin{align*} \textbf{r} &= \textbf{v} + 2\textbf{b} \\ &= \textbf{v} + 2(-\textbf{v} \cdot \textbf{n})\textbf{n} \\ &= \textbf{v} - 2 (\textbf{v} \cdot \textbf{n}) \textbf{n} \end{align*} \]

将这个反射逻辑放入金属材质里得到下面的 Metal 类。

class Metal: public Material {

public:
    Color albedo;

public:
    Metal(const Color& a): albedo(a) {}

    virtual bool scatter(
        const Ray& rIn, const HitRecord& rec, Color& attenuation, Ray& scattered
    ) const override {
        Vec3 reflected = reflect(unitVector(rIn.direction()), rec.normal);
        scattered = Ray(rec.p, reflected);
        attenuation = albedo;
        return (dot(scattered.direction(), rec.normal) > 0);
    }
};

三个球的场景

下面的场景有三个球，中间的是 Lambertian 材质，其余两个是金属材质。注意修改 rayColor 的颜色计算代码，因为目前反射光以及颜色都由材质决定了。

#include <iostream>

#include "constants.h"
#include "color.h"
#include "hittable_list.h"
#include "sphere.h"
#include "camera.h"
#include "material.h"

Color rayColor(const Ray& r, const Hittable& world, int depth) {
    // if the ray bounce limit is exceeded, no more light is gathered.
    if (depth <= 0) return Color(0, 0, 0);

    HitRecord rec;

    // ignore hits very close to 0.
    if (world.hit(r, 0.001, INFTY, rec)) {
        Ray scattered;
        Color attenuation;
        if (rec.material->scatter(r, rec, attenuation, scattered)) {
            return attenuation * rayColor(scattered, world, depth - 1);
        }
        return Color(0, 0, 0);
    }
    Vec3 unitDirection = unitVector(r.direction());
    auto t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

int main() {
    // Image
    const auto aspectRatio = 16.0 /9.0;
    const int imageWidth = 400;
    const int imageHeight = static_cast<int>(imageWidth / aspectRatio);
    const int samplesPerPixel = 100;
    const int maxDepth = 50;

    // World
    HittableList world;

    auto materialGround = make_shared<Lambertian>(Color(0.8, 0.8, 0.0));
    auto materialCenter = make_shared<Lambertian>(Color(0.7, 0.3, 0.3));
    auto materialLeft = make_shared<Metal>(Color(0.8, 0.8, 0.8));
    auto materialRight = make_shared<Metal>(Color(0.8, 0.6, 0.2));

    auto ground = make_shared<Sphere>(Point3(0, -100.5, -1), 100);
    auto center = make_shared<Sphere>(Point3(0, 0, -1), 0.5);
    auto left = make_shared<Sphere>(Point3(-1, 0, -1), 0.5);
    auto right = make_shared<Sphere>(Point3(1, 0, -1), 0.5);

    ground->setMaterial(materialGround);
    center->setMaterial(materialCenter);
    left->setMaterial(materialLeft);
    right->setMaterial(materialRight);

    world.add(ground);
    world.add(center);
    world.add(left);
    world.add(right);

    // Camera
    Camera camera;

    // Render
    std::cout << "P3\n" << imageWidth << ' ' << imageHeight << "\n255\n";

    for (int j = imageHeight - 1; j >= 0; --j) {
        std::cerr << "\r9 - Scanlines remaining: " << j << ' ' << std::flush;
        for (int i = 0; i < imageWidth; ++i) {
            Color pixelColor(0, 0, 0);
            for (int s = 0; s < samplesPerPixel; ++s) {
                auto u = (i + randomDouble()) / (imageWidth - 1);
                auto v = (j + randomDouble()) / (imageHeight - 1);
                Ray r = camera.getRay(u, v);
                pixelColor += rayColor(r, world, maxDepth);
            }
            writeColor(std::cout, pixelColor, samplesPerPixel);
        }
    }

    std::cerr << "\nDone.\n";
}

注意在初始化 world 的部分，先是创建了 4 个物体，三个球和一个“地面”，然后初始化 4 个材质，之后将材质与物体绑定，再把物体添加到世界中。下面是渲染结果。

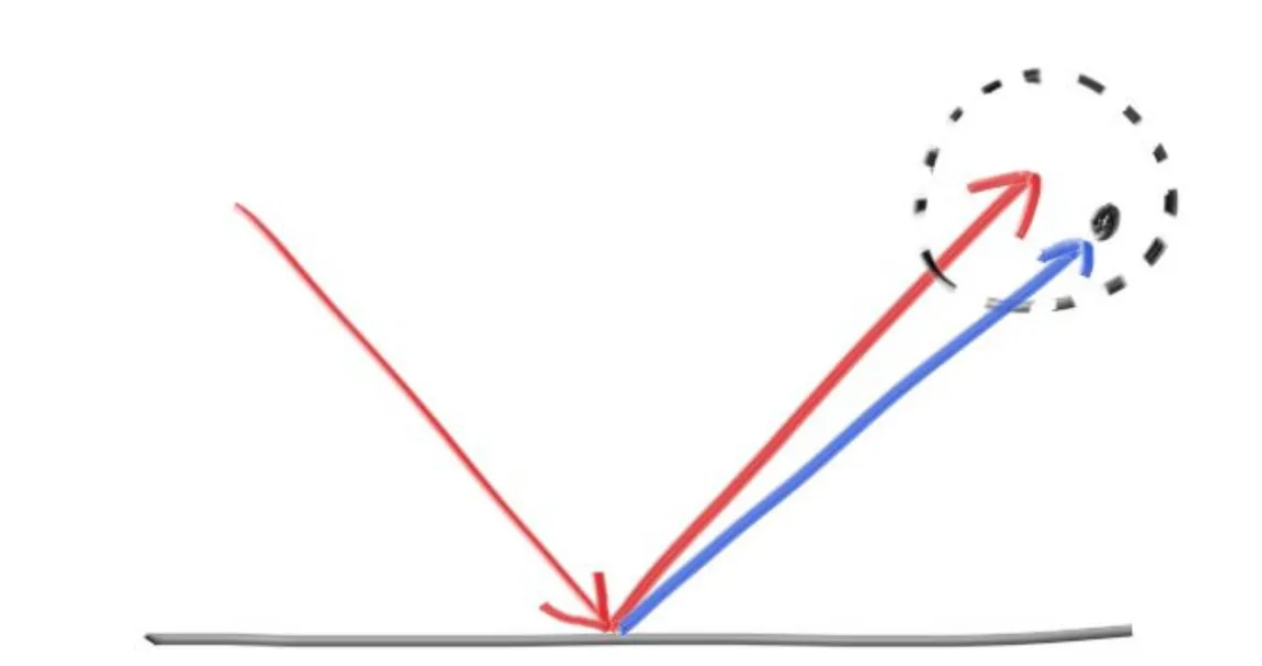
模糊反射

对于镜面反射来说，入射角等于反射角，每条光线都一样，但我们可以通过对反射光线进行一个小随机来达到模糊反射的效果。

这个对反射光线的随机球半径越大，就越模糊。

// material.h
class Metal: public Material {

public:
    Color albedo;
    double fuzz;

public:
    Metal(const Color& a, double f = 1): albedo(a), fuzz(f < 1 ? f : 1) {}

    virtual bool scatter(
        const Ray& rIn, const HitRecord& rec, Color& attenuation, Ray& scattered
    ) const override {
        Vec3 reflected = reflect(unitVector(rIn.direction()), rec.normal);
        scattered = Ray(rec.p, reflected + fuzz * randomInUnitSphere());
        attenuation = albedo;
        return (dot(scattered.direction(), rec.normal) > 0);
    }
};

给金属材质增加 fuzz 参数表明随机球的半径，然后在散射的时候加上这个随机值，得到下面的结果，可以与上面的进行对比，会发现金属球上的反射变得模糊了。

绝缘体

一些看上去透明的物体，比如水，玻璃，砖石等，都是绝缘体。当它们被光照射的时候，光线会被反射与折射。

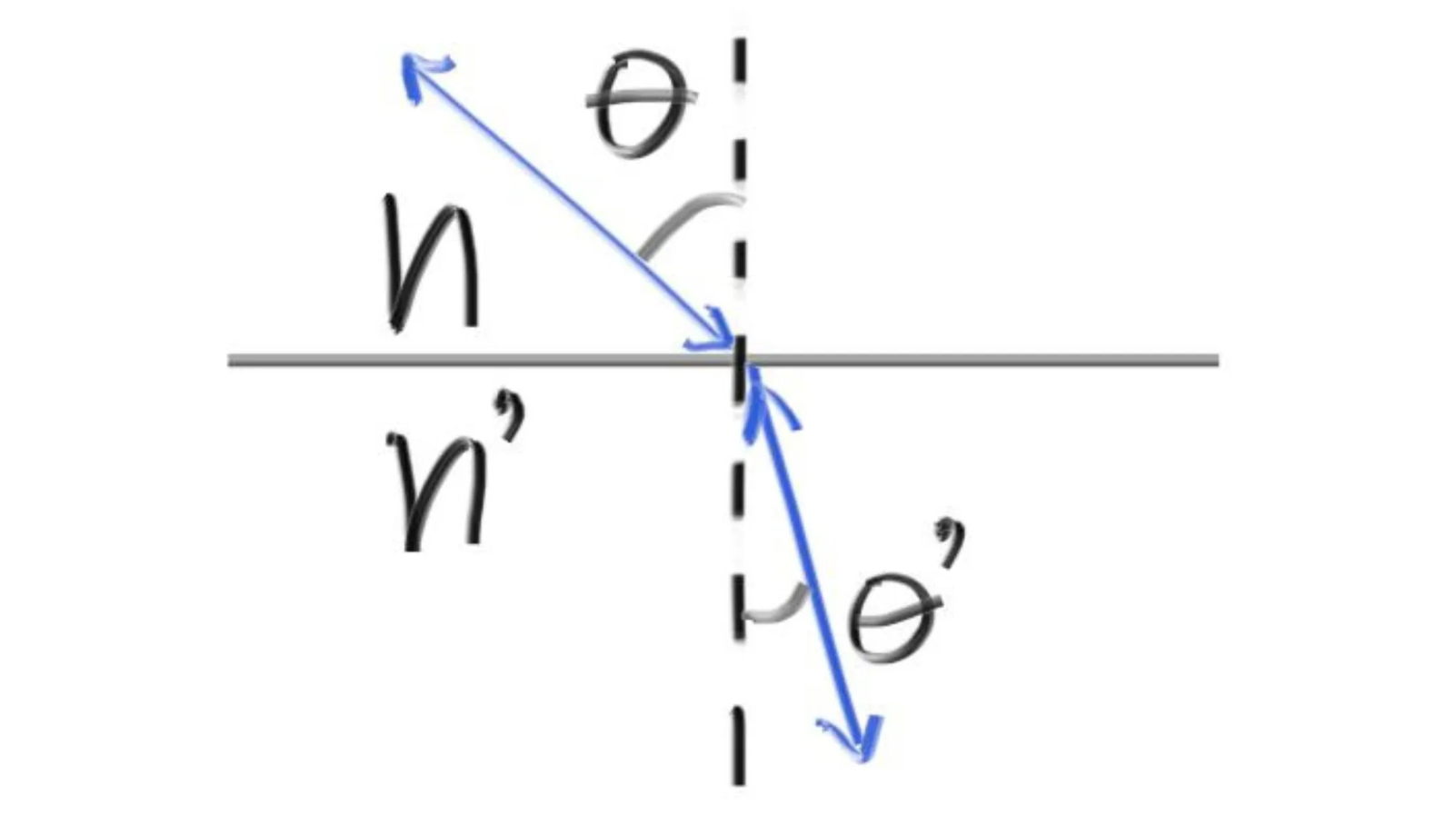
Snell 定理

Snell 定理也称为折射定理。

\[ \eta \cdot \sin \theta = \eta' \cdot \sin \theta ' \]

为了得到折射光线的方向，我们要计算 \(\theta'\)

\[ \sin \theta' = \frac{\eta}{\eta'} \cdot \sin \theta \]

在折射侧，令折射光线为 \(\textbf{R}'\)，法向量为 \(\textbf{n}'\)，它们之间的夹角为 \(\theta'\)，我们可以在法向量平衡，以及法向量垂直两个方向对 \(\textbf{R}'\) 进行分解，得到

\[ \textbf{R}' = \textbf{R}'_{\perp} + \textbf{R}'_{\shortparallel} \]

解一下方程可得

\[ \begin{align*} \textbf{R}'_{\perp} &= \frac{\eta}{\eta'}(\textbf{R} + \cos \theta \textbf{n}) \\ \textbf{R}'_\shortparallel &= -\sqrt{1 - |\textbf{R}'_\perp|^2 \textbf{n}} \end{align*} \]

上式的未知数为 \(\cos \theta\)，由余弦定理可知 \(\textbf{a} \cdot \textbf{b} = |\textbf{a}||\textbf{b}| \cos \theta\)，如果两个向量都是单位向量，那么 \(\textbf{a} \cdot \textbf{b} = \cos \theta\) 。于是可以将 \(\textbf{R}'_\perp\) 写为

\[ \textbf{R}'_\perp = \frac{\eta}{\eta'}(\textbf{R} + (-\textbf{R} \cdot \textbf{n}) \textbf{n}) \]

由此可以给向量类实现一个折射计算方法。

Vec3 refract(const Vec3& uv, const Vec3& n, double etaiOverEtat) {
    auto cosTheta = fmin(dot(-uv, n), 1.0);
    Vec3 rOutPerp = etaiOverEtat * (uv + cosTheta * n);
    Vec3 rOutParallel = -sqrt(fabs(1.0 - rOutPerp.lengthSquared())) * n;
    return rOutPerp + rOutParallel;
}

基于折射实现绝缘体材质。

class Dielectric: public Material {

public:
    double ir; // index of refraction

public:
    Dielectric(double indexOfRefraction): ir(indexOfRefraction) {}

    virtual bool scatter(
        const Ray& rIn, const HitRecord& rec, Color& attenuation, Ray& scattered
    ) const override {
        attenuation = Color(1.0, 1.0, 1.0);
        double refractionRatio = rec.frontFace ? (1.0/ir) : ir;

        Vec3 unitDirection = unitVector(rIn.direction());
        Vec3 refracted = refract(unitDirection, rec.normal, refractionRatio);

        scattered = Ray(rec.p, refracted);
        return true;
    }
};

由此可得下面的结果。

全反射

观察上面的 Snell 定理

\[ \sin \theta' = \frac{\eta}{\eta'} \cdot \sin \theta \]

如果光线从光密介质射向光疏介质，达到一定的临界角时，会产生全反射。因为 \(\sin \theta \in [0, 1]\)，如果 \(\eta / \eta' > 1\)，并且 \(\theta\) 达到一定角度使整个 \(\eta / \eta' \cdot \sin \theta > 1\)，那么就会发生反射。

if (refractionRatio * sinTheta > 1.0) {
    // Must Reflect
    ...
} else {
    // Can Refract
    ...
}

由此判断代码修改如下。

// material.h - class Dielectric
virtual bool scatter(
    const Ray& rIn, const HitRecord& rec, Color& attenuation, Ray& scattered
) const override {
    attenuation = Color(1.0, 1.0, 1.0);
    double refractionRatio = rec.frontFace ? (1.0/ir) : ir;

    Vec3 unitDirection = unitVector(rIn.direction());
    double cosTheta = fmin(dot(-unitDirection, rec.normal), 1.0);
    double sinTheta = sqrt(1.0 - cosTheta * cosTheta);

    bool cannotRefract = refractionRatio * sinTheta > 1.0;
    Vec3 direction;

    if (cannotRefract) {
        direction = reflect(unitDirection, rec.normal);
    } else {
        direction = refract(unitDirection, rec.normal, refractionRatio);
    }

    scattered = Ray(rec.p, direction);
    return true;
}

修改一下三个小球的材质，左边是 Dielectric，中间是 Lambertian，右边是 Metal。得到下面的结果。

Schlick 近似

Schlick 近似主要用于计算菲涅尔方程（Fresnel equations）中的反射和折射系数。菲涅尔方程描述了光线在介质界面上的反射和折射行为，根据入射角和介质折射率之间的关系来计算反射和折射的强度。

Schlick 近似通过使用一个简化的公式来近似计算菲涅尔方程，以提高计算效率。它基于入射角和折射率之间的关系，使用一个多项式函数来估计反射和折射的强度。

模拟一个空心玻璃球

使用负半径的话，可以使得法向量方向相反，所以在左边绝缘球体里面“内嵌”一个负半径的小球，就可以实现空心玻璃球的效果。