球，物体，法向量，抗锯齿

发表于 2024-10-13 分类于 Reading Disqus：本文字数： 2.2k 阅读时长 ≈ 8 分钟

球

位于坐标原点的球的方程为 \(x^2 + y^2 + z^2 = R^2\)，如果给定一个点在球内，则有 \(x^2 + y^2 + z^2 < R^2\)，反之则在球外。如果将球的方程写成向量形式，令 \(\textbf{P}\) 为球上一点，\(\textbf{C}\) 为圆心，则有

\[ (\textbf{P} - \textbf{C}) \cdot (\textbf{P} - \textbf{C}) = r^2 \]

满足方程的点 \(\textbf{P}\) 在球上。所以对于光线的点 \(\textbf{P}(t)\)，如果满足方程，则在球上。代入球方程并展开，有

\[ \begin{align} & (\textbf{P}(t) - \textbf{C}) \cdot (\textbf{P}(t) - \textbf{C}) = r^2 \\ & (\textbf{A} + t\textbf{b} - \textbf{C}) \cdot (\textbf{A} + t\textbf{b} - \textbf{C}) = r^2 \\ & t^2 \textbf{b} \cdot \textbf{b} + 2t \textbf{b} \cdot (\textbf{A} - \textbf{C}) + (\textbf{A} - \textbf{C})\cdot (\textbf{A} - \textbf{C}) - r^2 = 0 \end{align} \]

上面是一个简单的一元二次方程，如果无解，则光线与球没有相交，如果有一个解，则光线与球相切，如果有两个解，则光线穿过球。

根据这个判别式是否大于 0 可以简单实现光线与球相交的函数。

bool hitSphere(const Point3& center, double radius, const Ray& r) {
    Vec3 oc = r.origin() - center;
    auto a = dot(r.direction(), r.direction());
    auto b = 2.0 * dot(oc, r.direction());
    auto c = dot(oc, oc) - radius * radius;
    auto discriminant = b*b - 4*a*c;
    return (discriminant > 0);
}

如果相交则返回红色，可以得到下面的渲染结果。

Color rayColor(const Ray& r) {
    if (hitSphere(Point3(0, 0, -1), 0.5, r)) {
        return Color(1, 0, 0);
    }
    Vec3 unitDirection = unitVector(r.direction());
    auto t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

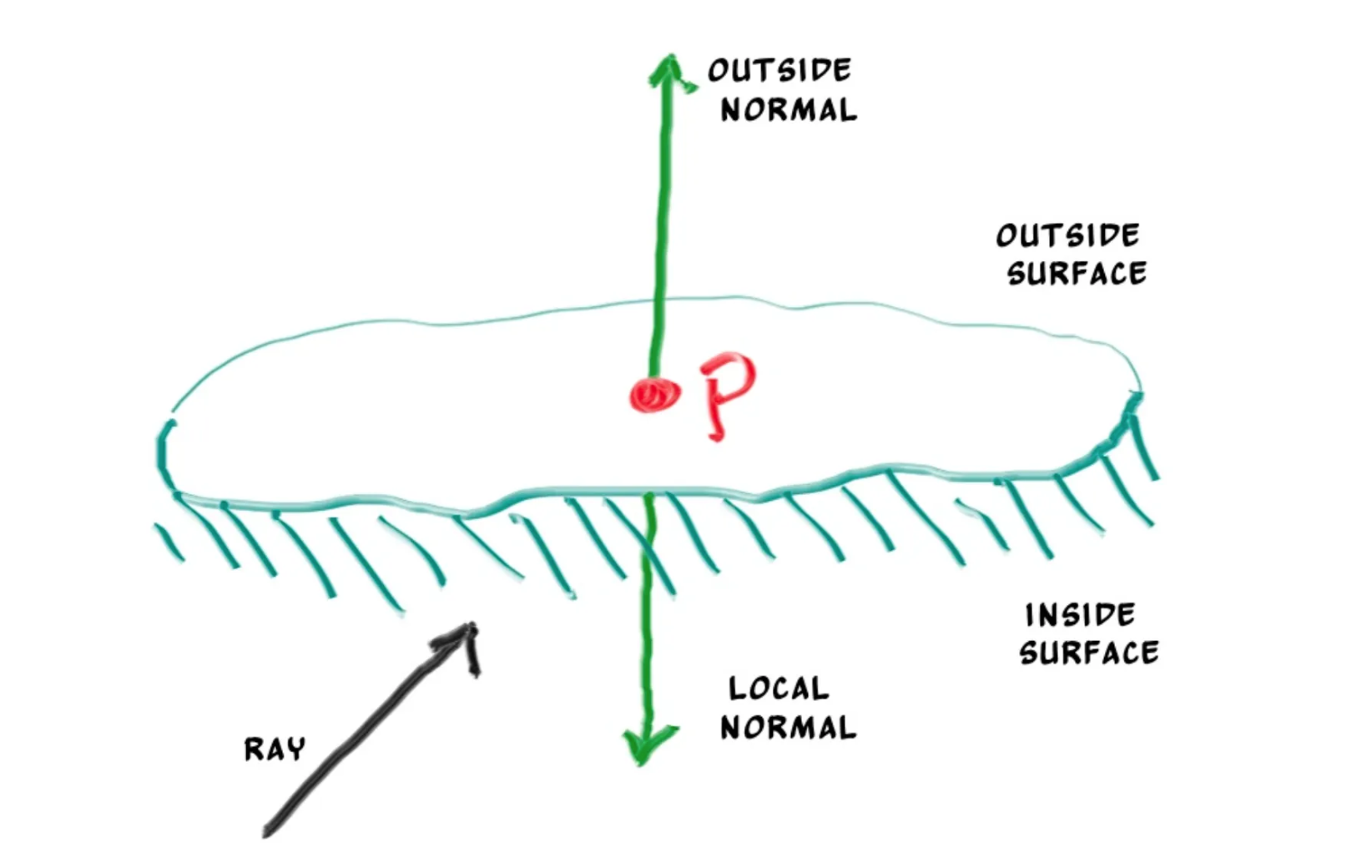
法向量

每个物体有光影的变化，是因为光照射到物体的时候会有不同方向的反射，而法向量是一个垂直于物体表面的向量，可以通过这个法向量与光线的夹角来表现出这种光影。

一般习惯是会让这些面法向量为单位向量。

double hitSphere(const Point3& center, double radius, const Ray& r) {
    Vec3 oc = r.origin() - center;
    auto a = dot(r.direction(), r.direction());
    auto b = 2.0 * dot(oc, r.direction());
    auto c = dot(oc, oc) - radius * radius;
    auto discriminant = b*b - 4*a*c;

    if (discriminant < 0) {
        return -1.0;
    } else {
        return (-b - sqrt(discriminant)) / (2.0*a);
    }
}

Color rayColor(const Ray& r) {
    auto t = hitSphere(Point3(0, 0, -1), 0.5, r);
    if (t > 0.0) {
        Vec3 N = unitVector(r.at(t) - Vec3(0, 0, -1));
        return 0.5*Color(N.x() + 1, N.y() + 1, N.z() + 1);
    }
    Vec3 unitDirection = unitVector(r.direction());
    t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

上面的代码将光线与球的交点直接计算出来，如果判别式大于 0，则用求根公式直接计算出 t，然后用 t 计算交点，用交点与圆心的向量作为法向量，然后先简单用法向量作为颜色（因为目前没有光源）。由此得到下面的结果。

物体

对可击中物体的抽象

世界中的物体其实都可以被光线“击中”，可以对这些可击中物体进行抽象，这样后面光线追踪的目标就是这些可击中物体，对这个抽象类进行派生，得到各种各样不同的物体，比如球体，立方体，甚至复杂模型等。

下面是对简单可击中物体的定义。

// hittable.h
#ifndef HITTABLE_H
#define HITTABLE_H

#include "ray.h"

struct HitRecord {
    point3 p;
    vec3 normal;
    double t;
};

class Hittable {

public:
    virtual bool hit(const Ray& r, double tMin, double tMax, HitRecord& rec) const = 0;
};

#endif

有了可击中物体这个基类，就可以继承从而得到其他形状。下面是对球体的定义。

// sphere.h
#ifndef SPHERE_H
#define SPHERE_H

#include "hittable.h"

class Sphere: public Hittable {

public:
    Point3 center;
    double radius;
public:
    Sphere() {}
    Sphere(Point3 c, double r): center(c), radius(r) {};

    virtual bool hit(const Ray& r, double tMin, double tMax, HitRecord& rec) const override;
};

bool Sphere::hit(const Ray& r, double tMin, double tMax, HitRecord& rec) const {
    Vec3 oc = r.origin() - center;
    auto a = r.direction.lengthSquared();
    auto halfB = dot(oc, r.direction());
    auto c = oc.lengthSquared() - radius * radius;
    auto discriminant = halfB*halfB - a*c;

    if (discriminant < 0) return false;

    auto sqrtd = sqrt(discriminant);

    // find the nearest root that lies in the acceptable rage.
    auto root = (-halfB - sqrtd) / a;
    if (root < tMin || tMax < root) {
        root = (-halfB + sqrtd) / a;
        if (root < tMin || tMax < root) return false;
    }

    rec.t = root;
    rec.p = r.at(rec.t);
    rec.normal = (rec.p - center) / radius;

    return true;
}

#endif

面的方向

使用面法向量与光线的点积，可以方便地判断方向。如果点积大于 0，那两个向量的夹角就是锐角，也就是两个向量“同向”。

在这个教程里，永远希望法向量朝向光线的入射方向，也就是，如果光源在物体外部，那么物体的面法向量向着外部，如果光源在物体内部，那么物体的法向量向着内部。

bool frontFace;
if (dot(rayDirection, outwardNormal) > 0.0) {
	// ray is inside the sphere
	normal = -outwardNormal;
	frontFace = false;
} else {
	// ray is outside the sphere
	normal = outwardNormal;
	frontFace = true;
}

我们把这些记录在 HitRecord 里。

struct HitRecord {
    point3 p;
    vec3 normal;
    double t;
    bool frontFace;

    inline void setFaceNormal(const Ray& r, const Vec3& outwardNormal) {
        frontFace = dot(r.direction(), outwardNormal) < 0;
        normal = frontFace ? outwardNormal : -outwardNormal;
    }
};

可击中物体集合

在可击中物体之上再进行一层抽象，将可击中物体的集合看成一整个可击中物体，光线发出之后，对集合里的每个物体进行检查，找出最近的可击中物体。

#ifndef HITTABLE_LIST_H
#define HITTABLE_LIST_H

#include "hittable.h"

#include <memory>
#include <vector>

using std::shared_ptr;
using std::make_shared;

class HittableList: public Hittable {

public:
    std::vector<shared_ptr<Hittable>> objects;
public:
    HittableList() {}
    HittableList(shared_ptr<Hittable> object) { add(object); }

    void clear() { objects.clear(); }
    void add(shared_ptr<Hittable> object) { objects.push_back(object); }

    virtual bool hit(const Ray& r, double tMin, double tMax, HitRecord& rec) const override;
}

bool HittableList::hit(const Ray& r, double tMin, double tMax, HitRecord& rec) const {
    HitRecord tempRec;
    bool hitAnything = false;
    auto closestSoFar = tMax;

    // search for the closest hittable object.
    // gradually shrinks the tMax.
    for (const auto& object: objects) {
        if (object->hit(r, tMin, closestSoFar, tempRec)) {
            hitAnything = true;
            closestSoFar = tempRec.t;
            rec = tempRec;
        }
    }

    return hitAnything;
}

#endif

在主函数中使用 HittableList 定义一个 world，里面包含两个球体。

#include <iostream>

#include "constants.h"
#include "color.h"
#include "hittable_list.h"
#include "sphere.h"

Color rayColor(const Ray& r, const Hittable& world) {
    HitRecord rec;
    if (world.hit(r, 0, INFTY, rec)) {
        return 0.5 * (rec.normal + Color(1, 1, 1));
    }
    Vec3 unitDirection = unitVector(r.direction());
    auto t = 0.5 * (unitDirection.y() + 1.0);
    return (1.0-t) * Color(1.0, 1.0, 1.0) + t*Color(0.5, 0.7, 1.0);
}

int main() {
    // Image
    const auto aspectRatio = 16.0 /9.0;
    const int imageWidth = 400;
    const int imageHeight = static_cast<int>(imageWidth / aspectRatio);

    // World
    HittableList world;
    world.add(make_shared<Sphere>(Point3(0, 0, -1), 0.5));
    world.add(make_shared<Sphere>(Point3(0, -100.5, -1), 100));

    // Camera
    auto viewportHeight = 2.0;
    auto viewportWidth = aspectRatio * viewportHeight;
    auto focalLength = 1.0;

    auto origin = Point3(0, 0, 0);
    auto horizontal = Vec3(viewportWidth, 0, 0);
    auto vertical = Vec3(0, viewportHeight, 0);
    auto lowerLeftCorner = origin - horizontal/2 - vertical/2 - Vec3(0, 0, focalLength);

    // Render
    std::cout << "P3\n" << imageWidth << ' ' << imageHeight << "\n255\n";

    for (int j = imageHeight - 1; j >= 0; --j) {
        std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
        for (int i = 0; i < imageWidth; ++i) {
            auto u = double(i) / (imageWidth - 1);
            auto v = double(j) / (imageHeight - 1);
            Ray r(origin, lowerLeftCorner + u*horizontal + v*vertical - origin);
            Color pixelColor = rayColor(r, world);
            writeColor(std::cout, pixelColor);
        }
    }

    std::cerr << "\nDone.\n";
}

由此得到下面的渲染结果。

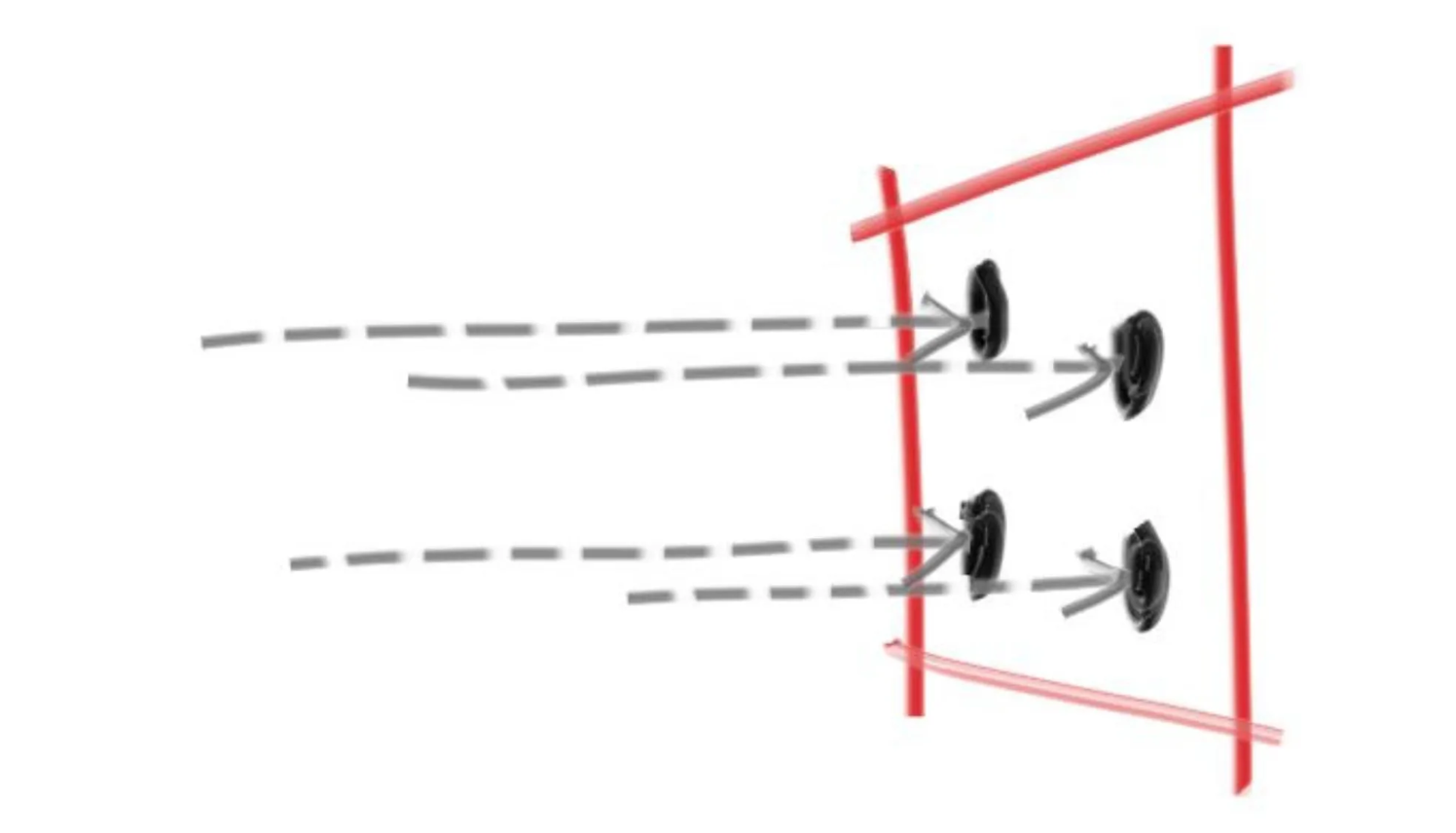
抗锯齿

通常用照相机拍照的时候，不会有非常明显的锯齿现象，因为边缘附近的像素会混合一些前景色和背景色，这个问题可以通过对一些像素取均值来解决。

随机函数

下面定义两个基础随机函数，用于返回不同区间的实数。

inline double randomDouble() {
    // returns a random real in [0, 1)
    return rand() / (RAND_MAX + 1.0);
}

inline double randomDouble(double min, double max) {
    // returns a random real in [min, max)
    return min + (max - min) * randomDouble();
}

采样

对于某个像素点来说，如果有多个光线击中这个像素点，那么这个像素的颜色就是多个光线颜色的均值。

通过将相机进行抽象，我们可以把这个采样的逻辑放在相机里。

// camera.h
#ifndef CAMERA_H
#define CAMERA_H

#include "constants.h"

class Camera {

public:
    Point3 origin;
    Point3 lowerLeftCorner;
    Vec3 horizontal;
    Vec3 vertical;

public:
    Camera() {
        // Image
        const auto aspectRatio = 16.0 /9.0;
        auto viewportHeight = 2.0;
        auto viewportWidth = aspectRatio * viewportHeight;
        auto focalLength = 1.0;

        origin = Point3(0, 0, 0);
        horizontal = Vec3(viewportWidth, 0, 0);
        vertical = Vec3(0, viewportHeight, 0);
        lowerLeftCorner = origin - horizontal/2 - vertical/2 - Vec3(0, 0, focalLength);
    }

    Ray getRay(double u, double v) const {
        return Ray(origin, lowerLeftCorner + u*horizontal + v*vertical - origin);
    }
};

#endif

之后增加一个截取函数，用于将一个输入数字截取到指定范围内。

// constants.h
inline double clamp(double x, double min, double max) {
    if (x < min) return min;
    if (x > max) return max;
    return x;
}

然后我们写一个求采样均值的颜色函数，接受采样数量，然后将颜色求均值。

// color.h
void writeColor(std::ostream &out, Color pixelColor, int samplesPerPixel) {
    auto r = pixelColor.x();
    auto g = pixelColor.y();
    auto b = pixelColor.z();

    auto scale = 1.0 / samplesPerPixel;
    r *= scale;
    g *= scale;
    b *= scale;

    out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
        << static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
        << static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}

最后我们在主函数里，之前是一个像素对应一条光线，目前我们改成每个像素对应多条光线，而光线的起点则通过随机值生成，最后再使用改进后的颜色函数来求均值。

int main() {
    // Image
    const auto aspectRatio = 16.0 /9.0;
    const int imageWidth = 400;
    const int imageHeight = static_cast<int>(imageWidth / aspectRatio);
    const int samplesPerPixel = 100;

    // World
    HittableList world;
    world.add(make_shared<Sphere>(Point3(0, 0, -1), 0.5));
    world.add(make_shared<Sphere>(Point3(0, -100.5, -1), 100));

    // Camera
    Camera camera;

    // Render
    std::cout << "P3\n" << imageWidth << ' ' << imageHeight << "\n255\n";

    for (int j = imageHeight - 1; j >= 0; --j) {
        std::cerr << "\r6 - Scanlines remaining: " << j << ' ' << std::flush;
        for (int i = 0; i < imageWidth; ++i) {
            Color pixelColor(0, 0, 0);
            for (int s = 0; s < samplesPerPixel; ++s) {
                auto u = (i + randomDouble()) / (imageWidth - 1);
                auto v = (j + randomDouble()) / (imageHeight - 1);
                Ray r = camera.getRay(u, v);
                pixelColor += rayColor(r, world);
            }
            writeColor(std::cout, pixelColor, samplesPerPixel);
        }
    }

    std::cerr << "\nDone.\n";
}

下面是抗锯齿前后的对比。