word2vec
基于推理的方法和神经网络
基于计数方法的问题
基于计数的方法根据一个单词周围的单词的出现频数来表示该单词。具体来说,先生成所有单词的共现矩阵,在对这个矩阵进行 SVD,已获得密集向量。但是,基于计数的方法在处理大规模语料库的时候会出现问题。
对于一个 \(n \times n\) 的矩阵,SVD 的复杂度为 \(O(n^3)\)。
而基于推理的方法使用神经网络,通常在 mini-batch 数据上进行学习,这意味着神经网络一次只需要看一部分学习数据,并反复更新权重。
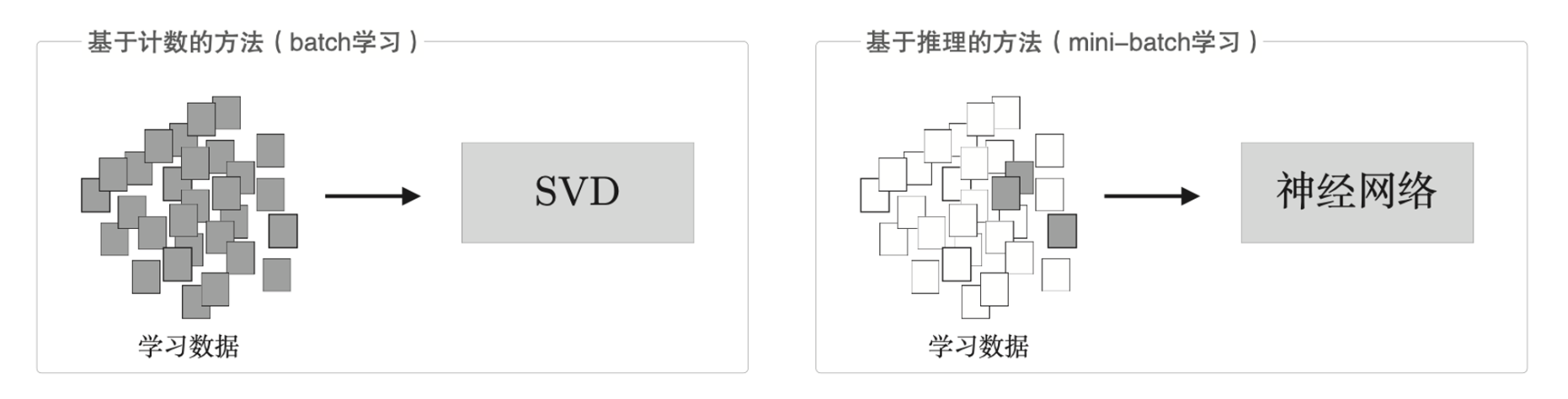
一次性处理全部数据与批量处理小部分数据的区别。
基于推理的方法的概要
基于推理的方法的主要操作是“推理”。

基于两边的单词(上下文),预测“?”处出现什么单词
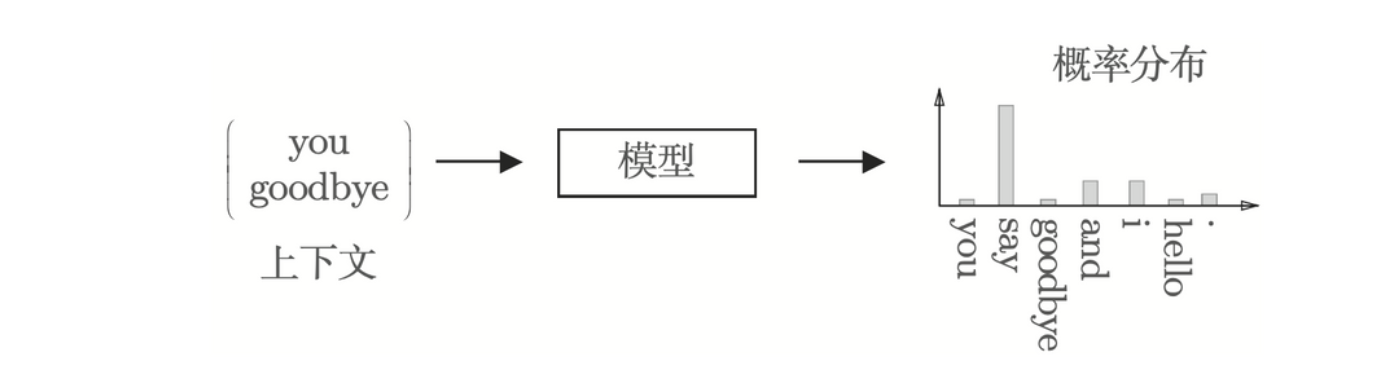
基于推理的方法:输入上下文,模型输出各个单词的出现概率
神经网络中单词的处理方法
要用神经网络来处理单词,就需要将单词转化为 one-hot 的表示。

单词、单词 ID 以及它们的 one-hot 表示
简单的 word2vec
原版的 word2vec 提出了名为 continuous bag-of-words(CBOW)的模型作为神经网络。
CBOW 模型的推理
CBOW 的输入是上下文,假设上下文用 ['you', 'goodbye']
两个单词,将其转换为 one-hot 表示,如果有 \(N\) 个单词,则输入层有 \(N\) 个。
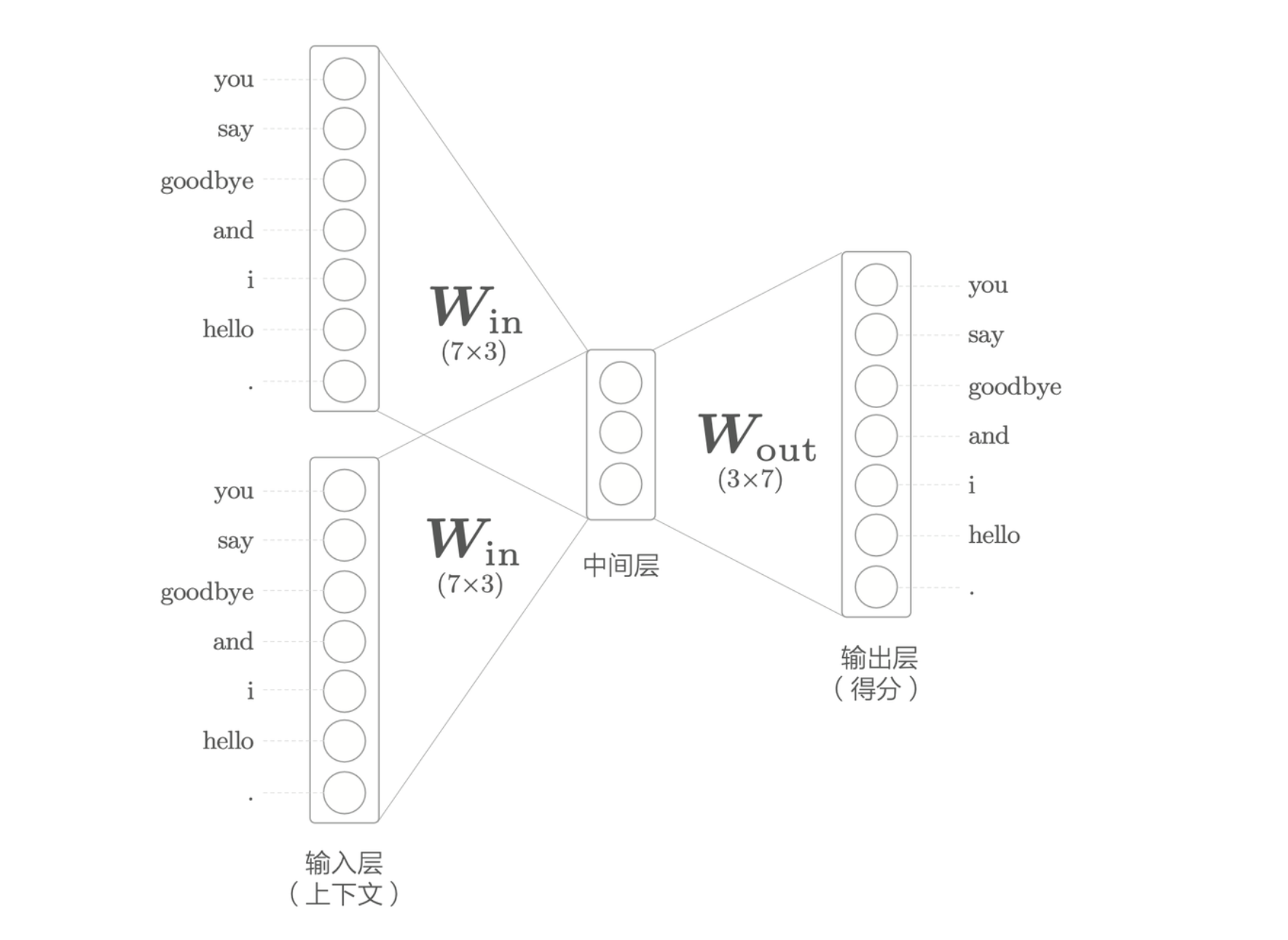
CBOW 模型的网络结构
其中,中间层是输入层各个层做完变换之后得到的平均值。输出层是各个单词的得分,它的值越大,则说明对应单词的出现概率就越高。
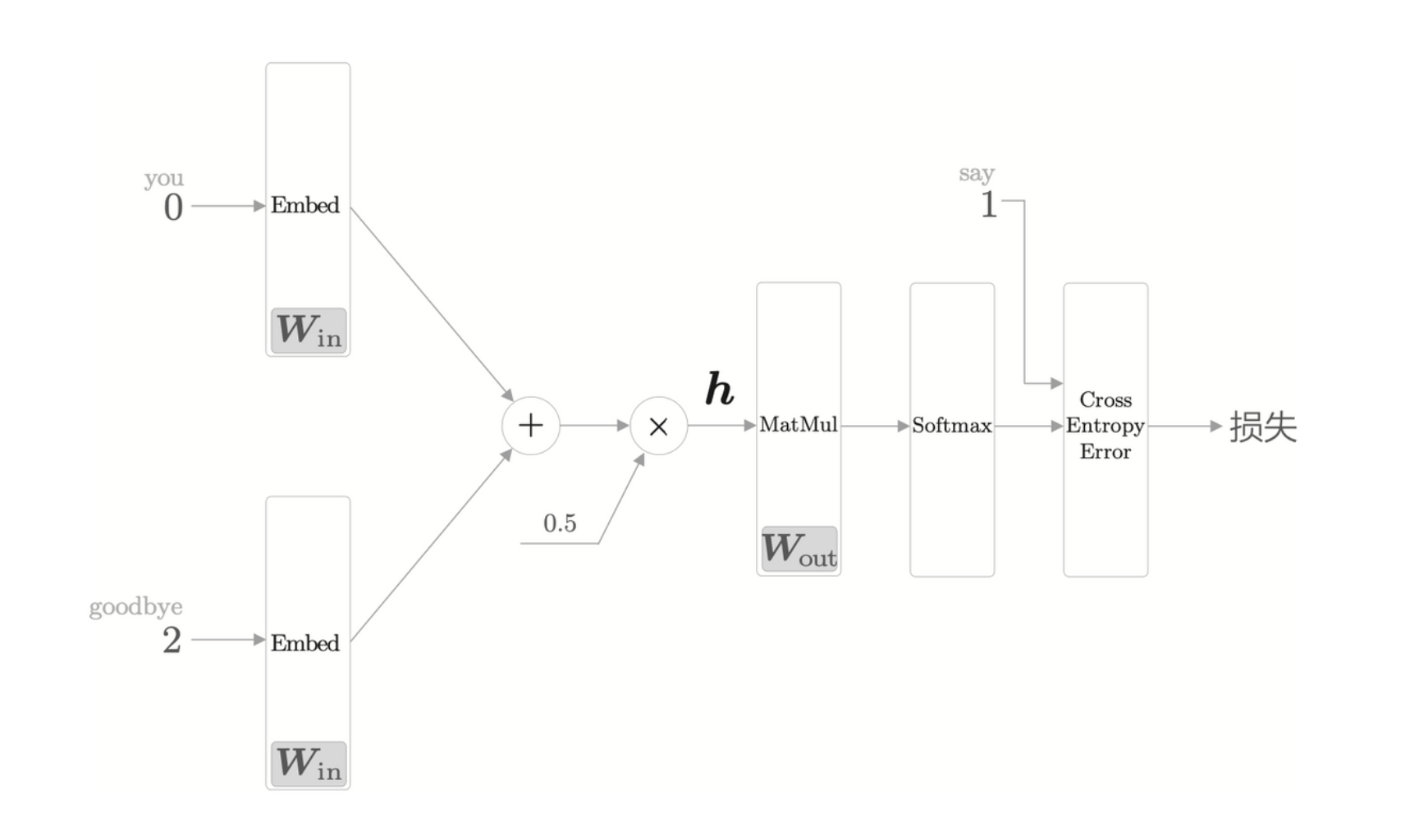
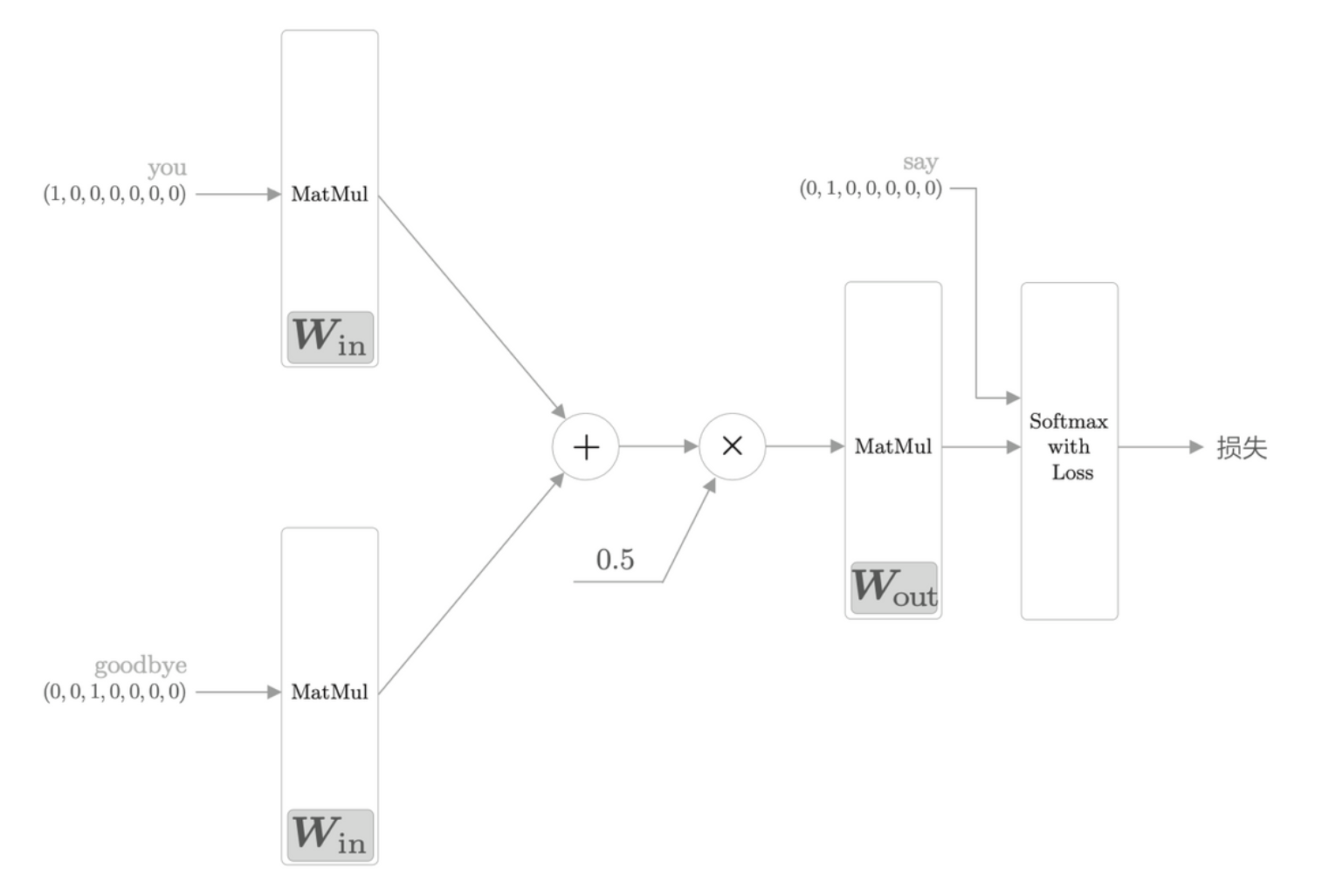
CBOW 模型的学习
其实就是使用了交叉熵误差来计算误差,然后反向传播进行学习。
word2vec 的权重和分布式表示
如前所述,word2vec 中使用的网络有两个权重,分别是输入侧的全连接层权重和输出侧的全连接层权重。一般而言,输入侧的权重 \(\textbf{W}_{in}\) 的每一行对应于各个单词的分布式表示。输出侧的权重 \(\textbf{W}_{out}\) 也同样保存了对单词含义进行编码的向量。就 word2vec 而言,倾向于只使用 \(\textbf{W}_{in}\) 作为最终的单词的分布式表示。
学习数据的准备
上下文和目标词
word2vec 中使用的神经网络的输入是上下文,它的正确解标签是被这些上下文包围在中间的单词,即目标词。
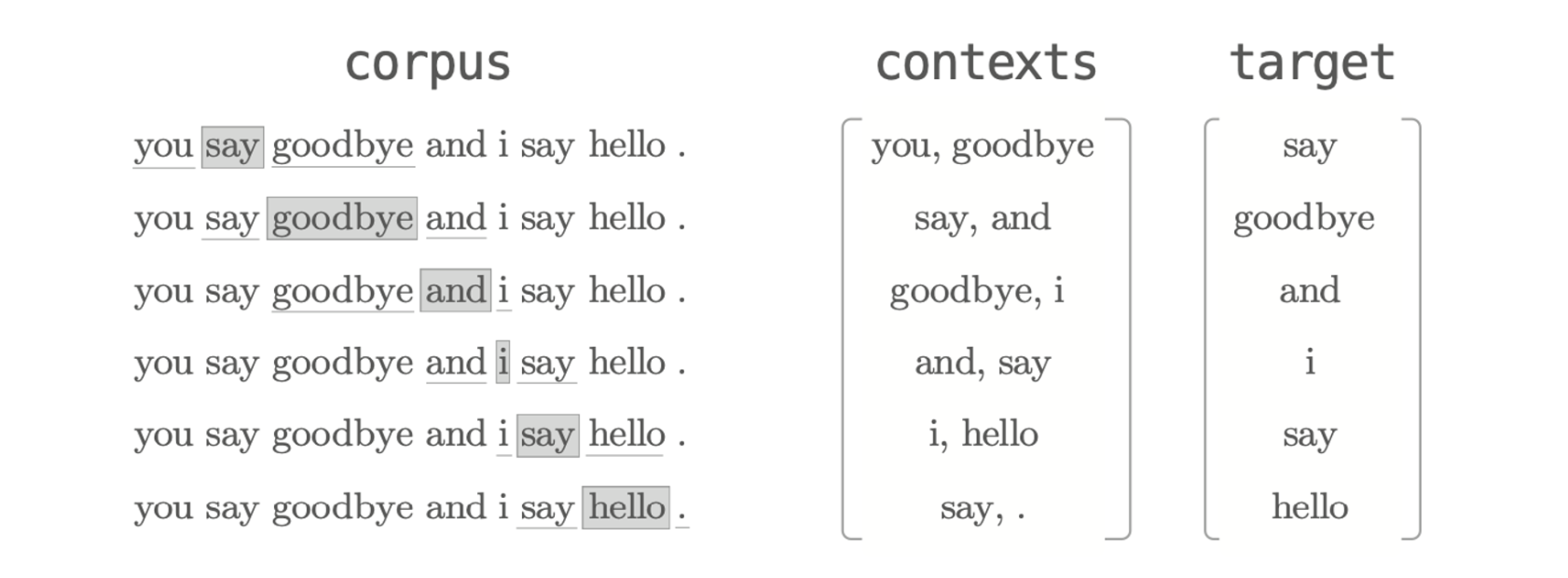
从语料库生成上下文和目标词
转化为 one-hot 表示

CBOW 模型的实现
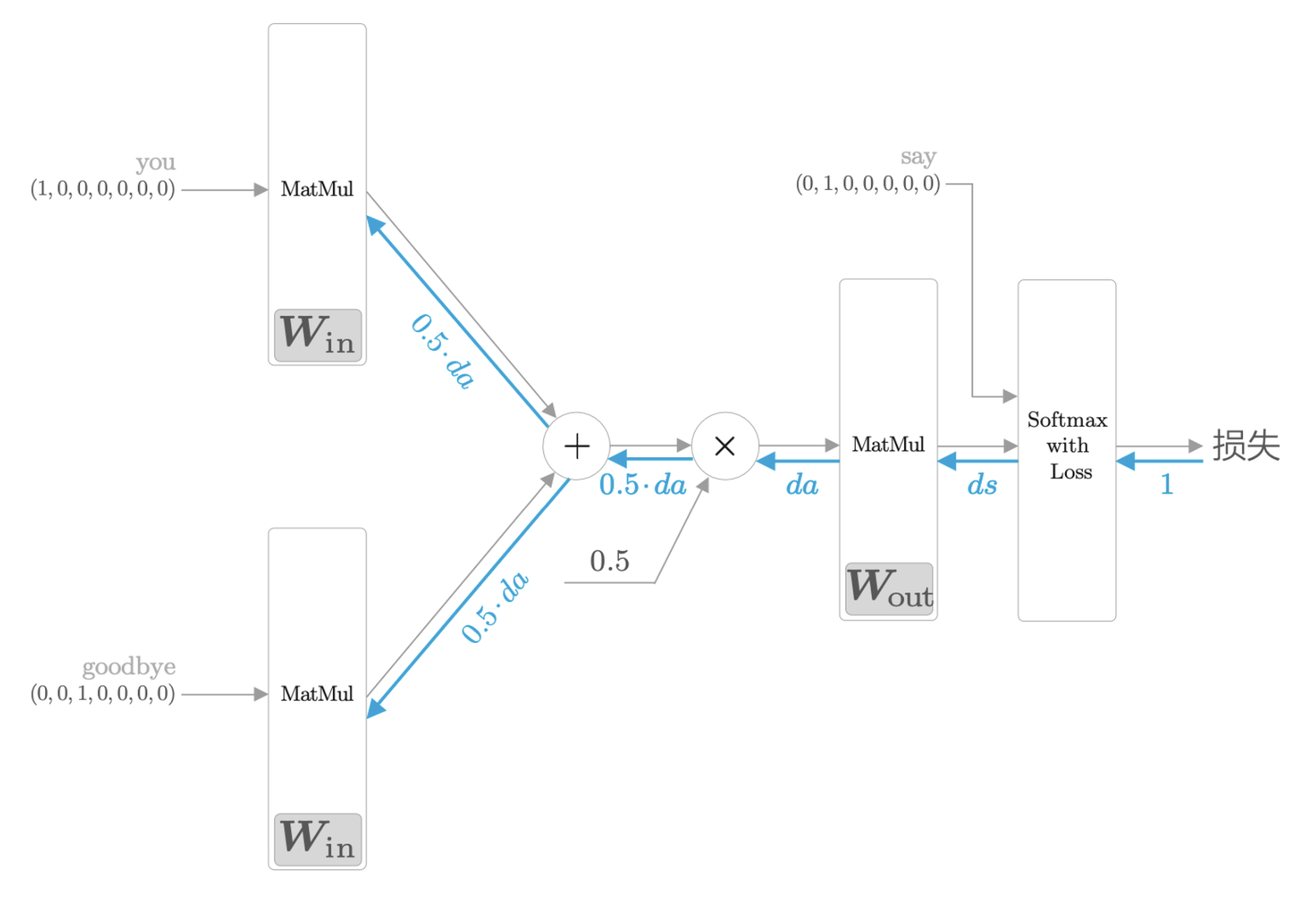
CBOW 模型和概率
考虑包含单词 \(w_1, w_2,\dots w_T\) 的语料库,考虑窗口大小为 1。当给定上下文 \(w_{t - 1}\) 和 \(w_{t+1}\) 的时候,目标词 \(w_t\) 的后验概率为
\[ P(w_t | w_{t - 1}, w_{t + 1}) \]
交叉熵误差函数是 \(L = -\sum_k t_k \log y_k\),类似的,CBOW 的损失函数为
\[ L = -\log P(w_t | w_{t - 1}, w_{t + 1}) \]
这也称为负对数似然(negative log likelihood)。上面只是其中一笔样本数据的损失函数,扩展到整个语料库,损失函数为
\[ L = -\frac{1}{T} \sum_{t = 1}^T \log P(w_t | w_{t - 1}, w_{t + 1}) \]
skip-gram 模型
skip-gram 模型是翻转了 CBOW 型处理上下文和目标词的模型。

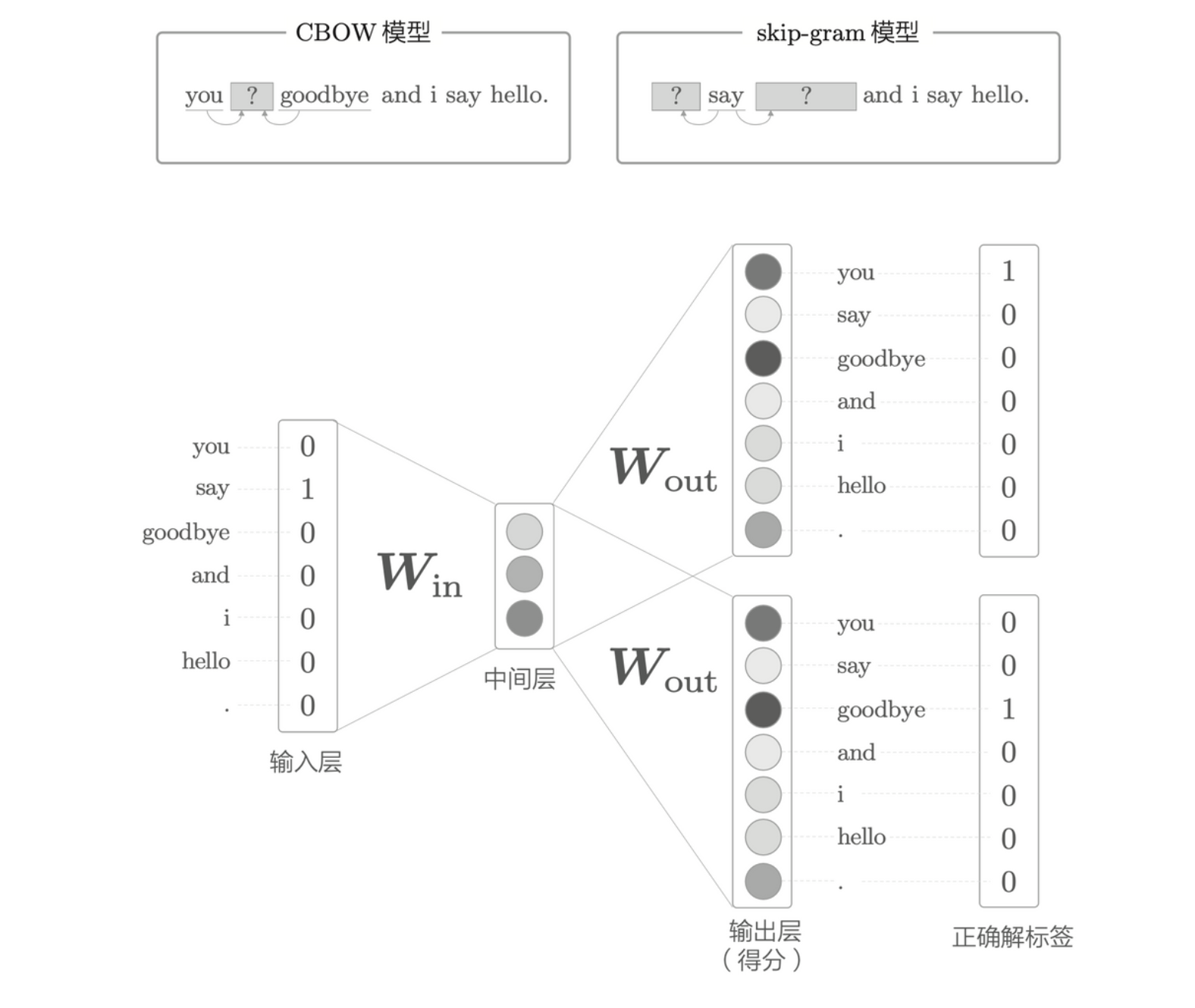
skip-gram 模型的例子
类似地,对于 skip-gram 来说,使用 \(w_t\) 来预测上下文 \(w_{t - 1}\) 和 \(w_{t + 1}\),其后验概率为
\[ P(w_{t - 1}, w_{t + 1}| w_t) \]
skip-gram 的一个假设是,上下文的单词之间没有相关性。故上式可以分解为
\[ P(w_{t - 1}, w_{t + 1}| w_t) = P(w_{t - 1}| w_t)P(w_{t + 1}| w_t) \]
代入交叉熵误差函数,可以得到 skip-gram 的损失函数
\[ \begin{align*} L &= -\log P(w_{t - 1}, w_{t + 1}| w_t) \\ &= -\log P(w_{t - 1}| w_t)P(w_{t + 1}| w_t) \\ &= -[\log P(w_{t - 1}| w_t) + \log P(w_{t + 1}| w_t)] \end{align*} \]
扩展到整个语料库,可以得到
\[ L = -\frac{1}{T} \sum_{t = 1}^T [\log P(w_{t - 1}| w_t) + \log P(w_{t + 1}| w_t)] \]
高速化
当词汇量数量非常庞大,比如 100 万个,而神经元有 100 个的时候, word2vec 的处理过程如下
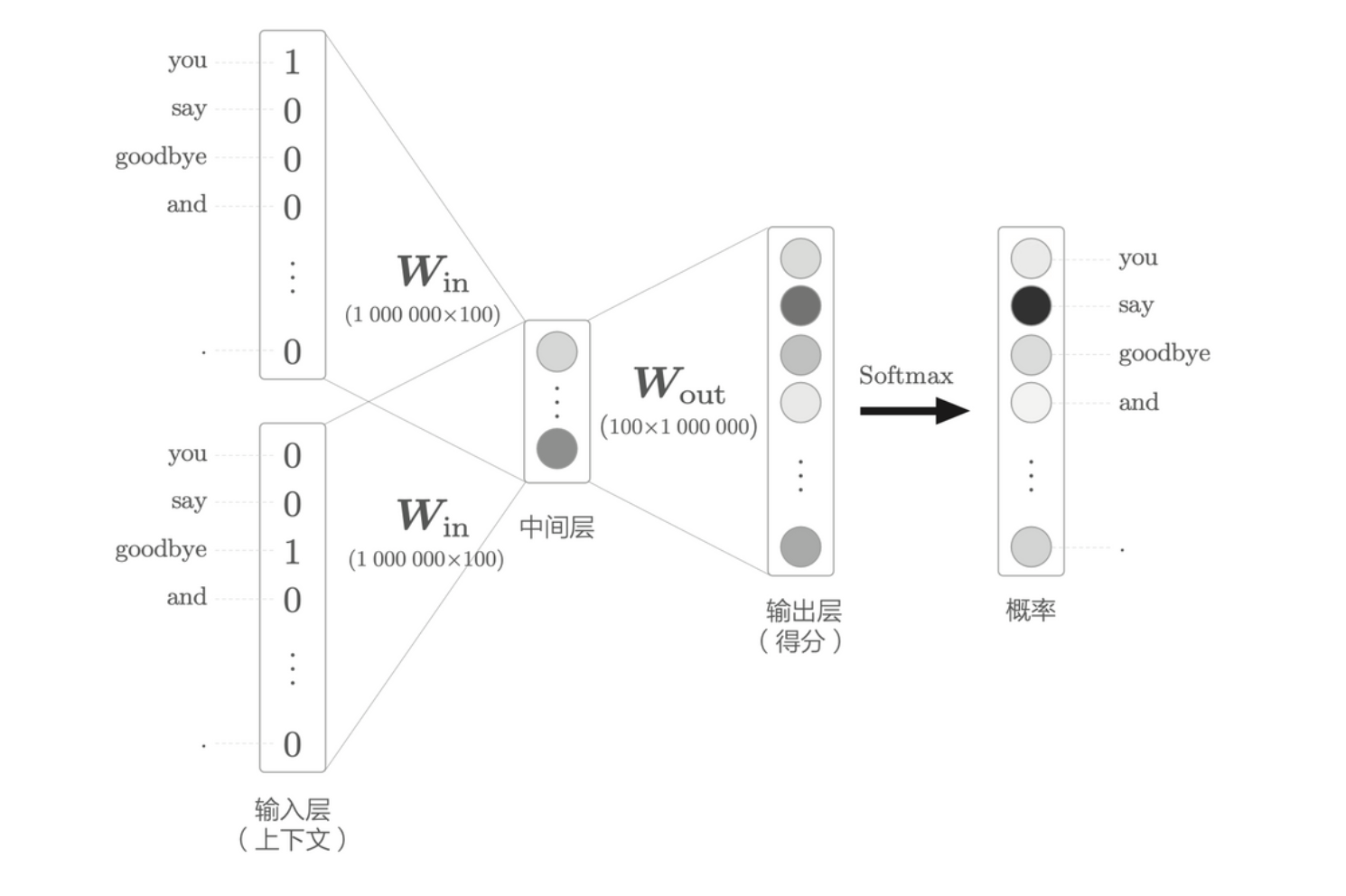
计算瓶颈会出现在
- 输入层的 one-hot 表示和权重矩阵 \(\textbf{W}_{in}\) 的乘积
- 中间层和权重矩阵 \(\textbf{W}_{out}\) 的乘积以及 Softmax 层的计算。
Embedding 层
由于单词转化为 one-hot 表示,并且输入了 MatMul 层,在计算乘积的时候,实际上只是从 \(\textbf{W}_{in}\) 里提取出了 one-hot 对应的那一行权重而已,所以这个不需要真的进行矩阵乘积,而只需要创建一个从权重参数中抽取“单词 ID 对应行”的层即可,这里成为 Embedding 层。
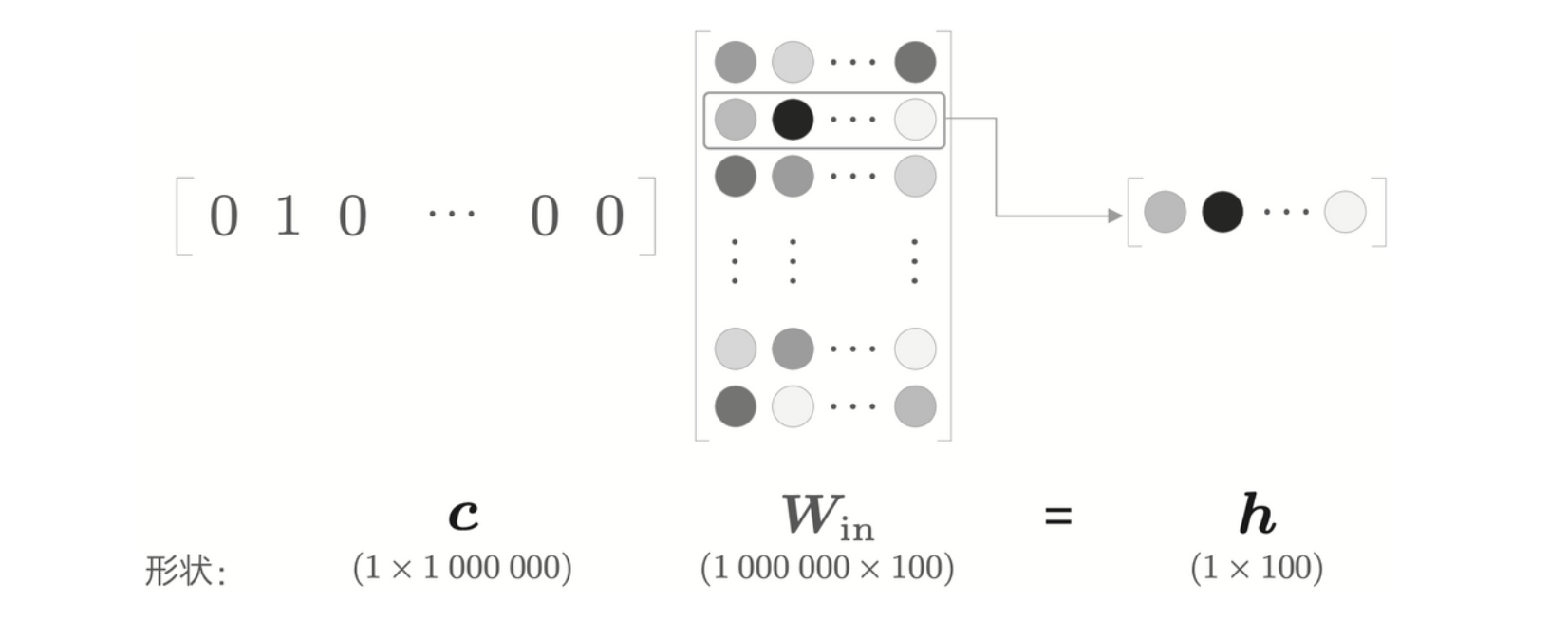
one-hot 表示的上下文和 MatMul 层的权重的乘积
其正向传播与反向传播如下所示
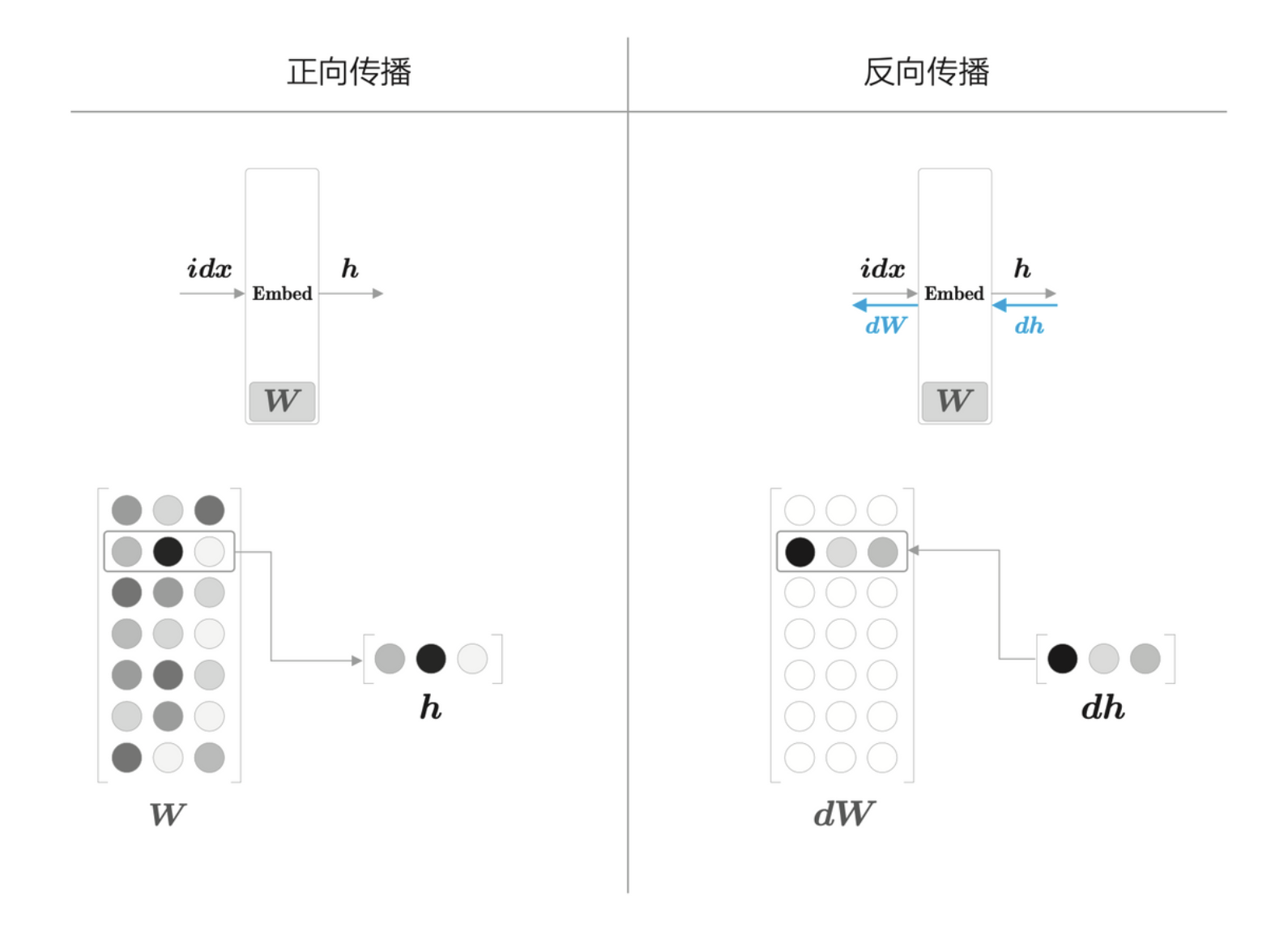
Embedding 层的正向传播和反向传播处理的概要
使用负采样
对 word2vec 的第二个优化在于优化矩阵乘积和 Softmax 层的计算。使用负采样(negative sampling)替代 Softmax,可以使得无论词汇量有多大,计算量都能保持较低或恒定。
考虑当词汇量非常大的时候,中间层往后的处理如下
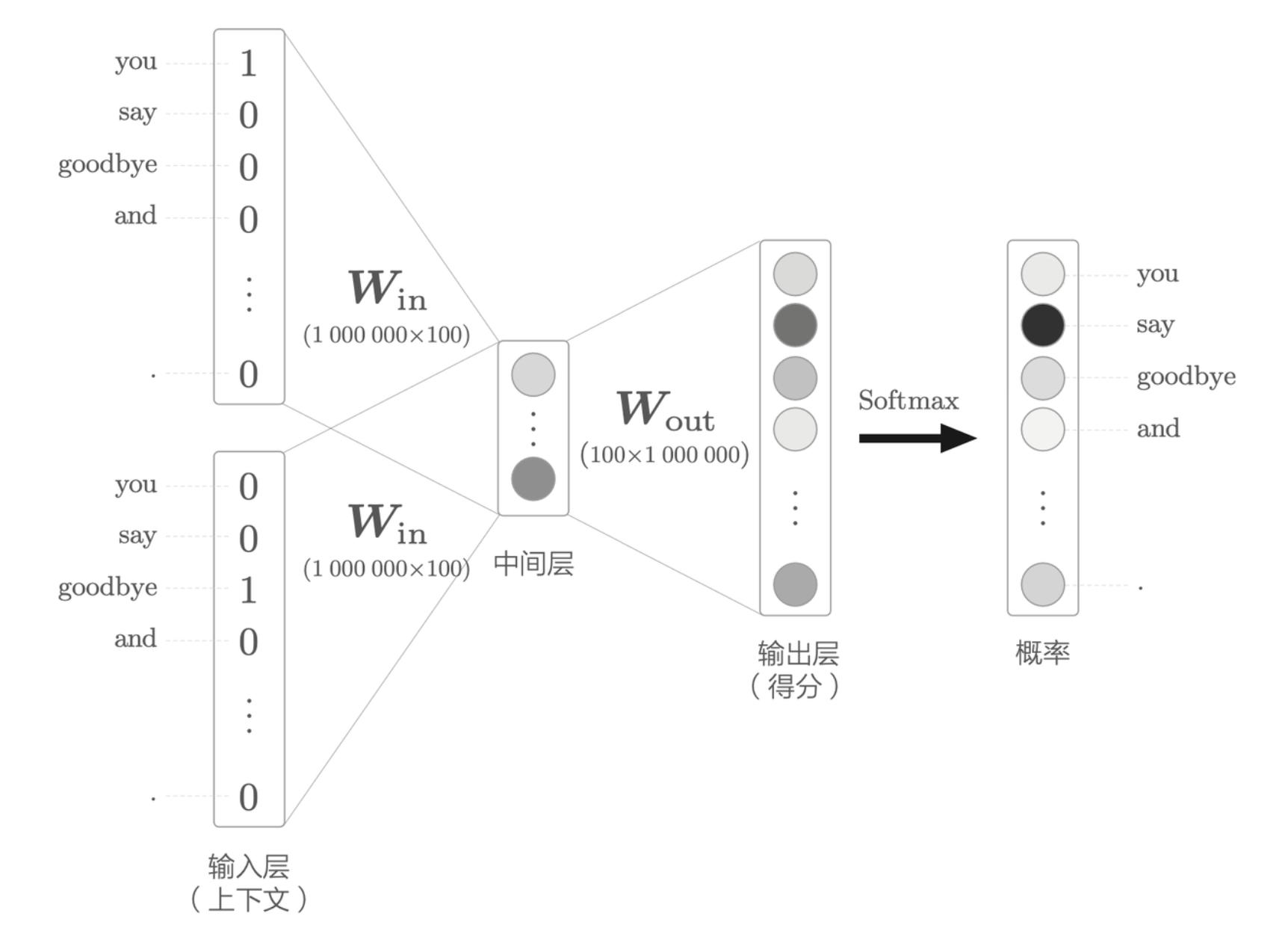
其中 \(\textbf{W}_{out}\) 的巨大矩阵乘积与词汇量成正比,另外,对于 Softmax 层来说,其中的第 \(k\) 个元素需要通过下式计算
\[ y_k = \frac{\exp(s_k)}{\sum_{i = 1}^{1000000} \exp(s_i)} \]
由此可见,对于每个词都得计算 1000000 次 \(\exp\),这是一个巨大的时间消耗,需要优化。
从多分类到二分类
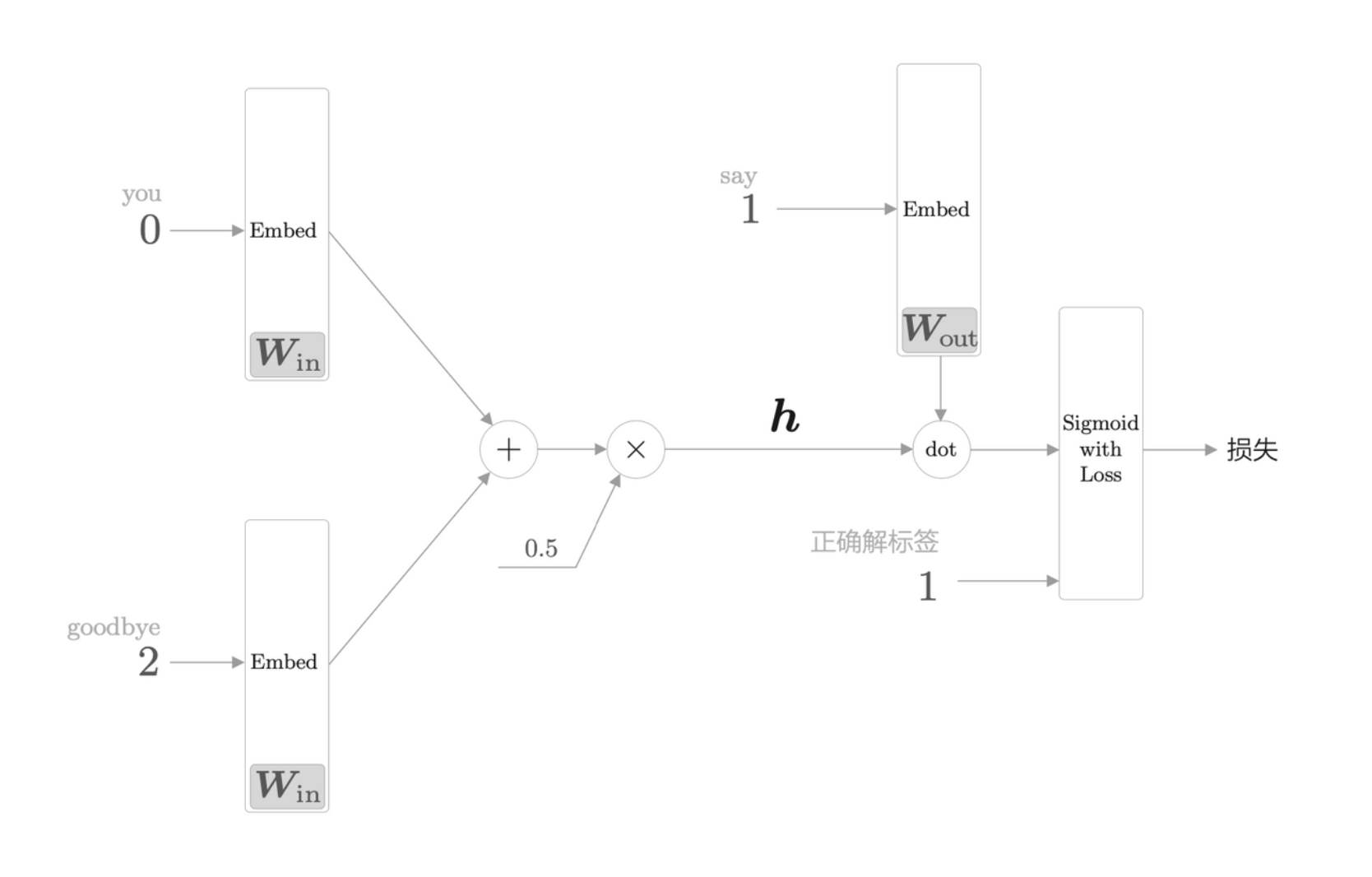
负采样的关键思想在于用二分类拟合多分类。从之前的例子中,我们回答的是概率问题,当给定 you 和 goodbye 时,神经网络预测单词为 say 的概率最高。如果我们改变问题,变成“当上下文是 you 和 goodbye 时,目标词是什么?”,这样,就将多分类问题转化为二分类问题。
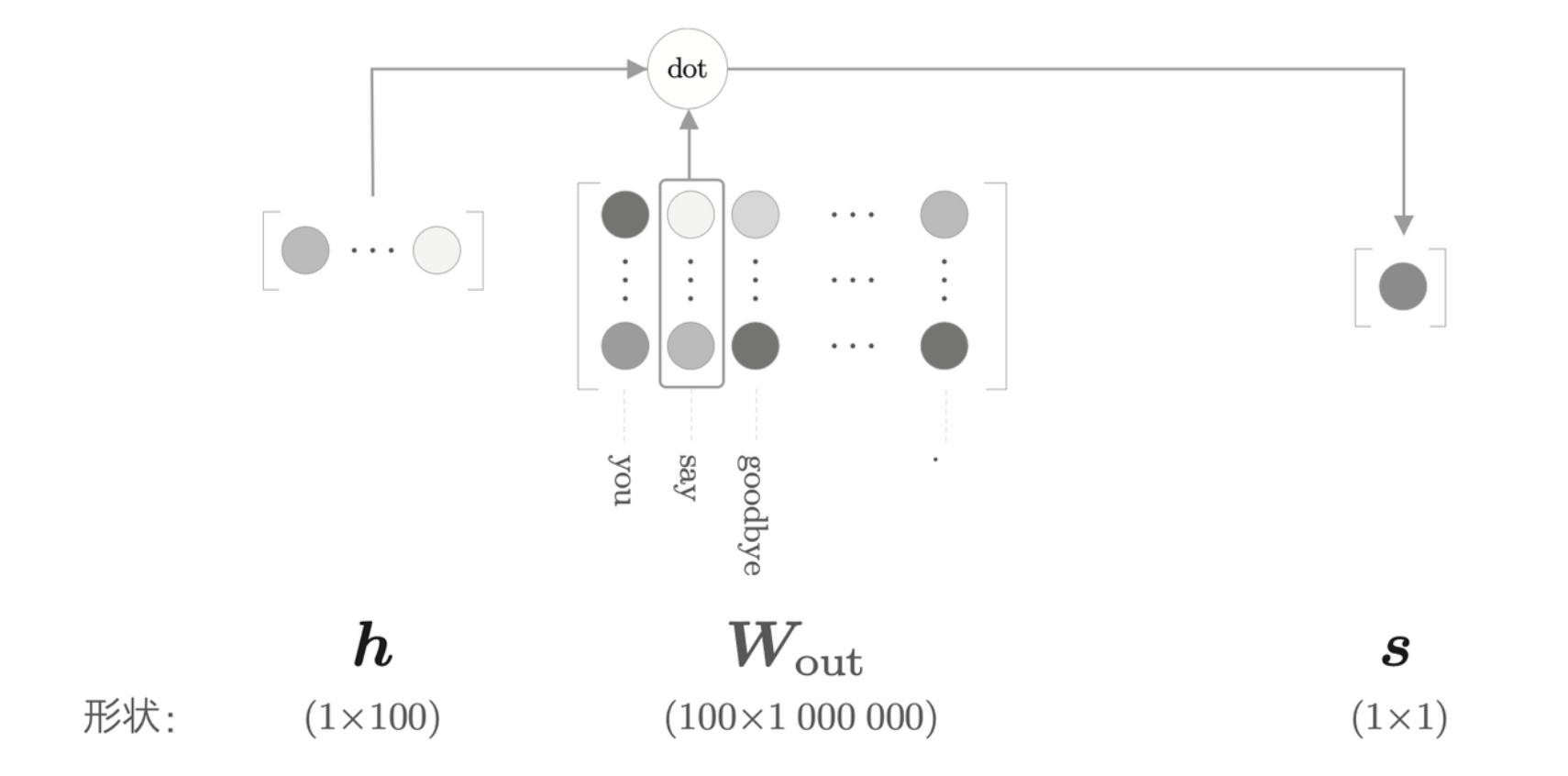
计算 say 对应的列向量和中间层的内积(图中的“dot”指内积运算)
Sigmoid 函数和交叉熵误差
对于多分类来说,使用 Softmax 计算概率,对于二元分类来说,使用 Sigmoid 函数计算概率,然后使用交叉熵计算误差。
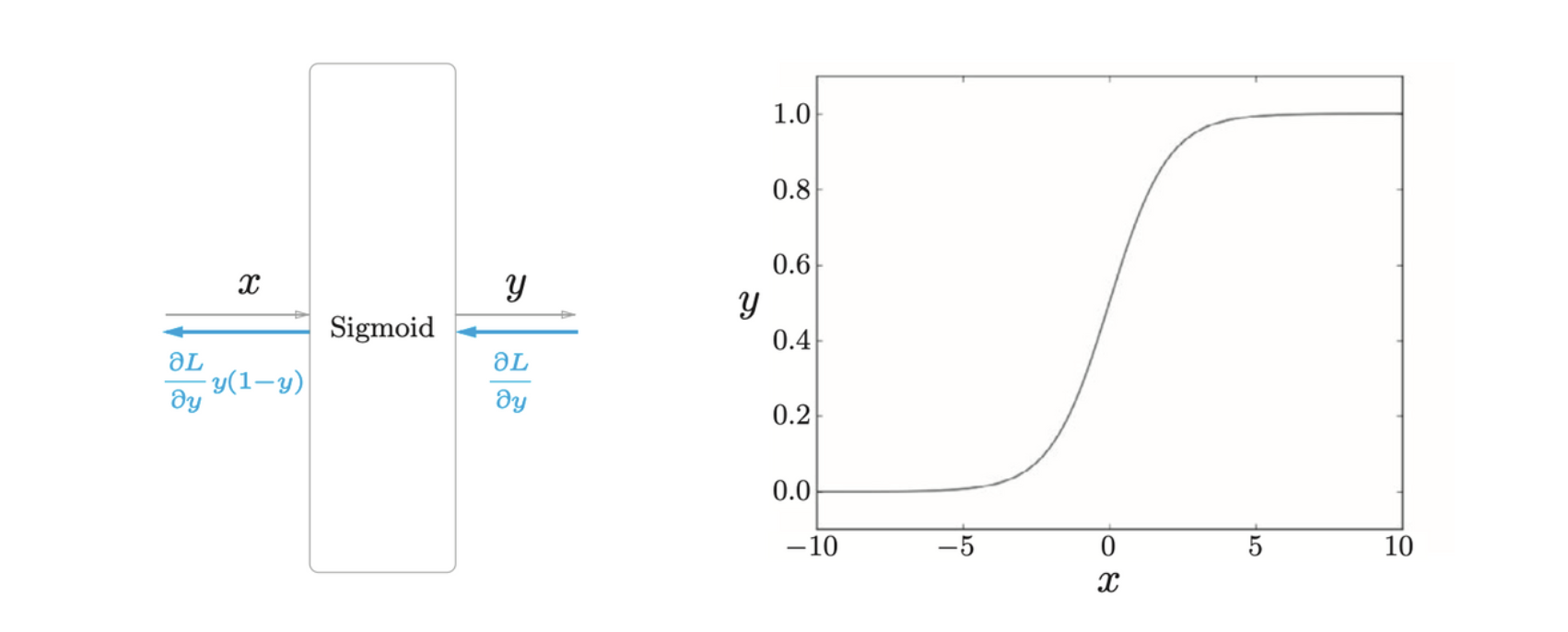
Sigmoid 层如上所示。从图可以看出,其输出值是一条从 0 到 1 的 S 型曲线,也可以解释为概率。通过 Sigmoid 函数得到概率 \(y\) 后,可以由 \(y\) 计算损失。与多分类一样,用于 Sigmoid 函数的损失函数也是交叉熵误差
\[ L = -(t \log y + (1 - t)\log(1 - y)) \]
其中 \(t\) 是正确解标签,取值为 0 或 1。当 \(t = 1\),输出 \(L = -\log y\),当 \(t = 0\),输出 \(L = - \log(1 - y)\)。下图为 Sigmoid 和 Cross Entropy Error 层的计算图,右图整合为 Sigmoid with Loss 层。
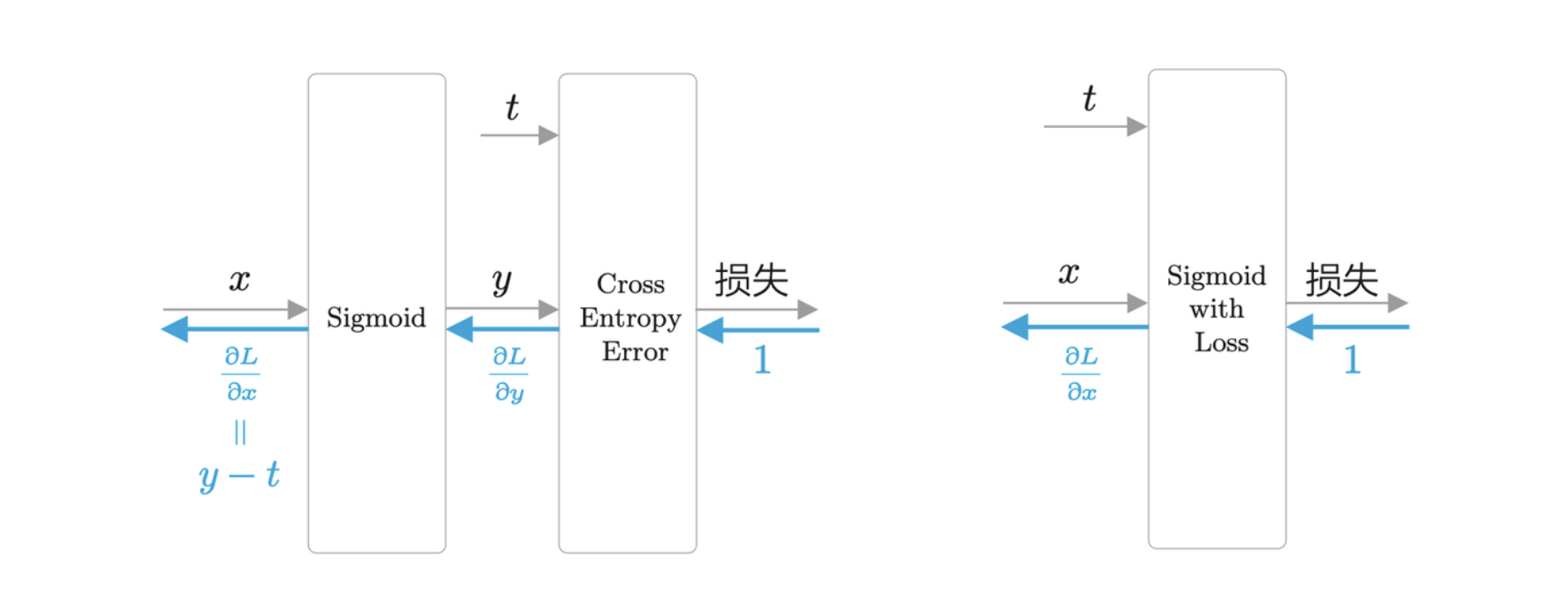
多分类到二分类的实现
综上,可以得到整个实现过程如何从多分类转变为二分类。