自然语言与单词的分布式表示
基于计数的方法
分布式假设
分布式假设(distributional hypothesis)是指,某个单词的含义是由它周围的单词形成。单词本身没含义,是由它所在的上下文形成。

窗口大小为 2 的上下文
共现矩阵
使用向量来表示单词最直接的方式是对周围的词的数量进行计数。这种方法称为“基于计数的方法”。比如上面的例子,假设窗口为 1,则可以得到如下的共现矩阵(co-occurance matrix)。
\[ \begin{vmatrix} & & \text{you} & \text{say} & \text{goodbye} & \text{and} & \text{i}& \text{hello} & \text{.} &\\ & \text{you} & 0 & 1 & 0 & 0 & 0 & 0 & 0 &\\ & \text{say} & 1 & 0 & 1 & 0 & 1 & 1 & 0 &\\ & \text{goodbye} & 0 & 1 & 0 & 1 & 0 & 0 & 0 &\\ & \text{and} & 0 & 0 & 1 & 0 & 1 & 0 & 0 &\\ & \text{i} & 0 & 1 & 0 & 1 & 0 & 0 & 0 &\\ & \text{hello} & 0 & 1 & 0 & 0 & 0 & 0 & 1 &\\ & \text{.} & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{vmatrix} \]
向量间的相似度
余弦相似度(cosine similarity)是比较常用的相似度算法。设有两个向量 \(\textbf{x}, \textbf{y}\),其相似度计算如下
\[ \text{similarity}(\textbf{x}, \textbf{y}) = \frac{\textbf{x} \cdot \textbf{y}}{|\textbf{x}||\textbf{y}|} = \frac{\sum\limits_{i = 0}^n x_i y_i}{\sqrt{\sum\limits_{i = 0}^n x^2}\sqrt{\sum\limits_{i = 0}^n y^2}} \]
改进
共现矩阵使用两个单词同时出现的次数,但是,这种次数并不具备好的性质。比如,某个语料库中 the 和 car 共现的情况。在这种情况下,会有很多 “… the car …” 这样的短语。另外,car 和 drive 也有很强的相关性,但是,如果只看出现次数,那么与 drive 相比,the 和 car 的相关性更强。
PPMI
为了解决这个问题,可以使用点互信息(Pointwise Mutual Information,PMI)这一指标。对于随机变量 \(x\) 和 \(y\),它们的 PMI 定义如下:
\[ \text{PMI}(x, y) = \log_2 \frac{P(x, y)}{P(x)P(y)} \]
在自然语言的例子中,\(P(x)\) 就是指单词 \(x\) 在语料库中出现的概率。可以使用共现矩阵表示上式,令共现矩阵为 \(\textbf{C}\),单词 \(x\) 和 \(y\) 的共现次数表示为 \(\textbf{C}(x, y)\), 将单词 \(x\) 和 \(y\) 的出现次数表示为 \(\textbf{C}(x), \textbf{C}(y)\),将语料库的单词数量标记为 \(N\),则上式可以重写为
\[ \text{PMI}(x, y) = \log_2 \frac{\frac{\textbf{C}(x, y)}{N}}{\frac{\textbf{C}(x)}{N}\frac{\textbf{C}(y)}{N}} = \log_2 \frac{\textbf{C}(x, y) \cdot N}{\textbf{C}(x)\textbf{C}(y)} \]
如果当两个单词的共现次数为 \(0\) 时,\(\log_2 0 = -\infty\)。为了解决这个问题,实践上我们会使用下面的正的点互信息(Positive PMI,PPMI)
\[ \text{PPMI} = \max(0, \text{PMI}(x, y)) \]
降维
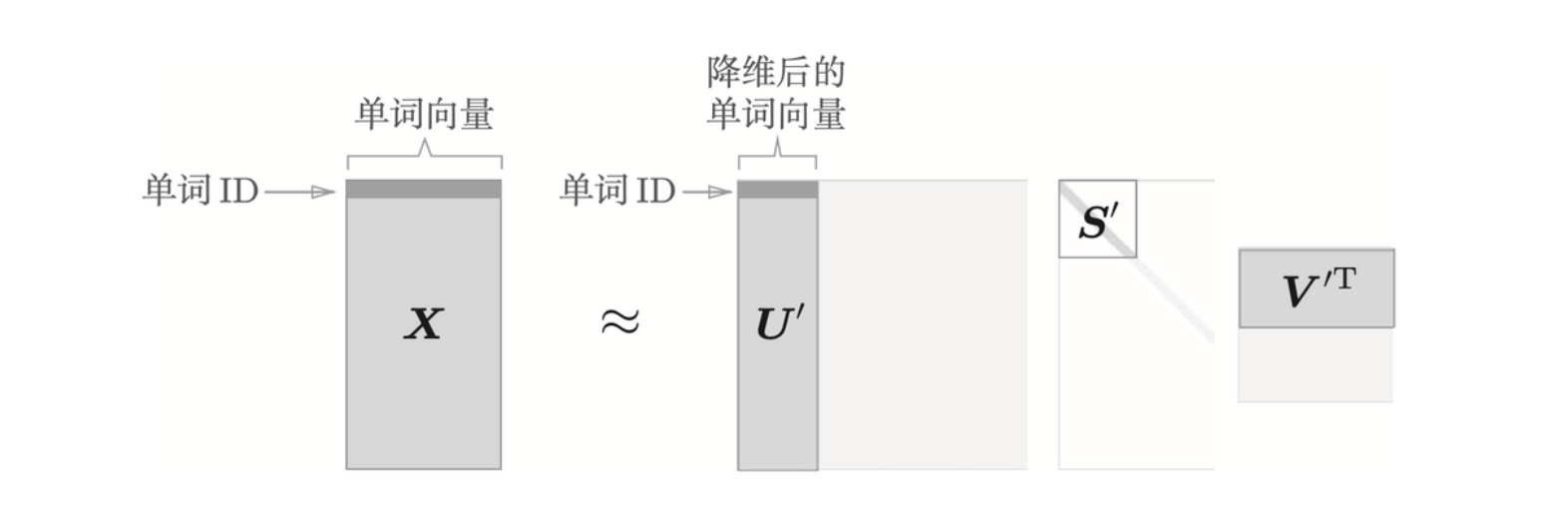
降维的方法有很多,这里我们使用奇异值分解(Singular Value Decomposition, SVD)。SVD 将任意矩阵分解为 3 个矩阵的乘积,如下所示:
\[ \textbf{X} = \textbf{U}\textbf{S}\textbf{V}^T \]
其中 \(\textbf{U}\) 和 \(\textbf{V}\) 是列向量彼此正交的正交矩阵,\(\textbf{S}\) 是除了对角线元素以外其余元素均为 0 的对角矩阵。