集异璧之大成

发表于 分类于 Disqus： 本文字数： 7.3k 阅读时长 ≈ 27 分钟
集异璧之大成
Hofstadter
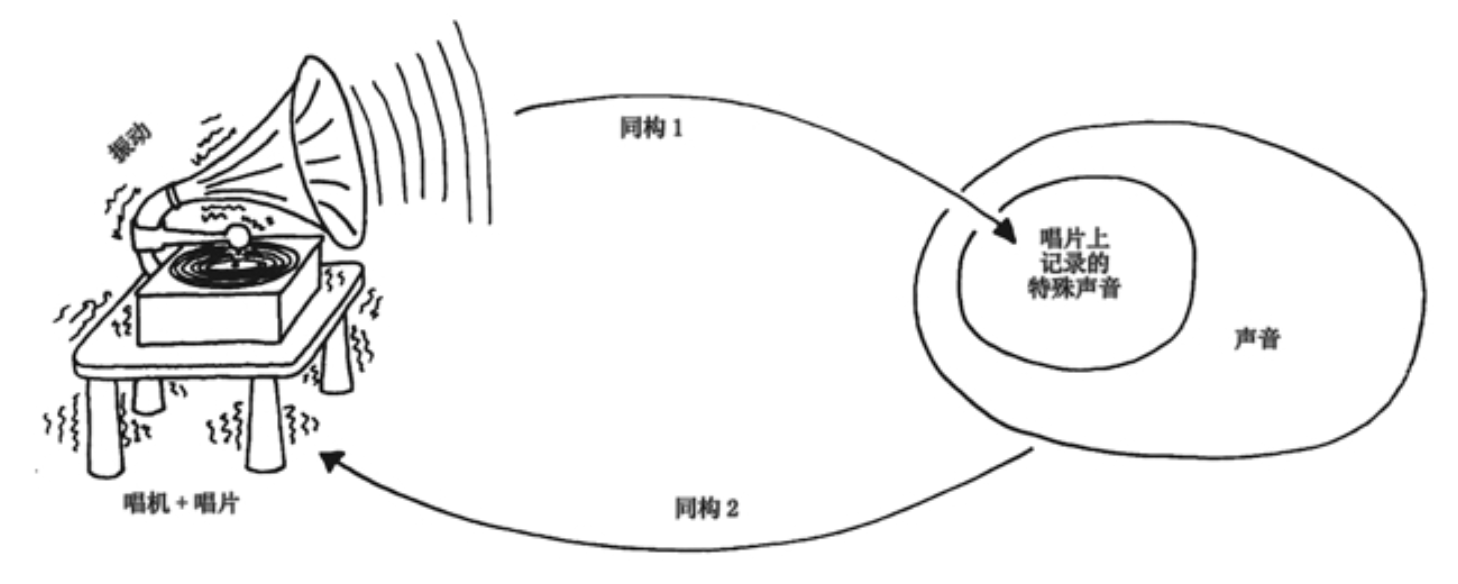
哥德尔定理背后的原理的形象化表现

哥德尔定理背后的原理的形象化表现

两个映射背靠背具有了出乎意料的飞去来器效果。第一个映射是从纹道模式到声音，由一个唱机实现。第二个——很平常，但却常常被忽视——是从声音到唱机的震颤。注意第二个映射独立于第一个映射而存在，因为附近的任何声音——不仅是唱机自己产生的声音——都会引起这种震颤。哥德尔定理转述在这里就是：对任何一个唱机，都有它不能播放的唱片，因为后者会导致前者的间接自摧毁。

上图与哥德尔定理之间的映射

\[ \begin{align} 唱机 &\iff 数论的公理系统 \\ 低保真唱机 &\iff “弱”公理系统 \\ 高保真唱机 &\iff “强”公理系统 \\ “完备的”唱机 &\iff 数论的完全系统 \\ 唱机的图纸 &\iff 形式系统的公理与规则 \\ 唱片 &\iff 形式系统的符号串 \\ 可以播放的唱片 &\iff 公理系统的定理 \\ 不能播放的唱片 &\iff 公理系统的非定理 \\ 声音 &\iff 数论的真陈述 \\ 可重现的声音 &\iff 系统中经过解释了的定理 \\ 不可重现的声音 &\iff 非定理的真陈述 \\ \end{align} \]

一致性：每个定理经解释后都成为真的（在某个想象的世界里）。

完全性：所有真的（在某个想象的世界里）且可表示成系统中的良构符号串的陈述都是定理。

哥德尔不完全性定理说的是任何“足够强有力”的系统，由于起能力较强，因而是不完全的。即：存在良构的字符串，表示了数论中的真陈述，但不是定理。

意义位于何处

消息

消息分为三个层面

  1. 框架消息
  2. 外在消息
  3. 内在消息

框架消息是这样的一种消息：“我是一条消息，你有本事就来解释我”它是由信息携带者总体的结构特征隐含传递的。

外在消息，有信息中的符号模式及结构隐含地携带的信息，说明如何去解释内在消息。

在理解任何一条消息之前，你必须有另一条消息来告诉你如何理解这条消息，换句话说，存在一个具有无穷多层次的消息体系，这就阻止了对任何消息的理解。

命题演算

形式系统定义

符号表：

\[ \{ <, >, P, Q, R, ', \land, \lor, \to, \sim, [, ] \} \]

原子：\(P, Q, R\) 都称作原子，新的原子是在老的原子的右上角加撇构成，比如 \(P', Q', R''\) 等。所有原子都是良构的。

形成规则：如果 \(x\) 和 \(y\) 都是良构的，那么以下四种串也是良构的：

  1. \(\sim x\)
  2. \(<x \land y>\)
  3. \(<x \lor y>\)
  4. \(<x \to y>\)

联结规则：如果 \(x\) 和 \(y\) 都是系统的定理，那么串 \(<x\land y>\) 也是该系统的定理。

分隔规则：如果 \(<x \land y>\) 是一个定理，那么 \(x\) 和 \(y\) 都是定理。

双重弯号规则：\(\sim \sim\) 可以从任何定理中删去，也可以嵌入任何定理中，条件是所得的结果是良构串。

幻想规则：令 \(x\) 为幻想的前提，然后通过遵循系统的规则的推导，得到幻想的结果 \(y\)。那么“假如 \(x\) 是一个定理，那么 \(y\) 就会是一个定理”。

搬入规则：在一个幻想里，任何来自“现实性”高一个层次的定理都可以拿进并使用。

分离规则：如果 \(x\) 和 \(<x \to y>\) 两者都是定理，那么 \(y\) 是一个定理。

易位规则：\(<x \to y>\) 与 \(<\sim x \to \sim y>\) 是可互换的。

德·摩根规则：\(<\sim x \land \sim y>\) 与 \(\sim<x \lor y>\) 是可互换的。

思维陀螺规则：\(<x \lor y>\) 与 \(<\sim x \to y>\) 是可互换的。（有点像程序语言里的逻辑短路）

幻想规则例子

[       推入幻想
    P     前提
    ~~P   结果（根据双重弯号规则）
]       弹出幻想

这个幻想说明：假如 \(P\) 是一个定理，那么 \(\sim \sim P\) 也是一个定理。使用符号来表示便是 \(<P \to \sim \sim P>\)

[           推入幻想
    <P^Q>     前提
    P         分隔
    Q         分隔
    <Q^P>     联结      
]           弹出幻想

由此得到的幻想规则是 \(<<P \land Q> \to <Q \land P>>\)

搬入规则的例子

[               推入
    P             外层幻想的前提
    [             再次推入
        Q           内层幻想的前提
        P           把 P 搬入内层幻想
        <P^Q>       联结
    ]             弹出内层幻想，回到外层幻想
    <Q→<P^Q>>     幻想规则
]               弹出
<P→<Q→<P^Q>>>   幻想规则

印符数论

TNT（Topographical Number Theory）。使用形式系统表达数论。

系统定义

数字

数字使用后继的记法，也就是

零：0

一：S0

二：SS0

三：SSS0

变元和术语

使用字母表达变元，字母不够的时候可以加撇

运算

运算只定义加法和乘法，用常规的记号进行。比如 b + c，b x c。

原子与命题符号

命题验算中的所有符号，除了用于构成原子的字母 P，Q，R 之外，都在 TNT 中使用。原子的角色将由这样的串来充当：当它们解释出来时，是一些关于相等的陈述。比如 S0 = SS0 或 ~(SS0 + SS0) = SSS0 等。

自由变元和量词

存在自由变元的良构公式不具备真假性，比如 (b + S0) = SS0。因为 b 未指定，所以不能表达出真假。但如果加上全称量词 \(\forall\) 或者存在量词 \(\exists\)，则具备了真假性。

TNT 的五条公理

上面的定义只能不断通过规则构造出良构串，然而是否能通过印符系统来给出真描述的规则呢？先从五个公理入手。

\[ \begin{align} 公理1 &: \forall a: \sim Sa = 0 \\ 公理2 &: \forall a: (a+0) = a \\ 公理3 &: \forall a: \forall b: (a + Sb) = S(a + b) \\ 公理4 &: \forall a: a \cdot 0 = 0 \\ 公理5 &: \forall a: \forall b: (a \cdot Sb) = ((a \cdot b) + a) \\ \end{align} \]

TNT 新规则

特称规则与概括规则，将全称量词取消并且加回，互换规则提供全称量词与存在量词的互换。

特称规则

假设 \(u\) 是一个出现在串 \(x\) 中的变元，如果串 \(\forall u: x\) 是一个定理，则 \(x\) 也是定理。并且，对 \(x\) 中的 \(u\) 做任何替换得到的串同样是定理。

概括规则

假设 \(x\) 是一个定理，其中的变元 \(u\) 是自由出现的，那么 \(\forall u : x\) 是一个定理。

互换规则

假设 \(u\) 是一个变元，那么串 \(\forall u: \sim\) 与 \(\sim \exists u:\) 在任何定理中的任何地方都是可以互换的。

存在规则

假设一个项（可以含有变元，只要是自由的）在一个定理中出现一次或多次，那么，这个项的任何（或者是一些，或者是所有）出现都可以用一个不在定理中出现的变元来替代，相应的存在量词则必须放在最前面。

等号规则

对称：如果 \(r = s\) 是一个定理，那么 \(s = r\) 同样也是定理。

传递：如果 \(r = s\) 和 \(s = t\) 都是定理，那么 \(r = s\) 也是定理。

后继规则

加 \(S\)：如果 \(r = t\) 是一个定理，那么 \(Sr = St\) 是一个定理。

去 \(S\)：如果 \(Sr = St\) 是一个定理，那么 \(r = t\) 是一个定理。

\(\omega\) 不完全系统

比如，在 TNT 系统中可以推导出下面的金字塔串

\[ (0 + S0) = S0 \\ (0 + SS0) = SS0 \\ (0 + SSS0) = SSS0 \\ (0 + SSSS0) = SSSS0 \\ \]

但其全称量词化的串

\[ \forall a: (0 + a) = a \]

却不能通过规则推导出来。这意味着，这个串在系统里是不可判定的。这种不一致性的产生是由于下面两件事的对立

  1. 一个由一些定理组成的金字塔，它们集合起来断言所有的自然数具有某种性质。
  2. 一个单个的定理，它看上去是断言并非所有的自然数具有该性质。

这种不一致性成为 \(\omega\) 不一致性。一个 \(\omega\) 不一致的系统更像一个被人们“初拒后纳”的非欧几里得几何。这意味着：迄今所介绍的 TNT 的公理和规则并没有完全固定住对 TNT 符号的解释。

二元论

顿悟

所谓顿悟，最简明扼要地说或许就是：超越二元论。二元论是指把世界从概念上划分为种种范畴。二元论不仅是概念上对世界的划分，同样也是感知上对世界的划分。

禅宗来看，二元论的核心就是词语——普通的词。对词的使用必然导致二元化，因此每个词很明显地就代表了一个概念范畴。所以，禅宗的一个主要部分就是反对依靠词语而斗争。

如果依赖词语走向真理，那就如同一个依赖一个不完全的形式系统而走向真理。一个形式系统的确会给你一些真理，但是无论一个形式系统多么强有力，都不可能给出所有真理。

摒弃感知，摒弃逻辑，词语，二元化的思维——这就是禅宗的实质，主义的实质。禅宗采纳整体论，并且推向逻辑上的极端。如果整体论是断言事物必须作为一个整体被理解，而非其各个部分的总和，那么禅宗走的更远，认为整个世界根本就不能被划分为一个个事物。划分世界就会侮辱歧途，因而就不能达到顿悟了。

哥德尔配数

若有一条印符规则，它在任一十进制表示的数中移动，改变，删除或插入数码，那么这条规则可由同样的一条算术规则来替代，后者包括对 10 的方幂的算术运算以及加，减等运算。

一旦对一个形式系统进行了哥德尔配数，立刻就有了一组规则，使我们得到完整的哥德尔同构。结果就是，我们可以把对任一形式系统的研究——事实上即对所有形式系统的研究——转成数论工作。

当把形式系统研究转换成数论研究时，就会产生这类问题，对每个算数话的系统都可以问，“我们能否用一种递归可枚举的办法刻画不可产生的数？”

对 TNT 进行哥德尔配数

对 TNT 的符号进行哥德尔配数，然后将其推理规则“算术化”。下面是一些对应关系。

\[ \begin{vmatrix} 符号 &\ \ \ \ \ \ \ 密码子 \\ 0 &\ \ \ \ \ \ \ 666 \\ S &\ \ \ \ \ \ \ 123 \\ = &\ \ \ \ \ \ \ 111 \\ + &\ \ \ \ \ \ \ 112 \\ \cdot &\ \ \ \ \ \ \ 236 \\ ( &\ \ \ \ \ \ \ 362 \\ ) &\ \ \ \ \ \ \ 323 \\ < &\ \ \ \ \ \ \ 212 \\ > &\ \ \ \ \ \ \ 213 \\ [ &\ \ \ \ \ \ \ 312 \\ ] &\ \ \ \ \ \ \ 313 \\ a &\ \ \ \ \ \ \ 262 \\ ' &\ \ \ \ \ \ \ 163 \\ \land &\ \ \ \ \ \ \ 161 \\ \lor &\ \ \ \ \ \ \ 616 \\ \to &\ \ \ \ \ \ \ 633 \\ \sim &\ \ \ \ \ \ \ 333 \\ \exists &\ \ \ \ \ \ \ 626 \\ \forall &\ \ \ \ \ \ \ 636 \\ : &\ \ \ \ \ \ \ 611 \\ \end{vmatrix} \]

每个 TNT 符号都与由 1、2、3 和 6 组成的一个三位数配对，配对原则只是有助于记忆。公理的记法将进行如下转换

\[ \begin{align} \forall & a & : & \sim & S & a & = & 0 \\ 626 & 262 & 636 & 223 & 123 & 262 & 111 & 666 \end{align} \]

这样看来，对于定理的推导就是一系列高度曲折的数论变换，每个变换都作用在一个或多个作为输入的数之上，给出输出的数。这些产生出来的数，称为 TNT 数。

这种对 TNT 的“哥德尔化”引出了一个新的数论谓词：

\[ \text{a 是个 TNT 数} \]

我们如果在前面加一个弯号，得到的串表示一个互补的命题：

\[ \text{a 不是一个 TNT 数} \]

如果我们把所有 a 都替换成与 123，666，111，666 相应的 TNT 数码，我们会得到一个 TNT 串，它可以从两个层次上来解释。首先，这个串说的是

\[ \text{123, 666, 111, 666 不是个 TNT 数} \]

但因为有一个连结 TNT 数与 TNT 定理的同构，这个串还有第二层含义，就是

\[ \text{S0 = 0 不是 TNT 的定理} \]

这个双重性证实了 TNT 中有谈论其他 TNT 串的符号串。换句话说，我们在外面用于谈论 TNT 的元语言，多少是部分地在 TNT 内部遭到了模仿。这种事情之所以发生，是因为任何形式系统的构建都可以在 N（数论） 中得到反映。是数论的形式化的本质导致其元语言嵌在其自身中。这一看法被冠以“数理逻辑的中心法则”，用一个两步的图解来描述。

\[ \text{TNT} \to \text{N} \to \text{元 TNT} \]

TNT 的一个串有一个 N 中的解释，而 N 中的一个陈述可以有一个第二意义，即作为 TNT 的陈述。

论 TNT 及有关系统中形式上不可判定的命题

两个关于哥德尔定理证明的核心想法

  • 某些 TNT符号串能解释成在谈论另一些 TNT 符号串，这是哥德尔配数的产物。
  • 这种自我审视的性质可以全部集中于一个单个的符号串，于是这个符号串所注视的唯一交点就是它自己了。本质上，这种“聚焦手法”可以上溯到康托尔的对角线方法。

证明对

一个证明对是一对以某种特殊方式结合在一起的自然数。这里的想法是：

实际上是构造了一种映射，将整个推导过程（推导过程必须是合法的）进行哥德尔数编码，得到 \(m\)，然后 \(n\) 为推导的最后一行，也就是推导结果。比如在 WJU 系统中，令 \(m = 3131131111301\)，\(n = 301\)，因为存在推导

WJ // 31
WJJ // 311
WJJJJ // 31111
WUJ // 301

m = 3131131111301
n = 301

所以 \(m\) 和 \(n\) 构成了一个证明对。

“是证明对”是原始递归的

这和另一个密切相关的数论性质——“是定理数”——有个值得注意的对比。要断定 \(n\) 是一个定理数，就是要断定存在某个 \(m\) 能与 \(n\) 形成证明对，所以这有可能将要进行一场无穷尽的追寻。

一个更强有力的形式系统

TNT 的弱点何在？本质上就是在于它能表示自指陈述——具体说，就是陈述“我在形式系统 TNT中不可证”。或者，“没有一个自然数与本符号串的哥德尔数形成 TNT 证明对”。

在一个给定的系统中，是否可能利用哥德尔的自指方法构造一个不可判定的符号串，依赖于三个基本条件：

  1. 该系统要足够丰富，一遍全部所需要的有关数的陈述，无论真假，都能在其中表示。（做不到这一点，就意味着形式系统从一开始就弱得不能与 TNT 匹配，因为它连 TNT 能表示的那些数论概念都表示不了。）
  2. 所有的一般递归关系都能用该系统的公式体现。（做不到这一点，就意味着该系统不能用定理来把握一般递归的真理，也就是说，这种系统是不能用来产生数论中的全部真理的。）
  3. 公理以及根据该系统的规则所确定的印符模式，都能通过某个有终止的过程来辨认。（做不到这一点，就意味着无法区分该系统中的有效推导和无效推导——因而该“形式系统”根本就不是形式化的，更谈不上是良定义的了。）

满足了这三个条件，就保证每个一致的系统都不完全，因为哥德尔的构造能得以实施。系统本身的丰富性使其垮台，由于该系统强得能有自指句子，这种垮台现象就不可避免。

印符遗传学

基础概念

串，基，酶

使用四个字母，A，C，T，G，这四个字母可以组成一些串，GGGG，ATTACCA 等。在遗传学中，这些串为 DNA 片段。

可以对串进行一些操作，可以想象一台程序化的机器在串上移来移去施加操作，这些活动着的机器称为“印符酶”，简称酶。有四种酶，喜欢 A 的酶，喜欢 C 的酶等等。假设一个酶由三项操作构成：

  1. 删除拴着这个酶的单元（并把酶往右移动一个单元）
  2. 向右移动一个单元
  3. 在当前单元右边插入一个 T

那么这个酶的作用就是将 ACA 变为 CAT。

复制状态

复制一个串的时候，并不是直接复制它，而是产生出它的补串。

氨基酸

总拥有十五种类型

  • cut —— 切断串
  • del —— 从串里删除一个基
  • swi —— 把酶转移到另一个串上
  • mvr —— 右移一个单元
  • mvl —— 左移一个单元
  • cop —— 进入复制状态
  • off —— 退出复制状态
  • ina —— 在本单元右侧插入 A
  • inc —— 在本单元右侧插入 C
  • ing —— 在本单元右侧插入 G
  • int —— 在本单元右侧插入 T
  • rpy —— 寻找右边最近的嘧啶
  • rpu —— 寻找右边最近的嘌呤
  • lpy —— 寻找左边最近的嘧啶
  • lpu —— 寻找左边最近的嘌呤

于是，每个酶都由一系列的氨基酸制成。比如

\[ rpu - inc - cop - mvr - mvl - swi - lpu - int \]

这个氨基酸，作用在串 TAGATCCAGTCCATCGA 上的时候，如果这个酶从中间的 G 开始操作，最终会得到两个串，ATC 和 TAGATCCAGTCCATCGA。

印符遗传密码

一个串中各对相邻的基——称作“二元组”——表示各种不同的氨基酸，总共有 16 种可能的二元组：AA，AC，AG，AT，CA，CC 等，而氨基酸共有 15 种。

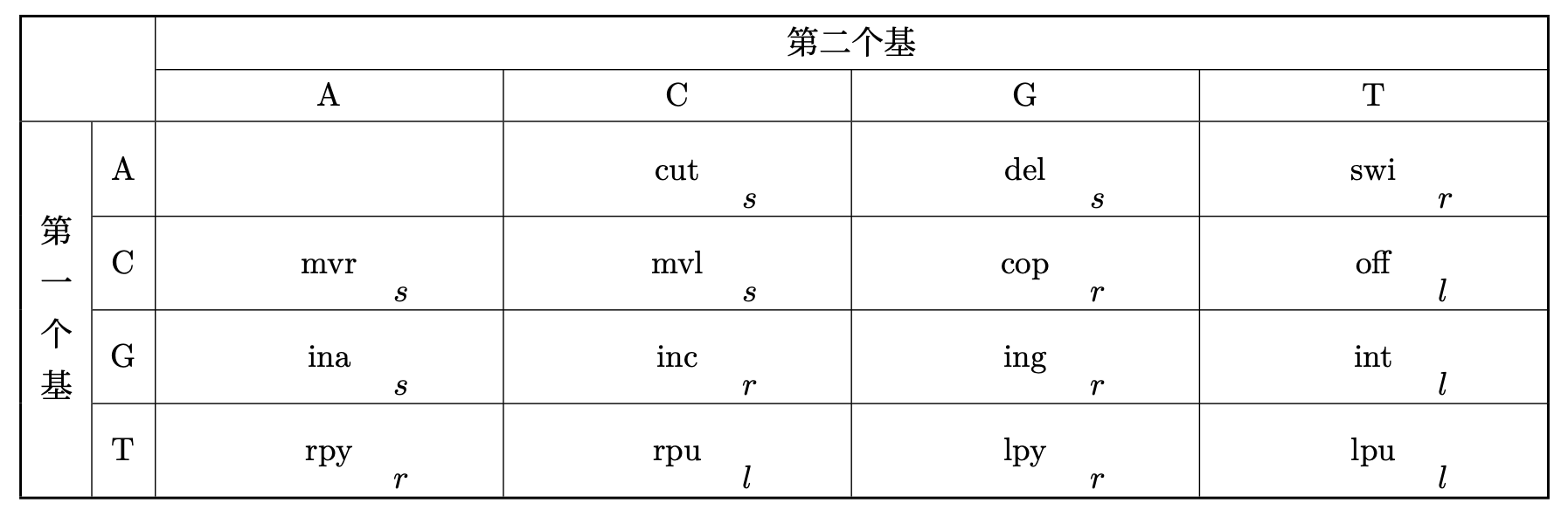
按照这个表，一个串便能口述成一种酶了。例如串

TAGATCCAGTCCACATCGA

分解成二元组就是

TA GA TC CA GT CC AC AT CG A

翻译成酶就是

rpy-ina-rpu-mvr-int-mvl-cut-swi-cop

剩下的 A 没什么用处。

酶的三级结构

一级结构指的是氨基酸序列，而三级结构指的是其折叠方式。表中的下标含义为

  • l：左
  • r：右
  • s：直

用上面的酶做例子，其三级结构为

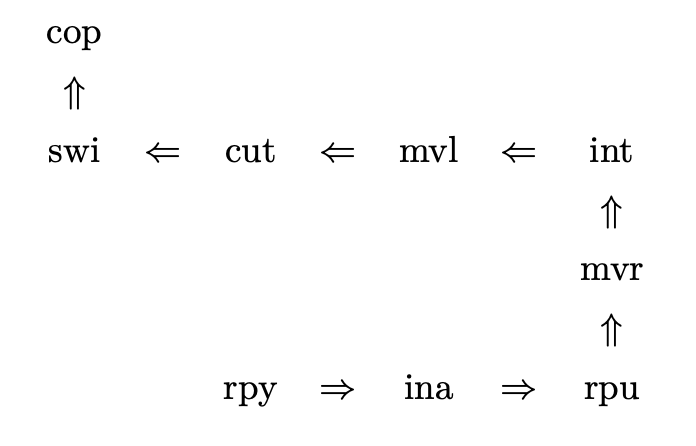
在酶的三级结构中，第一段和最后一段的相对方向决定了酶应该拴在什么地方。我们总能调整酶的方向，使其第一段指向右方，如果这样做了，那么最后一段就决定了酶所栓的位置。

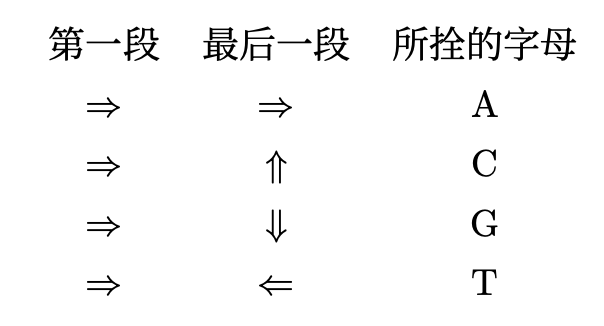
标点，基因与核糖体

印符遗传密码 AA 起到标点的作用，比如串

CG GA TA CT AA AC CG A

就是两个酶编码，分别是

cop-ina-rpy-off 和 cut-cop

AA 把该串分成了两个”基因“。基因的定义是：一个串中给一个酶编码的那个部分。

读串并产生出它们编码的酶，这种装置称为核糖体。

印符遗传学的自复制

通过一个初始串，核糖体作用在其上面，就产生出该串编码的所有酶。然后让这些酶接触原本的串，得到一批”子串“。这些子串又通过核糖体的作用得到第二代酶，这些酶作用在子串上，如此循环往复。问题是：最终，在某一代里，能找到最初那个串的两个副本吗？

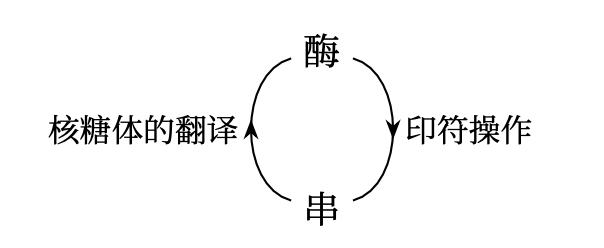
DNA 与核苷酸

DNA 由两条核苷酸长链构成，而一个核苷酸由三部分构成

  1. 脱去一个特殊氧原子的，称为”核糖“的一种糖
  2. 磷酸基
  3. 一个基

区别各种核苷酸的东西只是这个”基“，出现在 DNA 核苷酸中的四种类型的基是

  • A：腺嘌呤
  • G：鸟嘌呤
  • C：胞嘧啶
  • T：胸腺嘧啶

其中 A-T 配对，C-G 配对。

信使 RNA 与核糖体

细胞核内有一种特殊类型的酶把 DNA 序列中的一个长段复制到一个新串 —— 信使 RNA 串（mRNA） —— 上。然后，这个 mRNA 离开细胞核，在细胞质中跑进核糖体内，这些核糖体再根据这个 mRNA 来制造酶。在细胞核内把 DNA 复制到 mRNA 上的过程叫转录。

RNA 为”核糖核酸“，其核苷酸里都包含 DNA 核苷酸所缺的那个氧原子。另外 RNA 用尿嘧啶这个基，没有胸腺嘧啶。转录的过程为

氨基酸

蛋白质由一系列的氨基酸组成。

核糖体

当一个 mRNA 游离出来进入细胞质，然后遇到一个核糖体的时候，就会发生翻译的过程。这个翻译过程是一切生命的根本所在。

每三个核苷酸编码一个氨基酸，编码表与印符遗传密码类似，只是数量更多罢了。核糖体每三个三个地读核苷酸，然后生成一个新的氨基酸，并把这个氨基酸加到正在生产的蛋白质上。由此，蛋白质就在核糖体内被制造出来了。

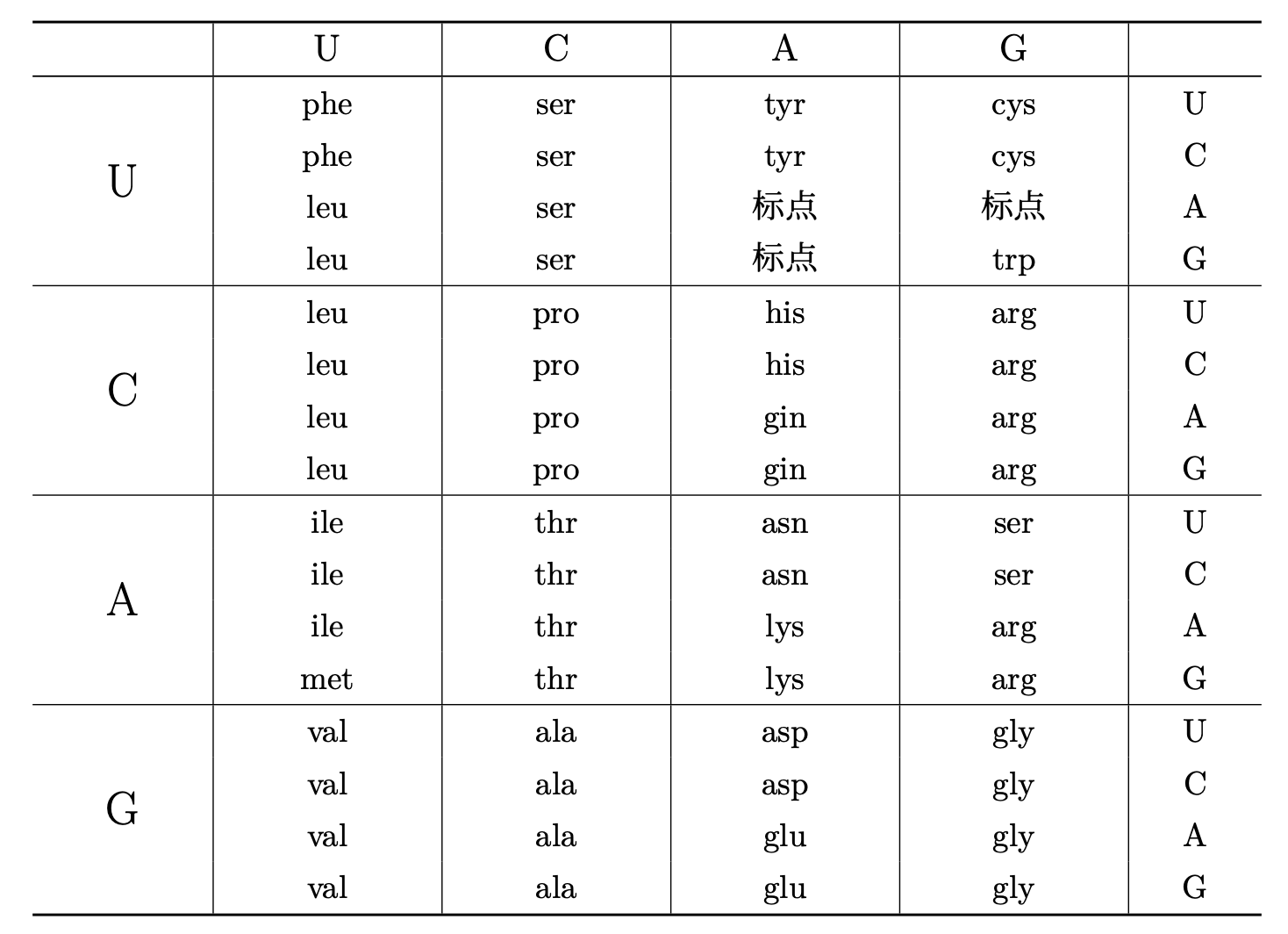
遗传密码。信使RNA串中的每个三元组就这样为二十种氮基酸(及一个标点符号)编码。
从一些高分辨率的X光资料推断出的肌红蛋白的结构。大尺寸的“扭曲管道”形状是三级结构，内部的细螺旋——“阿尔法 螺旋”——是二级结构。
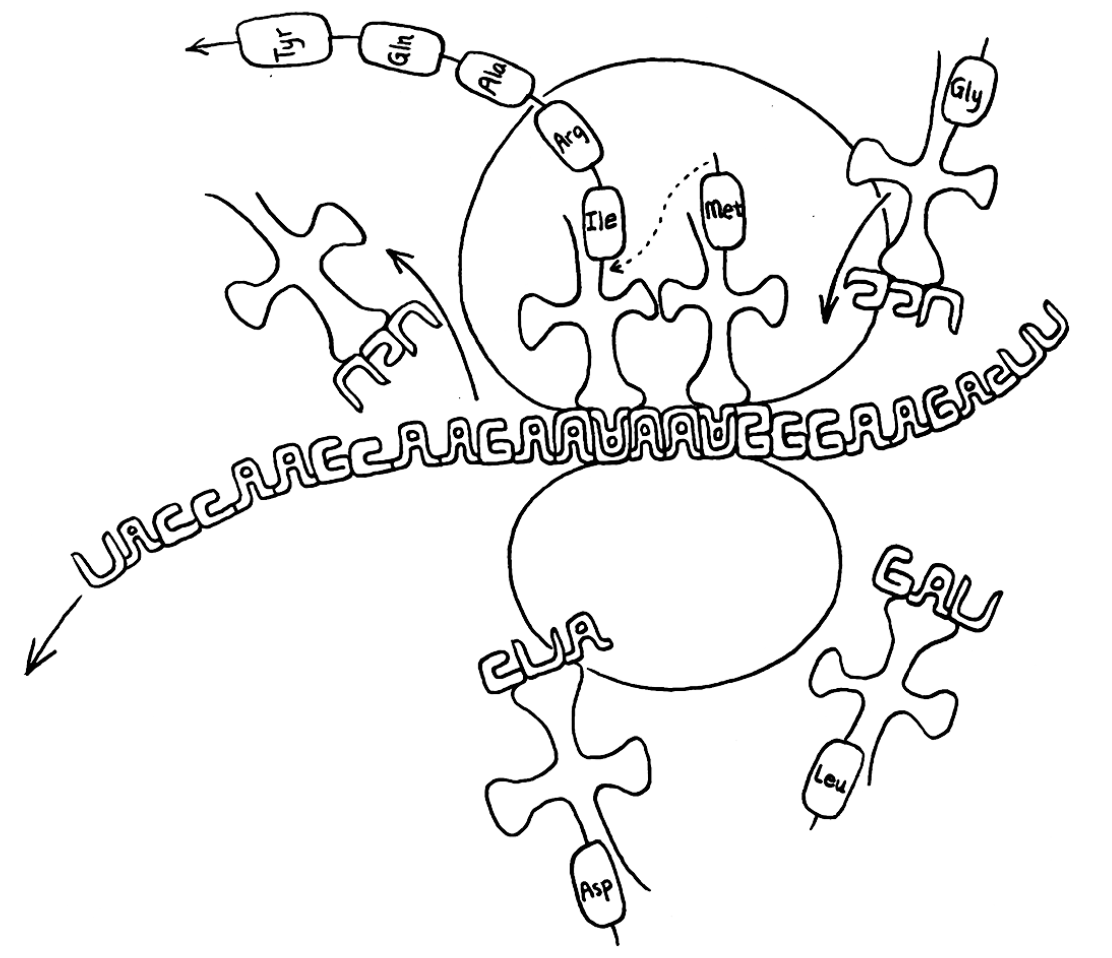
一段 mRNA 通过核糖体。漂浮在附近的是些 tRNA 分子，它们带有能被核糖体抓来并加进正在生成的蛋白质中的氨基酸。 遗传密码作为一个整体包含在 tRNA 分子内。要注意，基对(A-U，C-G)在图中由卡在一起的字型表示。

一段 mRNA 通过核糖体。漂浮在附近的是些 tRNA 分子，它们带有能被核糖体抓来并加进正在生成的蛋白质中的氨基酸。 遗传密码作为一个整体包含在 tRNA 分子内。要注意，基对(A-U，C-G)在图中由卡在一起的字型表示。

细胞质周围漂浮着大量的“四叶草”（如上图），在其中一个叶片上拴着一个氨基酸，氨基酸对面的叶片上有一个成为反密码子的核苷酸三元组。当 mRNA 进入核糖体的时候，核糖体会吸收一个其反密码子刚好与 mRNA 互补的四叶草，，然后拿下其叶子上的氨基酸，用一个共价键将其粘到正在生成的蛋白质上。这种草的名字为转移 RNA（ tRNA）。

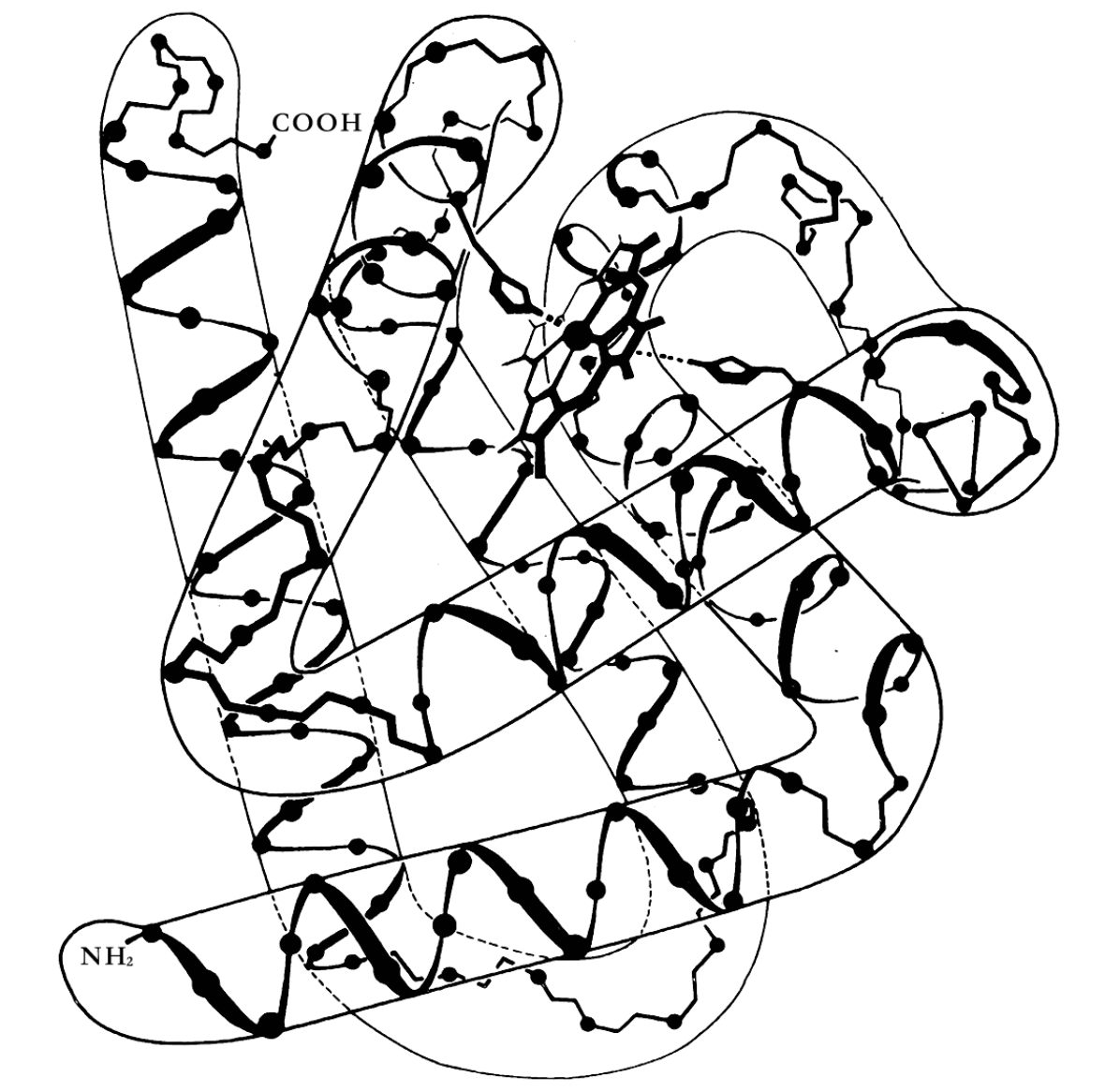
于是，简而言之，我们眼前是这样一幅画面:从 DNA 御座出发，DNA 把信使 RNA 的一些⻓串送到细胞 质中的核糖体上;而核糖体利用盘旋在自己周围的那些 tRNA“单词卡片”，根据 mRNA 中含有的蓝图，一个氨 基酸接一个氨基酸地、高效率地构造蛋白质。DNA 仅指示了蛋白质的一级结构。但这足够了，因为当蛋白质从 核糖体中出来时，它们便“魔术般地”折叠成复杂的形态，从而有能力像一台大功率的化学机器一样行动。

蛋白质功能

酶是如何在细胞里的分子上起作用？酶是折叠的多肽链，每个酶中都有一个裂缝或口袋或某种清晰定义的外观特性，酶在那里拴住某个种类的分子。这个地点叫活性部位，拴在那里的分子叫基质。酶可以有不止一个活性部位和不止一个基质。

一旦把酶与其基质拴在一起，就会发生某种电荷不平衡状态，随后，电荷——以电子或质子的形式——就围绕着拴住的分子流动并重新排布自己。达到平衡时，基质可能已经发生了意义深刻的化学变化。

丘奇—图灵论题

同构形式

假定有一种方法，一个有感知能力的生物可以利用它逐个把数分成两类。又假定这种方法总能在有穷的时间内得到答案，而且对于一个给定的数总能给出相同的答案。那么，存在某个有终止的 FlooP 程序（即一般的递归函数），它给出的答案恰好与这个有感知能力的生物的方法所得到的答案一样。而且，这个心智过程与这个 FlooP 程序在下述意义上同构：在某个层次上，计算机和大脑各自执行的那些步骤之间存在一个对应。

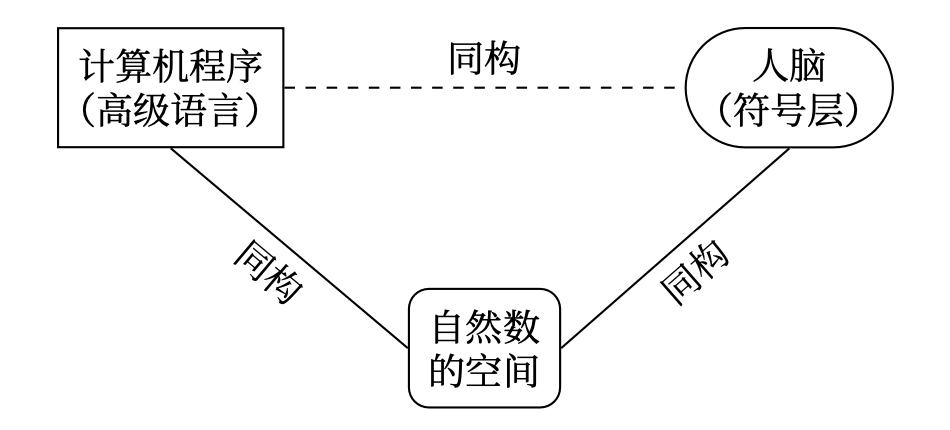
自然数的性质能在人类大脑和计算机程序中得到反映。这两个不同的描述因而能在一个适当的抽象层次上彼此对应

自然数的性质能在人类大脑和计算机程序中得到反映。这两个不同的描述因而能在一个适当的抽象层次上彼此对应

微观形式

一个生物体的各个组成部分的行为能用计算机来模拟。也就是说，任何元素（为典型起见，就假定是一个细胞）的行为，都能用一个 FlooP 程序（即一般递归函数）—— 在给定该元素的内部状态和外部环境的一个足够精确的描述之后 —— 计算到任意精确的程度。

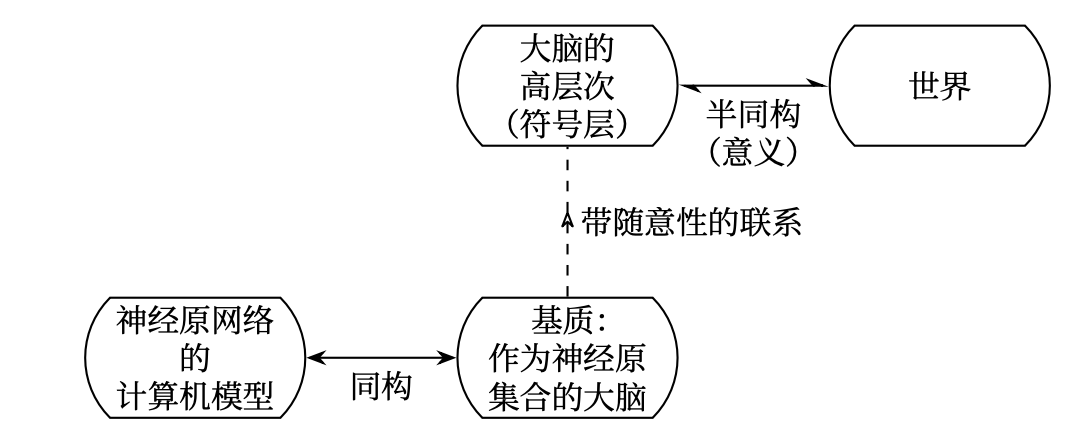
大脑的符号层漂浮于神经元活动之上，从而反应了世界。不过能在计算机上模拟的那种神经元活动本身并不能产生思维，那得靠组织中的一些更高的层次

大脑的符号层漂浮于神经元活动之上，从而反应了世界。不过能在计算机上模拟的那种神经元活动本身并不能产生思维，那得靠组织中的一些更高的层次

简化论形式

全部的大脑过程都可以从一个可计算的基质中导出。

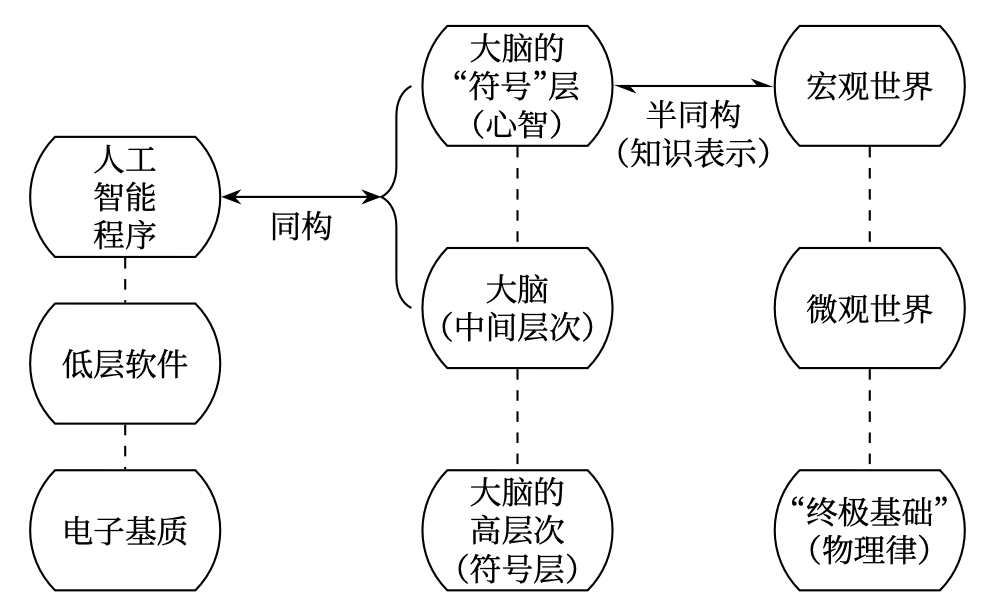
使人热衷于从事人工智能研究的关键，在于这样一种观念:心智的符号层次能从它们的神经原基质上被“撇出”，并用诸如 计算机的电子基质之类的方法实现。至于对大脑的复制需要做到什么深度，现在还完全不清楚

使人热衷于从事人工智能研究的关键，在于这样一种观念:心智的符号层次能从它们的神经原基质上被“撇出”，并用诸如 计算机的电子基质之类的方法实现。至于对大脑的复制需要做到什么深度，现在还完全不清楚

人工智能形式

任何种类的心智过程都可以用一个计算机程序来模拟，而该程序的基础语言与 FlooP 一样强，也就是说全体部分递归函数都能用这种语言程序化。

丘奇定理

在任何强如 TNT 的形式系统中都不可能有判定定理的过程。

人工智能

泰斯勒定理

一旦某些心智功能被程序化了，人们很快就不再把它看做“真正的思维”的一种本质成分。人工智能是尚未做到的东西。