碰撞及刚体动力学

碰撞检测系统（collision detection system）确保物体不会相互穿透，是任何游戏引擎的核心元件之一。而碰撞检测系统通常紧密地和物理引擎（physics engine）整合。当然，物理的范畴很广，在现游戏中所指的“物理”，更精确地说应该称为刚体动力学（rigid body dynamics）模拟。刚体（rigid body）是理想化，无限坚硬，不变形的固体物体。动力学（dynamics）是一个过程，计算刚体怎样在力（force）的影响下随时间移动及相互作用。

物理系统

以下是一些物理系统可以做的事情

• 检测动画物体和静态世界几何物体之间的碰撞。
• 模拟在引力及其他力影响下的自由刚体。
• 弹簧质点系统。
• 可破坏的建筑物和结构。
• 光线及形状的投射。
• 触发体积（判断物体进入/离开游戏世界中定义的区域，或逗留在那些区域的时间）。
• 容许角色拾起刚体。
• 复杂机器（起重机，移动平台谜题等）
• 陷阱（例如山崩和泥石）
• 带有逼真悬挂系统的可驾驶工具。
• 布娃娃式死亡。
• 富动力的布娃娃，真实地混合传统动画及布娃娃物理。
• 悬挂道具（水壶，项链，佩剑），半真实的头发/衣服移动。
• 布料模拟。
• 水面模拟及浮力。
• 声音传播。

物理对游戏的影响

对设计的影响

• 可预测性：若某事情必须每次都以某种方式发生，最好还是使用动画，而不需要逼动力学模拟确保每次产生相同的结果。
• 调校及控制：物理定律通常是不变的，调整物理参数的效果通常很不直观和很难可视化，要令一个角色向某个方向走，用调整力的方式比调整角色走路动画要难很多。
• 意外行为：有时候物理会产生游戏中预料之外的特征。

对工程的影响

• 工具管道：优良的碰撞/物理管道需要花长时间去建设和维护。
• 用户界面：玩家如何操控世界中的物理物体？能射击它们吗？能走进它们吗？能拾起它们吗？
• 碰撞检测：用于动力学模拟的碰撞模型，可能需要比非物理驱动的模型更细致，建模也需要更为谨慎。
• 人工智能：使用物理模拟的物体后，路径可能无法预测。
• 动画及动作角色：以动画驱动的物体可以轻微与另一个物体碰撞而不产生不良后果，但使用动力学模拟，物体可能会从另一个物体弹开，而且是以预料之外的形式，或产生严重的抖动。
• 布娃娃物理：布娃娃需要大量微调，而有时候会受模拟的不稳定所影响。
• 图形：物理驱动的动作或会影响可渲染物体的包围体积。
• 网络及多人：不影响游戏性的物理效果可以在客户端进行，影响的就需要在服务器上模拟，并将结果同步至客户端。
• 记录及重播：记录游戏过程及在稍后重播的能力，对除错/测试很有帮助，但也可以作为一个游戏功能。此功能在含有动力学模拟的游戏上更难实现，因为物理的混沌行为及物理更新的时间差异会导致重播结果与记录有所出入。

对美术的影响

• 额外的工具及工作流程复杂度：需要在物体中加入质量，摩擦力，约束，及其他动力学模拟的参数。
• 更复杂的内容：需要对一个物体建立多个不同用途的版本，每个版本含有不同的碰撞及动力学设置。
• 失控：物理驱动物体的不可预测性可能会令美术人员难以控制场景的艺术构图。

碰撞检测系统

碰撞检测系统的主要用途在于，判断游戏世界中的物体有否接触（contact）。

可碰撞实体

若希望游戏中某逻辑对象需要和其他对象碰撞，我们需要为该对象提供一个碰撞表达式（collision representation），以描述对象的形状及其在游戏世界的位置和定向。碰撞表达式是一个独特的数据结构，分离于对象的游戏性表达形式（gameplay representation）及视觉表达形式（visual representation）。

碰撞 / 物理世界

碰撞系统通常会通过一个名为碰撞世界（collision world）的数据结构，管理其所有的可碰撞实体。碰撞世界是专门为碰撞检测而设的游戏世界完整表达式。

若游戏含有刚体动力学系统，该系统通常会紧密地与碰撞系统整合。动力学系统的“世界”数据解结构通常会与碰撞系统共享，模拟中每个刚体通常会关联至碰撞系统里的一个可碰撞体。因此，碰撞世界有时候称为碰撞 / 物理世界，或直接称为物理世界（physics world）。

形状的概念

形状可以理解为一个由边界所指明的空间区域，能清楚界定形状的内外。有些游戏对象的类型，如地形，河流或者薄墙，最好以表面（surface）来表示。三维空间里，表面只有前后之分，没有内外之分。

相交

两集合的交集是它们共有成员所组成的集合。

接触

通常在游戏里我们没有兴趣追求严格意义上以点集表示的交集，我们只希望知道两个物体是否相交。碰撞事件发生的时候，碰撞系统通常会提供额外的关于接触性质的信息，里面一般会包含一个分离矢量（separating vector），我们可以把物体沿这个矢量移动，就能高效地把物体脱离碰撞状态。

凸性

在碰撞检测的范畴里，需要分辨凸（convex）和非凸（non-convex），或者是凹（concave）。

碰撞原型

碰撞检测系统一般只会支持有限的形状类型，有些碰撞系统称其为碰撞原型（collision primitive），因为这些形状可以作为基本组件构成更复杂的形状。

球体

球（sphere）体是最简单的三维体积。通过一个四元素浮点矢量表示。

胶囊体

胶囊体（capsule）是药丸形状的体积，由一个圆柱体加上两端的半球所组成。胶囊体由两点和半径表示。

轴对齐包围盒

轴对齐包围盒（axis-aligned bouding box，AABB）是一个矩形体积，六个面都与坐标系统的轴平行。AABB 可以用两个点定义，一个点是三个主轴上最小的坐标，另一个则是最大的坐标。

定向包围盒

若我们允许把轴对齐的盒子于其坐标系中旋转，便会得到定向包围盒（oriented bounding box，OBB）。OBB 通常会表示为 3 个半尺寸（半宽，半长，半高）再加上一个变换。

离散定向多泡型

离散定向多泡型（discrete oriented polytope，DOP）是比 AABB 和 OBB 更泛化的形状。DOP 是凸的泡型，用来逼近物体的形状。构建 DOP 的方法之一是，把多个置于无穷远的平面依其法矢量滑动，直至与所需逼近的物体接触。另一个方法是，构建 OBB，再把角或者边以 45° 切割，加入更多的平面视图做一个更紧密的逼近。

任意凸体积

多边形汤

有些碰撞系统也会支持完全任意，非凸的形状。这些形状通常是由三角形或其他简单多边形所构成。因此，这类形状通常称为多边形汤（polygon soup）。多边形汤常用于复杂的静态表面建模，如地形或建筑

碰撞测试及解释几何

碰撞系统应用到解释几何（analytical geometry）中三维体积及表面的数学描述，计算形状是否相交。

点与球体的相交

要判断点 \(\textbf{p}\) 是否在球体中，只需生成一个自球心至该点的分离矢量 \(\textbf{s}\)，然后量度该矢量的长度。若大于球体半径，则在球体之外，否则在球体之内。

\[ \textbf{s} = \textbf{c} - \textbf{p} \\ 若 |\textbf{s}| \leq r，则 \textbf{p} 位于球体内 \]

球体与球体的相交

生成链接两个球心的分离矢量 \(\textbf{s}\)，取其长度，与球的半径之和作比较。

\[ \textbf{s} = \textbf{c}_1 - \textbf{c}_2 \\ 若 |\textbf{s}| \leq (r_1 + r_2)，则两球体相交 \]

分离轴定理

多数碰撞检测系统都会大量使用分离轴定理（separating axis theorem）。此定理指出，若能找到一个轴，两个凸形状于该轴上的投影不重叠，就能确定两个形状不相交。若这样的轴不存在，并且那些形状是凸的，则可以确定两个形状相交。

要检测 A 和 B 两个形状是否相交，我们可以把这些形状逐一投影到各个潜在的分离轴，并检查两个投影区间 \([c^A_\text{min}, c^A_\text{max}]\) 和 \([c^B_\text{min}, c^B_\text{max}]\) 是否相交。数学上说，只有当 \(c^A_\text{max} < c^B_\text{min}\) 或 \(c^B_\text{max} < c^A_\text{min}\) 时，两个区间不相交。

AABB 与 AABB 的相交

使用分离轴定理即可，因为 AABB 与三个坐标轴平行，所以分离轴必定为某个坐标轴之一。逐个检测即可。

检测凸碰撞：GJK 算法

GJK 算法用于检测任意凸多胞形是否碰撞。

💡 闵可夫斯基差（Minkowski difference）：把 A 图形中的所有点，与 B 图形中的所有点成对相减，得出的集合 \(\{(\textbf{A}_i - \textbf{B}_j)\}\) 便是闵可夫斯基差。如果两个形状相交，其闵可夫斯基差会包含原点。

算法详情可以看这个 ppt。

GJK 算法可以处理所有凸形状之间的碰撞检测，而不同形状的唯一区别只在于算法所使用的的支持函数（support function）。

运动物体之间的碰撞

在游戏中，运动通常是以离散的时间步来模拟的，因此，简单的方法是在每个时间步中，将每个刚体的位置和定向当做是静止的，然后把静态相交测试施于这些碰撞世界的“快照”。然而，对于较小的高速移动物体，此方法将会失效。

细小快速的物体移动时，其路径可能会在碰撞世界的连续快照中留下空隙，这意味着可能会完全错过碰撞，此现象称为隧穿（tunneling）

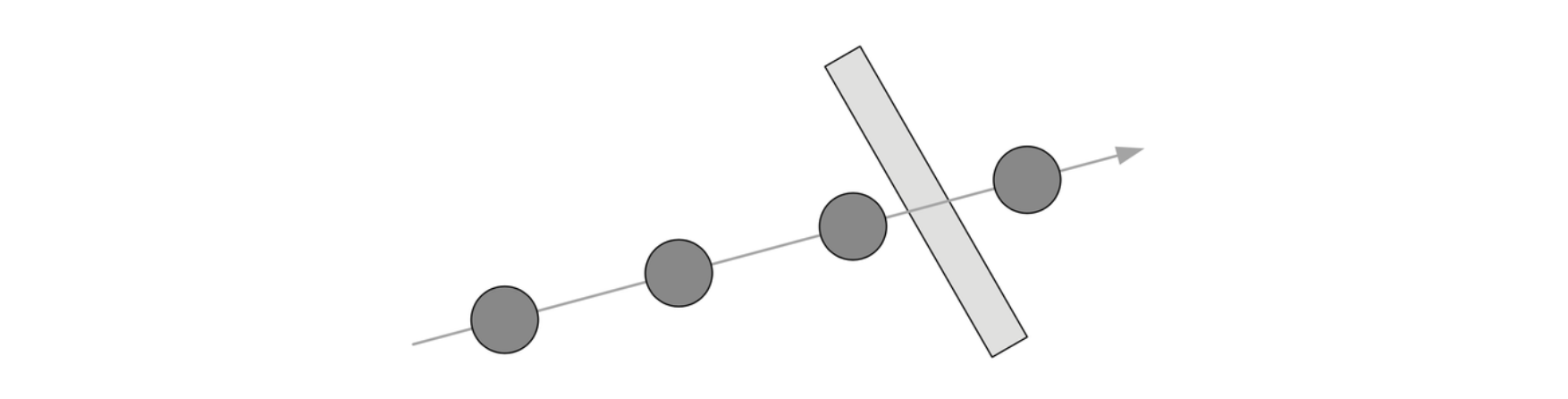
细小快速的物体移动时，其路径可能会在碰撞世界的连续快照中留下空隙，这意味着可能会完全错过碰撞，此现象称为隧穿（tunneling）

扫掠形状（swept shape）是一个形状随时间从某点移动至另一点所形成的形状。扫掠球体是胶囊体，扫掠三角形则是一个三角柱体。使用扫掠形状可以避免隧穿。检测相交的时候，使用测试形状从上一个快照的位置及定向移动至当前快照所形成的的扫掠形状。

💡 扫掠形状是有用的技术以确保碰撞不会在快照间错过，然而，若是沿着曲线路径进行线性插值，又或者涉及旋转的碰撞体，其测试结果一般是不准确的，所以可能要根据游戏所需使用更细密的技术。

性能优化

碰撞检测是 CPU 密集的工作，原因有二：

• 判断两个形状是否相交，所需的计算是非平凡的。
• 多数游戏含有大量的物体，随物体数量的递增，所需的相交测试会迅速增长。

时间一致性

时间一致性（temporal coherency）也称为帧间一致性（frame-to-frame coherency）。当碰撞物体以正常速率移动，在两时步中其位置及其定向通常会很接近，通过跨越多帧把结果缓存，我们可以避免每帧重新计算一些类型的信息。

空间划分

空间划分（space partitioning）的基本思路是将空间切割成较小的区域，以大幅降低需要做相交测试的碰撞体。例如八叉树，二元空间分割树，kd 树，球体树等。

阶段划分

Havok 采用三阶段的方式，缩减每时步中所需检测的碰撞体集合。

• 粗略阶段（broad phase）：用粗略的 AABB 测试判断哪些物体有机会碰撞。
• 中间阶段（midphase）：检测复合形状的逼近包围体。
• 精确阶段（narrow phase）：测试碰撞体中的个别碰撞原型是否相交。

碰撞查询

碰撞检测的另一个任务是回答有关游戏世界中碰撞体积的假想问题。

• 若从玩家武器的某个方向射出子弹，若能集中目标，那目标是什么？
• 汽车从 A 点移动到 B 点是否会碰到任何障碍物？
• 找出玩家在给定半径范围内的所有敌人对象。

这些操作称为碰撞查询（collision query）。

光线投射

回答以下问题

• 形状 A 能否“看到”形状 B？
• 形状 A 最先能看到什么形状 B？

光线投射（ray cast）通常以起点 \(\textbf{p}_0\) 以及增量矢量 \(\textbf{d}\) 来描述，起点加上增量矢量后会得到终点 \(\textbf{p}_1\)，此线段上的任何点都能在以下参数方程中求得

\[ \textbf{p}(t) = \textbf{p}_0 + t \textbf{d}, t \in [0, 1] \]

多数碰撞系统可以回传最早的接触，即最接近 \(\textbf{p}_0\) 的接触点。有些系统也会传回与光线相交的所有接触点的完整列表。

struct RayCastContact {
    F32 m_t; // 此接触点的 t 值
    U32 m_collidableId; // 击中哪个可碰撞体？
    Vector m_normal; // 接触点的法矢量
    // 其他信息
}

形状投射

回答以下问题

• 形状 A 沿一有向线段移动多远才能碰到其他物体？
• 判断虚拟摄像机是否和游戏世界中的物体碰撞。

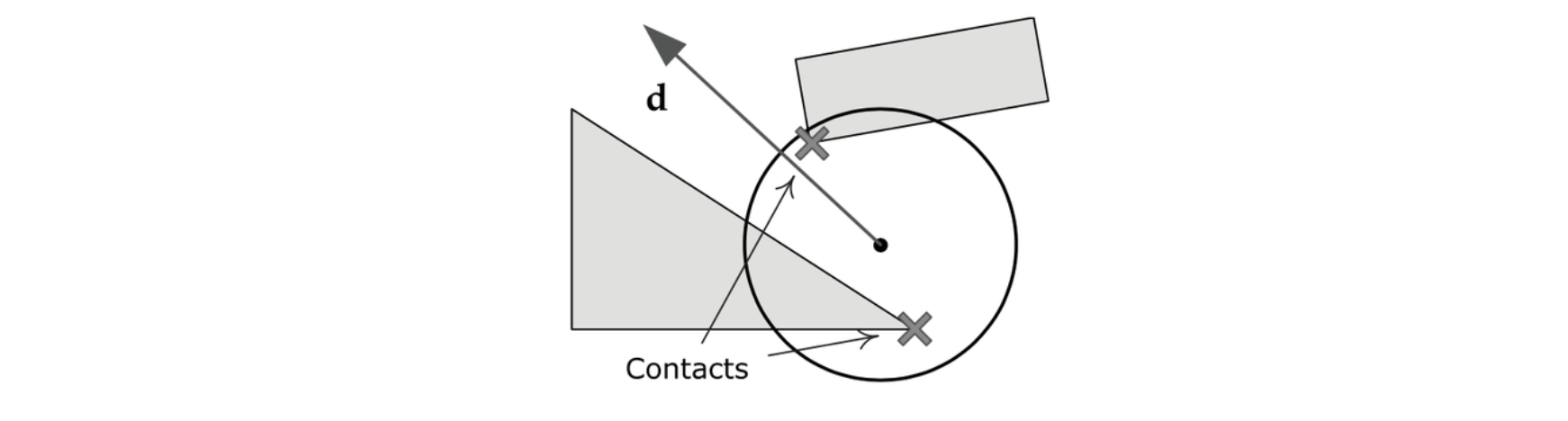
投射一个凸形状时有两个情况要考虑

• 投射形状已插入或接触到至少一个其他的碰撞体，因而阻止投射性状移动。
• 投射性状在起点没有与其他碰撞体相交，因此可以自由地沿路径移动一段非零距离。

球体在开始投射的时候已经穿透其他物体，无法移动

球体在开始投射的时候已经穿透其他物体，无法移动

球体还没有穿透其他物体，所以可以先沿着线段移动一段非零距离

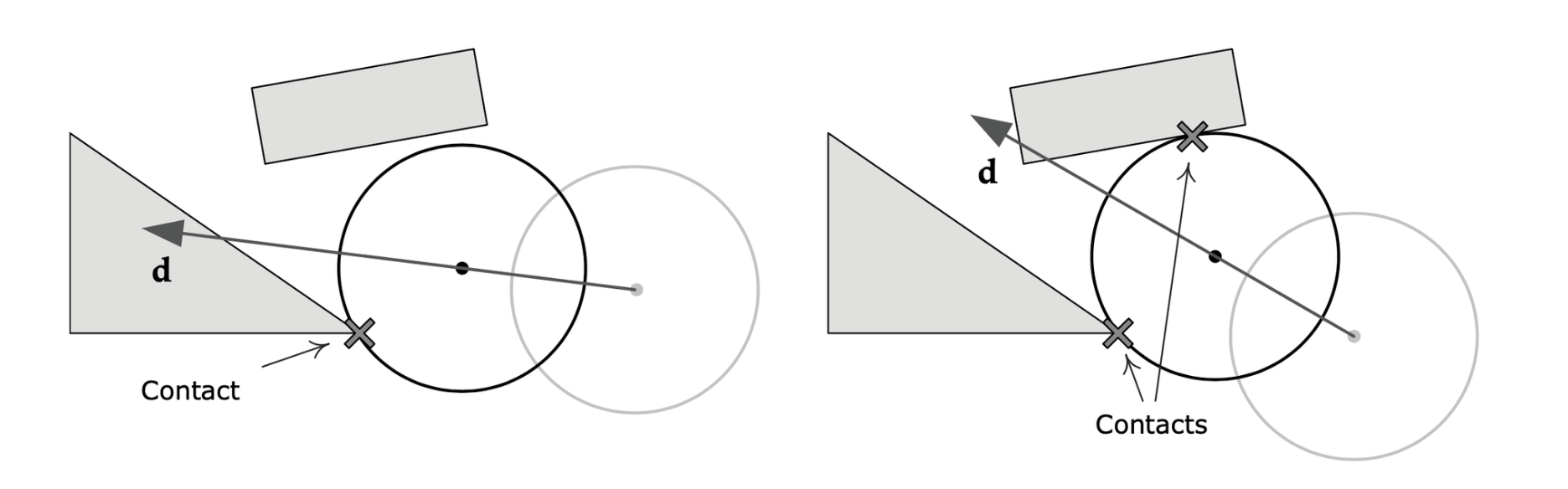
球体还没有穿透其他物体，所以可以先沿着线段移动一段非零距离

struct ShapeCastContact {
    F32 m_t; // 此接触点的 t 值
  U32 m_collidableId; // 击中哪个可碰撞体？
    Point m_contactPoint; // 实际接触点的位置
    Vector m_normal; // 接触点的法矢量
    // 其他信息
}

刚体动力学

一直以来，游戏中几乎只关注动力学中的经典刚体动力学（classical rigid body dynamics）。此术语意味着在游戏物理模拟中，做了两个重要的简化假设。

• 经典（牛顿）力学：假设物体服从牛顿运动定律，物体足够大，不会产生量子效应，物体的速度足够低，不会产生相对性效应。
• 刚体：模拟物体是完美的固体，不会变形。

基础

单位

多数刚体动力学模拟都会使用 MKS 单位系统。此系统中，距离以米（meter，m）量度，质量以千克（kilogram，kg）量度，时间以秒（second，s）量度。

分离线性及旋转动力学

无约束刚体（unconstrained rigid body），是指可以在 3 个笛卡尔轴上自由唯一，并绕这 3 个轴自由旋转的刚体。我们称这种刚体含 6 个自由度（degree of freedom，DOF）。

无约束刚体的运动可以分离为两个独立的部分。

• 线性动力学（linear dynamics）描述刚体旋转以外的运动。
• 旋转动力学（angular dynamics）描述刚体的旋转性运动。

质心

无约束刚体的行为有如把所有其物质集中于一个点，此点称为质心（center of mass，CM / COM）。质心本质是刚体在所有定向的平衡点。

\[ \textbf{r}_\text{CM} = \frac{\sum_{\forall i}m_i\textbf{r}_i}{\sum_{\forall i}m_i} = \frac{\sum_{\forall i}m_i\textbf{r}_i}{m} \]

对于凸刚体，质心位于刚体之内，凹刚体质心可能位于刚体之外。

线性动力学

线性速度和加速度

刚体的线性速度（linear velocity）定义了刚体质心的移动速度和方向。速度是位置对于时间的第一导数，可以写为

\[ \textbf{v}(t) = \frac{\text{d} \textbf{r}(t)}{\text{d}t} = \dot{\textbf{r}}(t) \]

线性加速度是线性速度对于时间的第一导数，又等于刚体质心位置对于时间的第二导数。

\[ \begin{align} \textbf{a}(t) &= \frac{\text{d} \textbf{v}(t)}{\text{d}t} = \dot{\textbf{v}}(t) \\ &= \frac{\text{d}^2\textbf{r}(t)}{\text{d} t^2} = \ddot{\textbf{r}}(t) \end{align} \]

力及动量

力（force）定义为任何能使含质量物体加速或减速的东西。力含模（magnitude）及空间中的方向，因为力都以矢量表示。

对刚体线性运动的净效应为那些力的矢量和

\[ \textbf{F}_\text{net} = \sum^N_{i=1} \textbf{F}_i \]

牛顿第二定律

\[ \textbf{F}(t) = m\textbf{a}(t) = m\ddot{\textbf{r}}(t) \]

当把刚体的线性速度和质量相乘，会得到线性动量（linear momentum）。

\[ \textbf{p}(t) = m\textbf{v}(t) \]

当质量不是常数的时候，下面的公式才是正确的牛顿第二定律

\[ \textbf{F}(t) = \frac{\text{d}\textbf{p}(t)}{\text{d}t} \]

运动方程求解

刚体动力学的中心问题是，给定一组施于刚体的已知力，对刚体的运动求解。

把力作为函数

力可以是刚体位置，速度或其他多个变量的函数，广义上可以表达为

\[ \textbf{F}(t, \textbf{r}(t), \dot{\textbf{r}}(t), \cdots) = m\ddot{\textbf{r}}(t) \]

常微分方程

广义来说，常微分方程（ordinary differential equation，ODE）是涉及一个自变量的函数及多个该函数导数的方程。若自变量是时间，而该函数是 \(x(t)\)，那么一个 ODE 是以下形式的关系

\[ \frac{\text{d}^n x}{\text{d}t^n} = f \Big( t, x(t), \frac{\text{d}x(t)}{\text{d}t}, \frac{\text{d}^2 x(t)}{\text{d}t^2}, \cdots, \frac{\text{d}^{n-1}x(t)}{\text{d}t^{n-1}} \Big) \]

所以广义上的力学方程可以写为

\[ \ddot{\textbf{r}(t)} = \frac{1}{m}\textbf{F}(t, \textbf{r}(t), \dot{\textbf{r}}(t)) \]

数值积分

游戏中几乎无法得出方程的解释解，所以通常使用数值积分（numerical integration）。使用这种技术，我们能对微分方程以时步（time step）的方式求解。

显式欧拉

对常微分方程最简单的数值求解方法之一是显式欧拉法（explicit Euler method）。假设在某一时刻我们得悉当前的速度，而我们希望对以下的常微分方程求解，以得到次帧的刚体位置：

\[ \textbf{v}(t) = \dot{\textbf{r}}(t) \]

使用显式欧拉法，我们只需要简单把速度乘以时间步，然后把一帧所移动的距离加到当前位置上，就得到物体在次帧的位置。

\[ \textbf{r}(t_2) = \textbf{r}(t_1) + \textbf{v}(t_1) \Delta t \]

类似的方法可以求次帧的速度

\[ \textbf{v}(t_2) = \textbf{v}(t_1) + \frac{\textbf{F}_\text{net}(t_1)}{m}\Delta t \]

韦尔莱积分

显式欧拉法常出现于游戏中的简单积分工作，当速度接近常数时它能产生最好的结果。然而，通用的动力学模拟并不会使用显式欧拉法，因为此法误差又高，稳定性又低。现在，游戏中常用的常微分方程数值方法大概是韦尔莱积分（Verlet integration）。韦尔莱积分有两个变种，正常韦尔莱和速度韦尔莱。

正常韦尔莱积分用往后的时间和往前的时间的泰勒级数求和得出。

\[ \begin{align*} \textbf{r}(t_1 + \Delta t) &= \textbf{r}(t_1) + \dot{\textbf{r}}\Delta t + \frac{1}{2}\ddot{\textbf{r}}(t_1) \Delta t^2 + \frac{1}{6}{\textbf{r}}^{'''}(t_1) \Delta t^3 + O(\Delta t^4) \\ \textbf{r}(t_1 - \Delta t) &= \textbf{r}(t_1) + \dot{\textbf{r}}\Delta t + \frac{1}{2}\ddot{\textbf{r}}(t_1) \Delta t^2 - \frac{1}{6}{\textbf{r}}^{'''}(t_1) \Delta t^3 + O(\Delta t^4) \end{align*} \]

两式相加消去相反的项可得正常的韦尔莱积分

\[ \textbf{r}(t_1 + \Delta t) = 2\textbf{r}(t_1) - \textbf{r}(t_1 - \Delta t) + \textbf{a}(t_1) \Delta t^2 + O(\Delta t^4) \]

用合力表示，则可以写成

\[ \textbf{r}(t_1 + \Delta t) = 2\textbf{r}(t_1) - \textbf{r}(t_1 - \Delta t) + \frac{\textbf{F}_\text{net}(t_1)}{m} \Delta t^2 + O(\Delta t^4) \]

速度韦尔莱用于计算经过一个时步的速度。

二维旋转动力学

二维中，每个刚体可当做一块材料薄片。所有线性运动在 xy 平面上发生，而所有旋转则是绕 z 轴发生。

角速度和加速度

角速度（angular velocity）实际上是标量，应该叫“角速率”，角速度以标量函数 \(\omega(t)\) 标记，单位是弧度每秒（rad/s）。角速率是定向角度 \(\theta(t)\) 对于时间的导数。

\[ \omega(t) = \frac{\text{d} \theta(t)}{\text{d}t} = \dot{\theta}(t) \]

角加速度（angular acceleration）是角速率的变化率。

\[ \alpha(t) = \frac{\text{d}\omega(t)}{\text{d}t} = \dot{\omega}(t) = \ddot{\theta}(t) \]

转动惯量

相当于质量，旋转动力学中有称为转动惯量（moment of inertia）的概念。就如质量代表改变点质量线性速度的难易程度一样，转动惯量是量度刚体在某轴上改变角速度的难易程度。

力矩

若某个力的施力线穿过刚体的质心，则该力仅产生线性运动，在其他情况下，该力除了产生线性运动，还会同时产生一个称为力矩（torque）的旋转力。

我们把施力的位置表示为矢量 \(\textbf{r}\)，此矢量是有质心延伸至施力点（也就是矢量 \(\textbf{r}\) 位于刚体空间，该空间的原点位于质心），由力 \(\textbf{F}\) 施于位置 \(\textbf{r}\) 所产生的力矩 \(\textbf{N}\) 为

\[ \textbf{N} = \textbf{r} \times \textbf{F} \]

当两个或以上的力施于一个刚体的时候，可以把各个力矩求和。最后需要关心的是净力矩 \(\textbf{N}_\text{net}\)。力矩对于角加速率和转动惯量，有如力对于线加速度和质量

\[ \textbf{N}_z = I\alpha(t) = I\dot{\omega}(t) = I\ddot{\theta}(t) \]

三维旋转动力学

刚体在三个坐标轴上的质量分布可以很不相同，不同轴的转动惯量会有所不同。在三维中，刚体的旋转质量由 \(3 \times 3\) 矩阵表示，此矩阵称为惯性张量（inertia tensor）。

\[ \textbf{I} = \begin{bmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{bmatrix} \]

此矩阵主对角线上的元素 \(I_{xx}, I_{yy}, I_{zz}\) 是刚体绕三个主轴的转动惯量。此矩阵的主对角线以外的元素称为惯量积（product of inertia）。

定向

三维中的刚体定向可以用一个 \(3 \times 3\) 的旋转矩阵 \(\textbf{R}\) 或者一个四元数 \(q\) 来表示。

角速度和角动量

三维中，角速度是一个矢量，可以看为以一个单位矢量 \(\textbf{u}\) 定义旋转轴，再乘以旋转平面上刚体的角速度标量 \(\omega_u = \dot{\theta}_u\)，因此

\[ \boldsymbol{\omega}(t) = \boldsymbol{\omega}_u(t)\textbf{u}(t) = \dot{\boldsymbol{\theta}}_u(t)\textbf{u}(t) \]

在无力矩情况下角速度矢量能改变的事实，说明角速度并不是守恒的，然而，另一个相关称为角动量（angular momentum）的量，在无力矩下仍维持不变，即角动量是守恒的。旋转动力学的角动量如同线性动力学的线性动量。

\[ \textbf{L}(t) = \textbf{I}\boldsymbol{\omega}(t) \]

碰撞响应

当刚体相互碰撞的时候，动力学模拟必须采取步骤确保它们对碰撞做出真实的响应，并且确保它们永不在模拟完成之后处于相互穿插的状态，此为碰撞响应（collision response）。

能量

当施力令刚体移动一段距离，称该力做了功（work）。功代表能量（energy）的改变。能量有两种形式：

• 刚体的势能（potential energy）\(V\)：仅仅来自其相对力场的位置而形成的能量。
• 刚体的动能（kinetic energy）\(T\)：代表该刚体相对于系统中其他刚体的能量。

由刚体形成的孤立系统，总能量 \(E = V + T\) 是守恒量。

线性运动形成的能量可以写成

\[ T_\text{linear} = \frac{1}{2}mv^2 = \frac{1}{2} \textbf{p}\cdot \textbf{v} \]

刚体旋转运动形成的动能为

\[ T_\text{angular} = \frac{1}{2} \textbf{L} \cdot \boldsymbol{\omega} \]

冲量碰撞响应

两个刚体在真实世界中碰撞，会产生一系列复杂的事件。刚体会被轻微压缩，然后反弹，改变其速度，并在过程中因为生成热和声音而损失一些能量。一个简化的定律称为无摩擦力下瞬时碰撞的牛顿恢复定律（Newton's law of restitution for instantaneous collisions with no friction），此定律用于简化碰撞假设。

• 碰撞的力作用于无穷短的时间内，这个力转化为理想化的冲量（impulse），这样令物体在碰撞的时候瞬间改变速度。
• 物体表面上的接触点无摩擦力。这意味着碰撞时分离物体的冲量垂直于这两个表面。
• 刚体间的复杂分子下互动，可以由单个简单的恢复系数逼近，习惯上标记为 \(\varepsilon\)。当 \(\varepsilon = 1\) 时，碰撞是完全弹性（perfectly elastic）的，没有任何能量损失，当 \(\varepsilon = 0\) 时，碰撞是完全塑性（perfectly plastic）的，一起失去两个刚体的动能。

所有碰撞基于动量守恒

\[ \textbf{p}_1 + \textbf{p}_2 = \textbf{p}_1' + \textbf{p}_2' \]

动能也是守恒的

\[ \frac{1}{2}m_1 v_1^2 + \frac{1}{2}m_2 v_2^2 = \frac{1}{2}m_1 v_1'^2 + \frac{1}{2}m_2 v_2'^2 + T_\text{lost} \]

其中能量损失为 \(T_\text{lost}\)，如果碰撞完全弹性，则 \(T_\text{lost}\) 为 0，否则带撇号的动能完全变为 0。

要使用牛顿恢复定律进行碰撞决议，我们在两个刚体上施加理想化的冲量。冲量标记为 \(\hat{\textbf{p}}\)，假设没有摩擦力，冲量矢量必然与接触点上垂直于两个表面，换言之，\(\hat{\textbf{p}} = \hat{p}\textbf{n}\)，其中 \(\textbf{n}\) 为垂直于两个表面的单位法矢量。两碰撞物体冲量方向相反，碰撞前后满足

\[ \begin{align} \textbf{p}_1' &= \textbf{p}_1 + \hat{\textbf{p}}, &~~~~~ \textbf{p}_2' &= \textbf{p}_2 - \hat{\textbf{p}} \\ m_1\textbf{v}_1' &= m_1\textbf{v}_1 + \hat{\textbf{p}}, &~~~~~ m_2\textbf{v}_2' &= m_2\textbf{v}_2 - \hat{\textbf{p}} \\ \textbf{v}_1' &= \textbf{v}_1 + \frac{\hat{p}}{m_1}\textbf{n}, &~~~~~ \textbf{v}_2' &= \textbf{v}_2 - \frac{\hat{p}}{m_2}\textbf{n} \end{align} \]

无摩擦力碰撞中，冲量作用于垂直于两表面接触点的直线，此直线以单位法矢量定义。

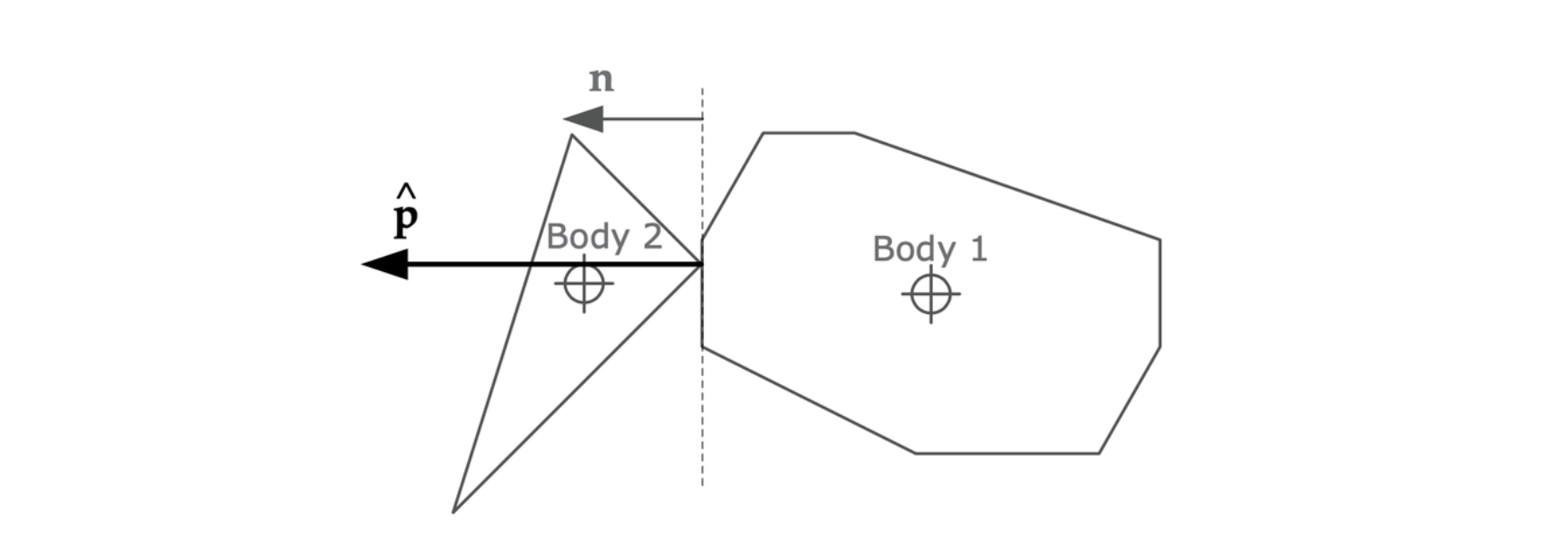
无摩擦力碰撞中，冲量作用于垂直于两表面接触点的直线，此直线以单位法矢量定义。

令两个刚体质心在碰撞前速度为 \(\textbf{v}_1, \textbf{v}_2\)，碰撞后速度为 \(\textbf{v}_1', \textbf{v}_2'\)，那么恢复系数 \(\varepsilon\) 定义为

\[ \textbf{v}_2' - \textbf{v}_1' = \varepsilon(\textbf{v}_2 - \textbf{v}_1) \]

对上述方程求解可得

\[ \hat{\textbf{p}} = \hat{p}\textbf{n} = \frac{(\varepsilon + 1)(\textbf{v}_2 \cdot \textbf{n} - \textbf{v}_1 \cdot \textbf{n})}{\cfrac{1}{m_1}+\cfrac{1}{m_2}} \]

休止，岛屿及休眠

当通过摩擦力，阻尼或其他方式削减模拟系统中的能量时，移动中的物体会最终停止。但在真实的计算中，多种因素会使得物体永远抖动不止，为了优化性能，多数物理引擎容许模拟中的动力学物体进入休眠（sleep）状态。这样可以令那些物体暂时撇除在模拟之外。

可使用多种条件判断刚体是否满足休眠的资格。

• 刚体受支持。刚体含有三个或者以上的接触点，能在引力或者其他施力下处于平冲状态。
• 刚体的线性及角动量低于预设阈值。
• 线性及角动量的移动平均低于预设阈值。
• 骨骼那题的总动能低于预设阈值。动能通常以质量归一化，从而可以不论质量大小把单个阈值用于所有物体。
• 对于将休眠的刚体，可以逐渐减慢其运动，令它能平滑地停止而不是突然停止。

约束

无约束的刚体有 6 个自由度，它能在三个维度上平移，并能绕三个笛卡尔轴旋转。约束（constraint）限制了物体的运动，削减了部分或完整的 DOF。

点对点约束

点对点（point-to-point constraint）是最简单的约束类型，它的作用如同球窝关节，刚体中某个指定的点与其他刚体的指定点对齐。

刚性弹簧

刚性弹簧约束（stiff spring constraint）很像点对点约束，区别是前者要保持两点分隔一段指定距离。

铰链约束

铰链约束（hinge constraint）限制旋转运动只能绕铰链旋转。无限制铰链（unlimited hinge）如同轮轴，容许物体旋转无限个圈。而有限制铰链（limited hinge）令物体只能在预设的角度内绕轴旋转。

滑移铰

滑移铰约束（prismatic constraint）的行为如活塞：受限的刚体运动只余一个平移自由度。滑移铰可选择容许或不容许刚体绕活塞的平移轴旋转。

布娃娃

布娃娃（ragdoll）是模拟人体在死亡或失去知觉时候的动作，即整个身体是瘫痪的。制作布娃娃的方法是，把一组刚体链接起来，每个刚体代表身体的半刚性部位。

控制刚体的运动

刚体除了要自然地受引力影响移动，响应对场景中其他物体的碰撞，多数游戏设计师还会要求对刚体有某种程度的控制能力。

引力

多数物理引擎会把引力加速度作为全局设置。

施力

游戏物理模拟中的刚体可施以任意数量的力，施力总是在有限的时间区间中进行的。游戏中的力一般是动态的，这些力可以在每帧改变其方向及绝对值。因此，多数物理引擎的施力函数会设计为每帧调用一次，而力的持续影响时间也是在该帧之内。

施力矩

当施力作用于刚体的质心，不会产生力矩，仅影响刚体的线性加速度。若力施于质心之外，就会同时产生线性及旋转加速度。此外，也能产生纯力矩（pure torque），方法是在离质心相同距离的对点上施以相反的等额的力。这对力所产生的线性运动会相互抵消，只留下旋转效果。这种产生力矩的一对力，称为力偶（couple）。

施以冲量

技术上来说，冲量是无穷短时间内的施力，然而，基于时间步的动力模拟中，最短的持续时间为 \(\Delta t\)，而这不够小去充分模拟冲量。所以，多数物理引擎会直接提供函数来对刚体施于冲量。

碰撞 / 物理步

每个碰撞 / 物理引擎都会在更新步时执行以下的基本工作。不同物理 SDK 可能会以不同的次序执行这些工作阶段。

1. 以 \(\Delta t\) 对施于物理世界刚体的力及力矩计算向前积分，求出次帧的暂定位置及定向。
2. 调用碰撞检测库，判断暂定移动是否有令物体间产生新的接触点。
3. 进行碰撞决议。常用的方法是使用冲量，惩罚性力，或作为以下约束求解的一部分。
4. 以约束求解程序满足约束条件。

💡 约束求解程序（constraint solver）本质上是一个迭代算法，尝试最小化刚体在物理空间的实际位置 / 定向与约束所定义的理想位置 / 定向的误差，以同时满足大量的约束。因此，约束求解程序本质上是迭代式误差最小化算法。

整合物理引擎至游戏

连接游戏对象和刚体

一般来说，游戏对象在碰撞 / 物理系统中会表示为零或多个刚体。

• 零个刚体：在物理世界中不含刚体的游戏对象适当做固体的，因为他们完全没任何碰撞表示方式。
• 一个刚体：大多数简单游戏对象只需要由单个刚体表示。
• 多个刚体：有些复杂游戏对象是由碰撞 / 物理世界中的多个刚体表示。比如 角色，机械，载具等。

物理驱动的刚体

若游戏中含有刚体动力学系统，那么有些对象会完全由模拟驱动。这些游戏对象称为物理驱动（physics-driven）对象。物理驱动刚体连接其游戏对象的方式，是通过步进模拟后，向物理系统查询刚体的位置和定向，之后，把这个变换施于整个游戏对象，或施于某个关节。

游戏驱动刚体

游戏世界的某些物体需要以非物理的方式移动，这种物体的运动可以由动画，样条路径或人类玩家所控制。我们通常希望这些物体参与碰撞检测，但不希望物理系统对这些物体有任何影响。为了支持这种物体，多数物理 SDK 提供一种特别的刚体类型，称为游戏驱动刚体（game-driven body）。

💡 要在物理世界中移动游戏驱动刚体，我们不能简单地在每帧设置其位置及定向，以配合对应游戏对象的位置。这样回产生不连贯性，令物理模拟非常难求解。因此，通常会使用冲量移动游戏驱动刚体。冲量即速度瞬时改变，以时间向前积分就能令刚体在时步末时到达所需的位置。

刚体固体

多数游戏世界是由静态几何物体和动态物体所组成的。为了模拟游戏世界的静态组件，多数物理 SDK 会提供一种特别的刚体，称为固定刚体（fixed body）。固定刚体的行为有如游戏驱动刚体，但固定刚体并不参与动力学模拟。

更新模拟

物理模拟需要定期更新，通常每帧一次。以下是完整的更新物理模拟所需的步骤。

• 更新游戏驱动刚体：更新物理世界中所有游戏驱动刚体的变换，令这些变换匹配其相连的游戏世界中的对象。
• 更新 phantom：每个 phantom 形状的行为，如同欠缺刚体的游戏驱动碰撞体。
• 施以力，冲量，并调整约束：更新游戏正在施行的力。本帧所发生的的游戏事件，其产生的冲量也在此施行。按需调整约束。
• 步进模拟：定期更新碰撞及物理引擎。包括
  • 对运动方程进行数值积分，求出所有刚体的次帧物理状态。
  • 执行碰撞检测算法，以求出物理世界中要求增加或删减的刚体接触。
  • 碰撞决议。
  • 施行约束。
• 更新物理驱动的游戏对象：从物理世界中获取物理驱动物体的变换，然后用这些变换更新相对的游戏对象或关节。
• phantom 查询：在物理步进之后，读取 phantom 形状的接触信息，做出游戏中的决定。
• 执行碰撞投射查询：已同步或异步的方式启动光线及形状投射。

单线程更新

非常简单的游戏循环如下所示。

F32 dt = 1.0f / 30.0f;

while (true) {
    g_hidManager->poll();

    g_gameObjectManager->**preAnimationUpdate**(dt);
    g_animationEngine->updateAnimations(dt);
    g_gameObjectManager->**postAnimationUpdate**(dt);
    **g_physicsWorld**->**step**(dt);
    g_animationEngine->pudateRagDolls(dt);
    g_gameObjectManager->**postPhysicsUpdate**(dt);
    g_animationEngine->finalize();

    g_effectManager->update(dt);
    g_audioEngine->update(dt);
    // ...
    g_renderManager->render();
    dt = calcDeltaTime();
}

• 游戏驱动刚体的位置通常于 preAnimationUpdate() 或 postAnimationUpdate() 中更新。
• 物理驱动刚体的位置通常在 postPhysicsUpdate() 中被读取。