动画系统

游戏会围绕一些角色进行——通常是人类或人性角色，有时候也会是动物或异形。引擎中的角色动画系统（character animation system）负责为角色灌输自然的动作。

角色动画的类型

赛璐璐动画

所有动画技术的前身是传统动画，或手绘动画。这种动画的动感由连续快速显示一串静止图片所产生，这些图片称为帧。赛璐璐动画（cel animation）是传统动画的一个种类。赛璐璐是透明的塑料片，上面可以绘画，把一连串含动画的赛璐璐放置在固定的手绘背景上，就能产生动感。

刚性层阶式动画

实现三维角色动画，最初的方法称为刚性层阶式动画（rigid hierarchical animation）。此方法中，角色由一堆刚性部分建模而成。

每顶点动画及变形目标

每顶点动画（per-vertex animation）由画师为网格的顶点添加动画，这些动作数据导出游戏引擎之后，就能告诉引擎在运行时如何移动顶点。但由于这是一项数据密集的技术，所以在实时游戏中很少会用到。

变形目标动画（morph target animation）虽然也是由画师移动网格的顶点，但是仅制作相对少量的固定姿势，运行时将姿势混合，并且将过度状态进行线性插值。

蒙皮动画

蒙皮动画（skinned animation）中，骨骼是由刚性的骨头构建而成的，这与刚性层阶动画一样，但是这些刚性的部件并不会显示，而是始终隐藏起来的。称为皮肤（skin）的圆滑三角形网格会绑定于骨骼上，其顶点会追踪关节（joint）移动。蒙皮上的每个顶点按照权重绑定多个关节，当关节移动的时候，蒙皮可以自然拉伸。

骨骼

骨骼（skeleton）由刚性的关节（joint）层阶结构所构成。由于骨骼是一个层级树状结构，所以可以通过关节树来表示。

struct Joint {
    Matrix4x3 m_invBindPose; // 绑定姿势的逆变换
    const char* m_name; // 人类可阅读的关节名字
    U8 m_iParent; // 父索引
}

struct Skeleton {
    U32 m_joinCount; // 关节数目
    Joint* m_aJoint; // 关节数组
}

姿势

把关节任意旋转，平移，甚至缩放，就能为骨骼摆出各种姿势。一个关节的姿势定义为关节相对参考系的位置，定向和缩放。骨骼的姿势仅仅是其所有关节的姿势集合。

绑定姿势

绑定姿势（bind pose）是指把网格当做正常，没有蒙皮，完全不涉及骨骼的三角形网格来渲染的姿势。又叫 T 姿势（T-pose），这是由于角色通常会站着，双腿稍微分开，双臂向左右伸直，形成 T 字形。

局部姿势

关节姿势最常见是相对于父关节指定的。相对父关节的姿势能令关节自然地移动。局部姿势（local pose）用于描述相对父的姿势，局部姿势存储为 SQT 格式（scale 缩放，quaternion 旋转以及 translation 平移）。

关节姿势就是一个仿射变换，第 j 个关节可以表示为 \(4 \times 4\) 仿射变换矩阵 \(\textbf{P}_j\)，此矩阵由一个平移矢量 \(\textbf{T}_j\)，\(3 \times 3\) 对角缩放矩阵 \(\textbf{S}_j\)，及 \(3 \times 3\) 旋转矩阵 \(\textbf{R}_j\) 所构成，整个骨骼的姿势 \(\textbf{P}^{skeleton}\) 可以写成所有姿势 \(\textbf{P}_j\) 的集合。

\[ \begin{align} \textbf{P}_j &= \begin{bmatrix} \textbf{S}_j \textbf{R}_j & \textbf{0} \\ \textbf{T}_j & 1 \end{bmatrix} \\ \textbf{P}^{skeleton} &= \{ \textbf{P}_j \} \mid ^{N-1}_{j = 0} \end{align} \]

💡 有些引擎不容许关节缩放，就会忽略 \(\textbf{S}_j\)，将其假定为单位矩阵。有些引擎会假设，如果用缩放，就使用统一缩放，即三个维度上缩放都相同。这样的好处是包围球不会变成椭球，也能减少存储空间。

关节姿势表示如下：

struct JointPose {
    Quaternion m_rot; // Q
    Vector3 m_trans; // T
    F32 m_scale; // S 为统一缩放
}

struct SkeletonPose {
  Skeleton* m_pSkeleton; // 骨骼 + 关节数量
    JoinPose* m_aLocalPose; // 多个局部关节姿势
}

全局姿势

把关节姿势表示为模型空间或世界空间会很方便。这称为全局姿势（global pose）。任何关节的全局姿势（关节至模型空间的变换）可以写成：

\[ \textbf{P}_{j \to M} = \prod^0_{i=j} \textbf{P}_{i \to \text{parent}(i)} \]

SkeletonPose 可以扩展为将全局姿势也存储在内。

struct SkeletonPose {
  Skeleton* m_pSkeleton; // 骨骼 + 关节数量
    JoinPose* m_aLocalPose; // 多个局部关节姿势
    Matrix44* m_aGlobalPose; // 多个全局关节姿势
}

动画片段

游戏是互动体验，玩家能全权控制角色，因此游戏的动画不可能是一串很长的连续的帧。取而代之，游戏角色的移动都必须拆分为大量小粒度的动作。我们称这些个别的动作为动画片段（animation clip），有时候简称动画。

局部时间线

每个动画片段各自有一条局部时间线（local timeline），该时间线通常使用自变量 \(t\) 表示。变量 \(t\) 的每个值称为时间索引。

动画师会在片段中指定的时间点上设置一些重要的姿势，这些姿势称为关键姿势（key pose）或关键帧（key frame），然后计算机会采用线性或基于曲线的插值计算中间的姿势。由于动画引擎能够对姿势插值，我们实际上能在片段间的任何时间采样，不一定要在整数帧索引上采样。所以动画片段的时间线是连续的。

全局时间线

正如每个动画片段都有一个局部时间线，游戏里的每个角色都有一个全局时间线。要把动画片段映射至全局时间线，需要以下的信息：

• 全局起始时间 \(\tau_{\text{start}}\)
• 其播放速率 \(R\)
• 其持续时间 \(T\)
• 循环次数 \(N\)

这样映射的方式如下，其中 \(t\) 为局部时间，\(\tau\) 为全局时间。

\[ \begin{align} t &= R(\tau - \tau_{\text{start}}) \\ \tau &= \tau_{\text{start}} + \frac{1}{R}t \end{align} \]

简单的动画数据格式

struct AnimationSample {
    JointPose* m_aJointPose; // 关节姿势数组
}

struct AnimationClip {
    Skeleton* m_pSkeleton;
    F32 m_framePerSecond;
    U32 m_frameCount;
    AnimationSample* m_aSamples; // 采样数组
    bool m_isLooping;
}

蒙皮及生成矩阵调色板

把三维网格顶点联系至骨骼的过程，称为蒙皮（skinning）。蒙皮用的网格是通过其顶点系上骨骼的，每个顶点可以绑定一个或多个关节。如果绑定一个关节，则其完全随关节移动，如果绑定至多个关节，则该顶点的位置就等于把它逐一绑至个别关节后的位置，再取加权平均。

蒙皮的结构如下：

struct SkinnedVertex {
    float m_position[3]; // (Px, Py, Pz)
    float m_normal[3]; // (Nx, Ny, Nz)
    float m_u, m_v; // 纹理坐标 (u, v)
    U8 m_jointIndx[4]; // 关节索引
    float m_jointWeight[3]; // 关节权重，略去最后一个
}

蒙皮矩阵

蒙皮网络的顶点会追随其绑定的关节而移动。蒙皮矩阵（skinning matrix）将网格顶点从原来的位置（绑定姿势）变换至骨骼的当前姿势。

令模型空间下标为 \(M\)，唯一关节的空间为 \(J\)，最初的绑定姿势为 \(B\)，当前姿势为 \(C\)。考虑一个蒙皮至这个关节的顶点，在绑定姿势时，该顶点的空间位置为 \(\textbf{V}^B_M\)，蒙皮过程要计算出该顶点在当前姿势的模型空间位置 \(\textbf{V}^C_M\)。

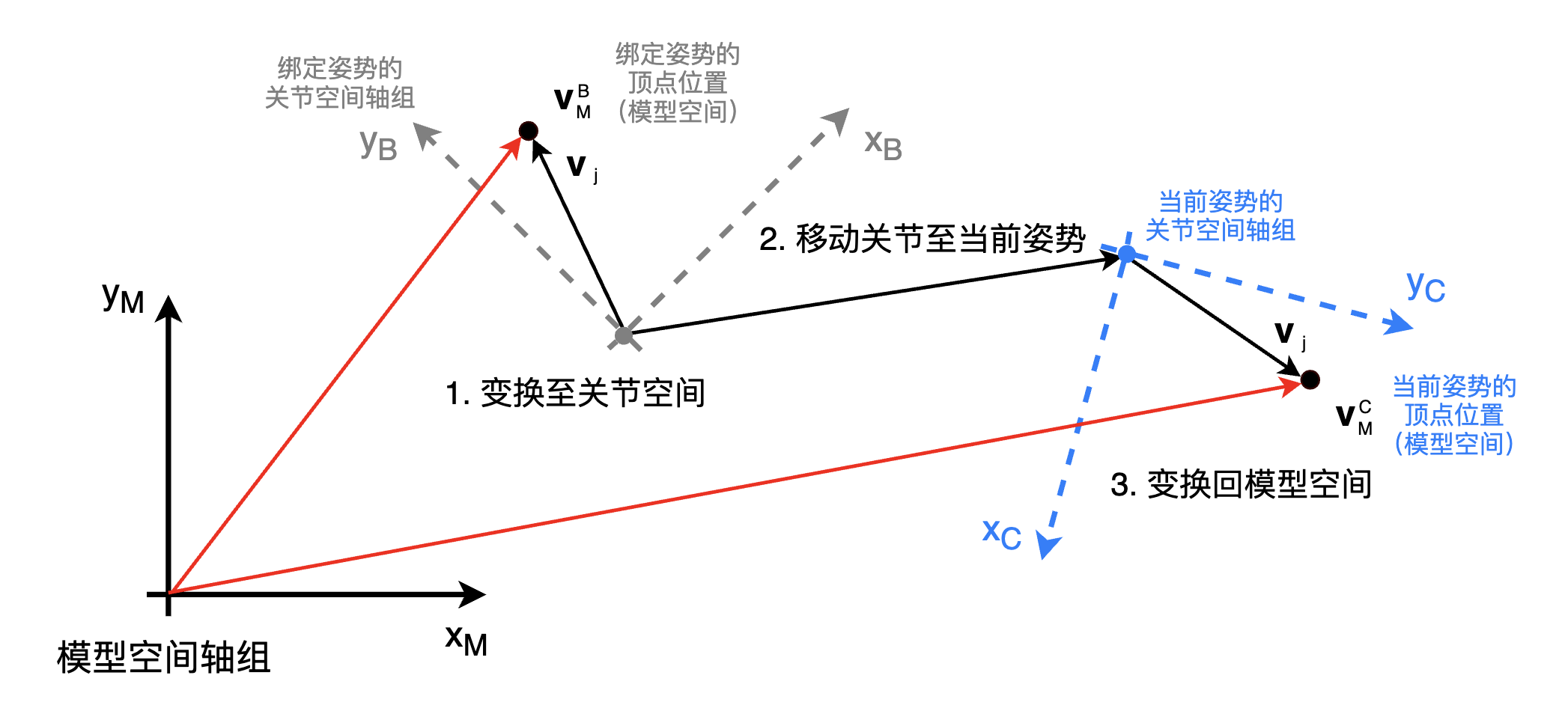
用矩阵 \(\textbf{B}_{j \to M}\) 表示关节在模型空间的绑定姿势。此矩阵把点或矢量从关节 \(j\) 的空间变换至模型空间。用 \(\textbf{C}_{j \to M}\)表示关节的当前姿势，吧顶点从绑定姿势变换为当前姿势的方程如下。

\[ \begin{align} \textbf{v}^C_M &= \textbf{v}_j \textbf{C}_{j \to M} \\ &= \textbf{v}^B_M(\textbf{B}_{j \to M})^{-1} \textbf{C}_{j \to M} \\ &= \textbf{v}^B_M \textbf{K}_j \end{align} \]

其中联合后的矩阵 \(\textbf{K}_j = (\textbf{B}_{j \to M})^{-1} \textbf{C}_{j \to M}\) 称为蒙皮矩阵。

矩阵调色板

我们要为每个关节 \(j\) 计算其蒙皮矩阵 \(\textbf{K}_j\)，此数组称为矩阵调色板（matrix palette）。当要渲染一个蒙皮网格时，矩阵调色板便要传送至渲染引擎。渲染引擎为每个顶点查找调试板中合适的关节蒙皮矩阵，并用该矩阵把顶点从绑定姿势变换至当前姿势。

💡 角色姿势随时间改变，其当前姿势矩阵 \(\textbf{C}_{j \to M}\) 就需要每帧更新。但绑定姿势是模型创建的时候确定下来的，所以 \((\textbf{B}_{j \to M})^{-1}\) 通常会缓存于骨骼。动画引擎会预先计算每个关节的局部姿势 \(\textbf{C}_{j \to p(j)}\)，然后再将这些矩阵转换至全局姿势 \(\textbf{C}_{j \to M}\)，最后把全局姿势乘以对应的绑定姿势逆矩阵，以生成每个关节的蒙皮矩阵 \(\textbf{K}_j\)。

当将一个顶点蒙皮至 \(N\) 个关节的时候，关节索引为 \(j_0\) 至 \(j_{N-1}\)，权重为 \(w_0\) 至 \(w_{N - 1}\)，则加权蒙皮矩阵的方程变为

\[ \begin{align} \textbf{v}^C_M &= \sum^{N - 1}_{i = 0} w_{ij}\textbf{v}^B_M \textbf{K}_{j_i} \end{align} \]

其中 \(\textbf{K}_{j_i}\) 是关节 \(j_i\) 的蒙皮矩阵。

动画混合

动画混合（animation blending）是指能令一个以上的动画片段对角色最终姿势起作用的技术。更准确地说，混合是把两个或更多的输入姿势结合，产生骨骼的输出姿势。

💡 混合作用结合两个或以上的动画，自动产生大量新动画。比如通过混合负伤的及无负伤 的步行动画，可以生成两者之间不同负伤程度的步行动画。

线性插值混合

给定两个骨骼姿势 \(\textbf{P}_A^{\text{skeleton}} = \{(\textbf{P}_A)_j\} |^{N - 1}_{j = 0}\) 及 \(\textbf{P}_B^{\text{skeleton}} = \{(\textbf{P}_B)_j\} |^{N - 1}_{j = 0}\)，我们希望求出此两极端的中间姿势 \(\textbf{P}_\text{LERP}^\text{skeleton}\)，可表达为

\[ \begin{align}(\textbf{P}_\text{LERP})_j &= \text{LERP}[(\textbf{P}_A)_j, (\textbf{P}_B)_j, \beta] \\ &= (1 - \beta)(\textbf{P}_A)_j + \beta(\textbf{P}_B)_j\end{align} \]

而整个骨骼的插值后姿势，仅仅是所有关节插值后姿势的集合：

\[ \textbf{P}_\text{LERP}^{\text{skeleton}} = \{(\textbf{P}_\text{LERP})_j\} |^{N - 1}_{j = 0} \]

💡 对两个骨骼姿势进行线性插值时，最自然的中间姿势通常是令关节独立在其父关节中间进行插值。换句话说，姿势混合通常在局部姿势进行。如果直接在模型空间混合全局姿势，其结果从生物力学上看显得不真实。

核心姿势

动画师通常会制定一组核心姿势（core pose），例如包括一个直立的核心姿势，一个蹲下姿势，一个躺下姿势等。只要确保角色的每个动画片段以某核心姿势开始，并以某核心姿势结束，就能简单把核心姿势匹配的片段链接成具 \(C^0\) 连续性动画。

时间性混合

给定两个于时间点 \(t_1\) 和 \(t_2\) 的姿势采样，一下方程可以求出位于此期间时间点 \(t\) 的姿势：

\[ \begin{align}\textbf{P}_j(t) &= \text{LERP}[\textbf{P}_j(t_1), \textbf{P}_j(t_2), \beta(t)] \\ &= (1 - \beta(t))\textbf{P}_j(t_1) + \beta(t)\textbf{P}_j(t_2)\end{align} \]

其中的混合因子 \(\beta(t)\) 为时间比率

\[ \beta(t) = \frac{t - t_1}{t_2 - t_1} \]

方向性运动

• 轴转移动（pivotal movement），因为转身的时候是以垂直轴进行旋转的。
• 靶向移动（targeted movement），使移动方向和面向方向相互独立的移动。

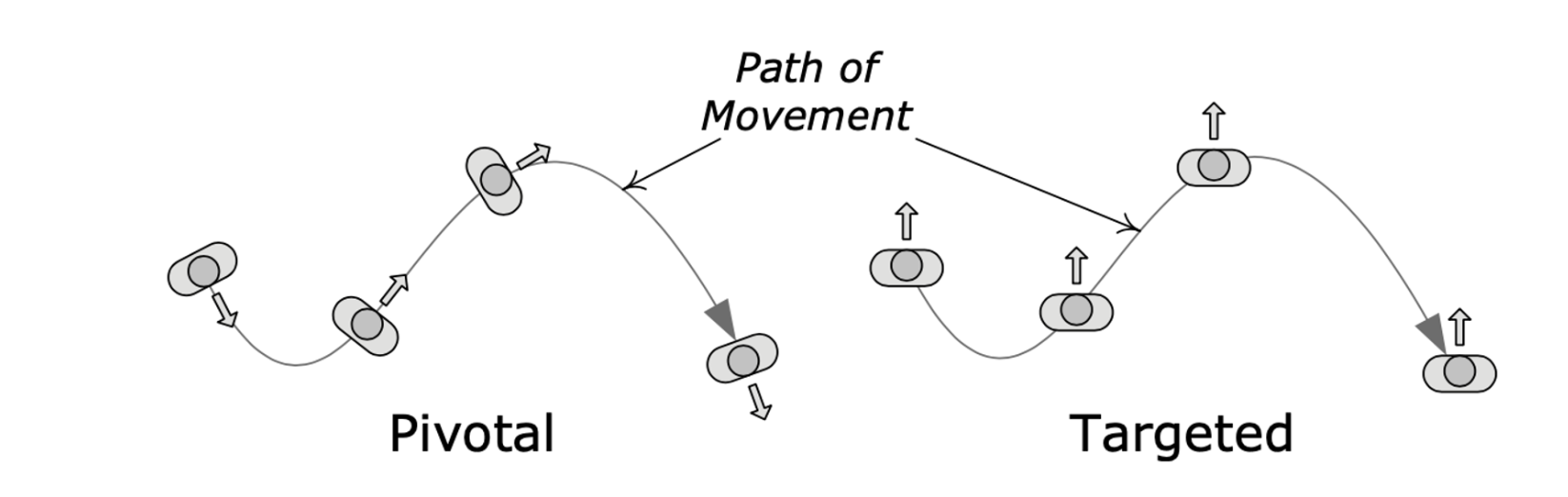
复杂的线性插值混合

一维线性插值混合

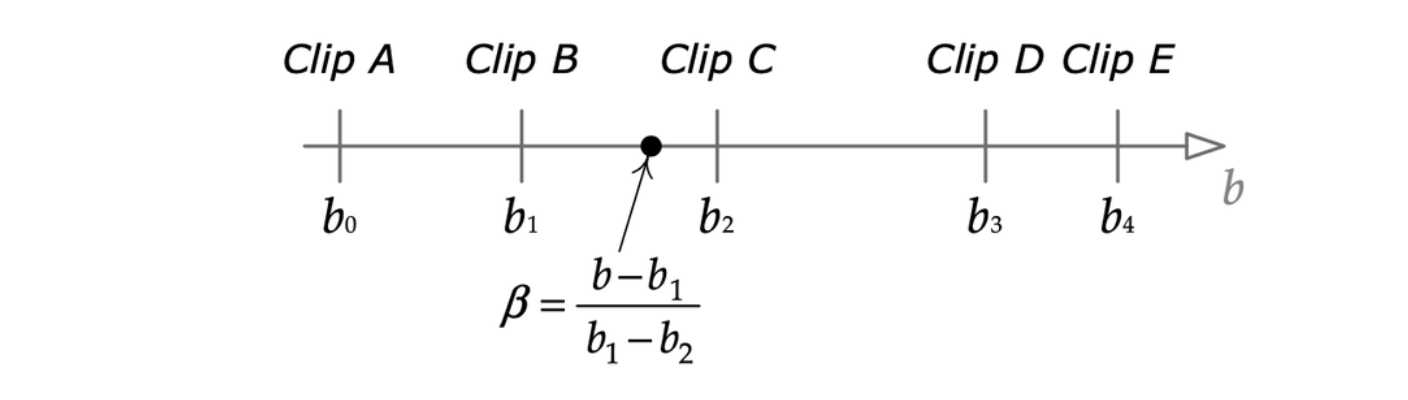
LERP 混合可以扩展至多于两个动画片段，此技术称为一维线性插值混合（one-dimensional LERP blending）。任意数量的片段至于一个范围内，给定任意的 \(b\) 值，选取两个最近于该值的片段，并用以下方程混合两者。

\[ \begin{align}\textbf{P}_j(t) &= \text{LERP}[\textbf{P}_j(t_1), \textbf{P}_j(t_2), \beta(t)] \\ &= (1 - \beta(t))\textbf{P}_j(t_1) + \beta(t)\textbf{P}_j(t_2)\end{align} \]

其中 \(\beta\) 为

\[ \beta = \frac{b - b_i}{b_{i+1} - b_i}, b \in [b_i, b_{i+1}] \]

靶向移动可以看成是特殊的一维线性插值混合。

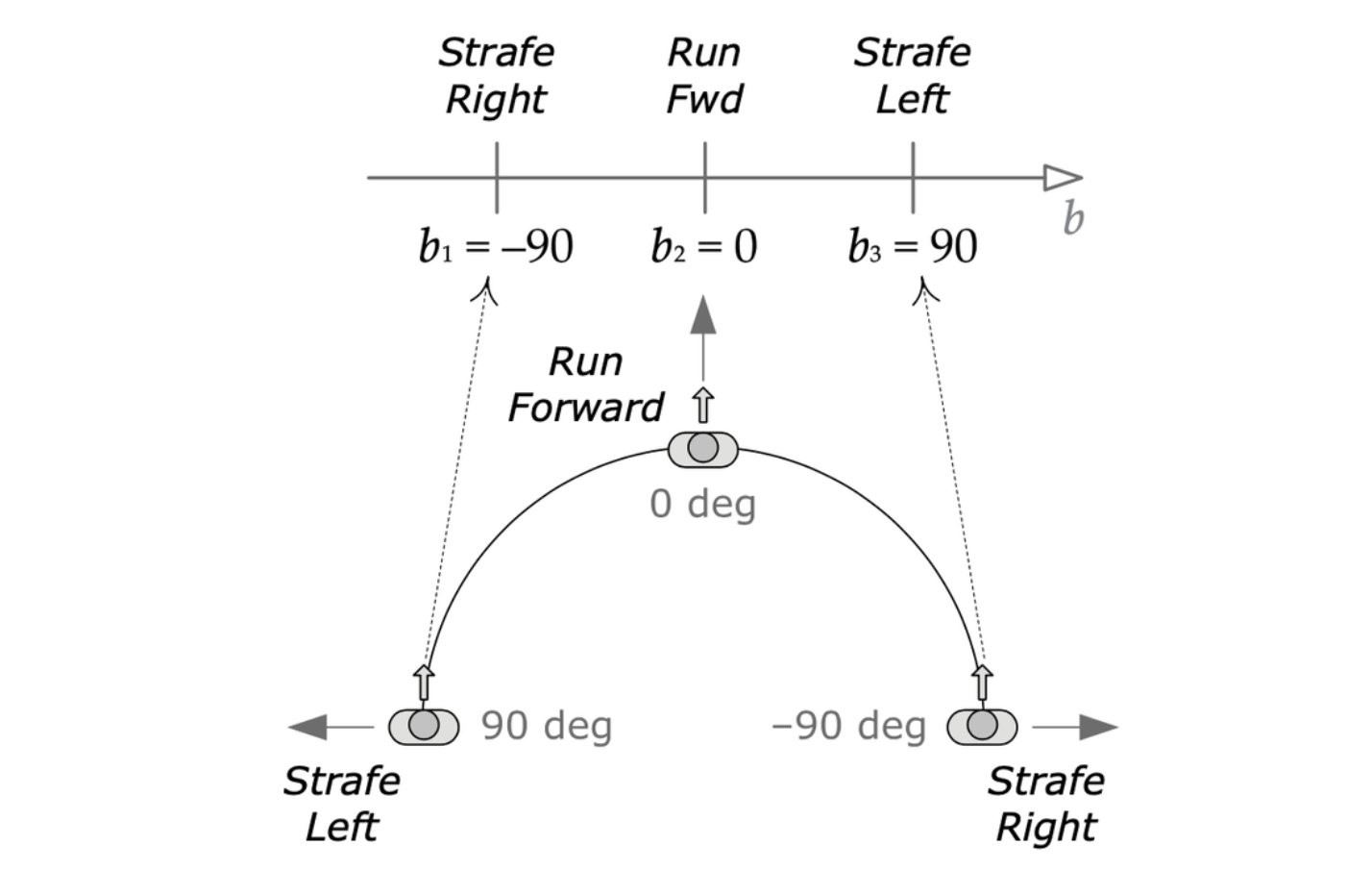
二维线性插值混合

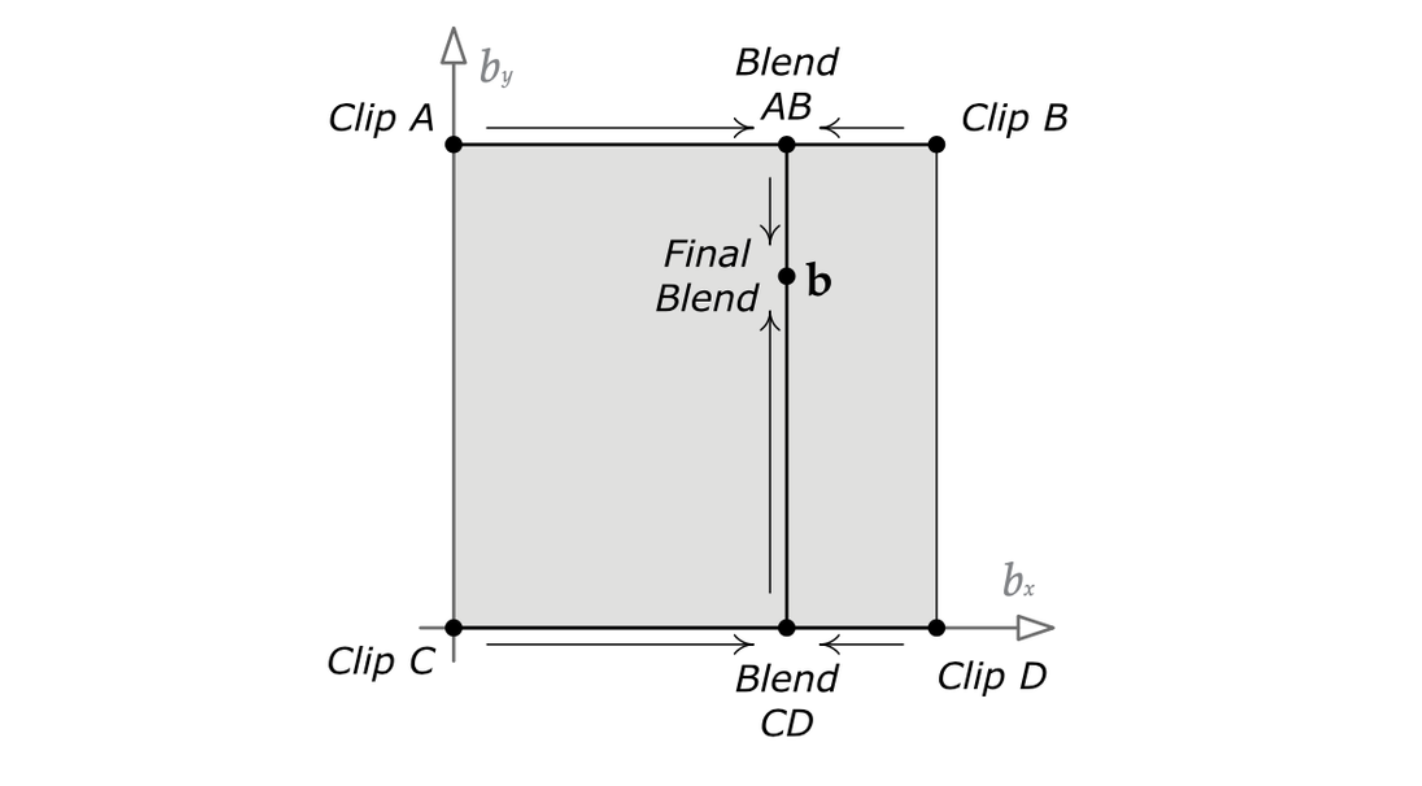
有时候我们想圆滑地同时改变角色动作的两个方面。例如我希望角色能用武器在水平及垂直方向瞄准。二维混合致涉及 4 个动画片段，这些片段位于正方形的四角。

• 利用水平混合因子 \(b_x\) 求出两个中间姿势，一个在顶边两个动画片段中间，一个在底边两个片段中间。这两个姿势用简单的一维 LERP 混合求得。
• 再使用垂直混合因子 \(b_y\)，把两个中间姿势用一维 LERP 混合求出最终姿势。

骨骼分部混合

人可以独立控制身体的不同部位。实现这种动作的方法之一是，骨骼分部混合（partial-skeleton blending）技术。骨骼分部混合在每关节设置不同的混合百分比，对每个关节 \(j\) 定义一个独立的混合百分比 \(\beta_j\)。整个骨骼的混合百分比集合 \(\{\beta_j\} |^{N-1}_{j=0}\) 有时候称为混合遮罩（blend mask），因为这可以把某些关节混合百分比设置为 0，来掩盖那些关节。

加法混合

加法混合（additive blending）引入一种称为区别片段（difference clip）的新类型动画。区别动画代表两段正常动画的区别，将其加进普通的动画片段，可以产生一些有趣的姿势和动作变化。

给定骨骼中每个关节 \(j\) 的来源姿势 \(\textbf{S}_j\) 和参考姿势 \(\textbf{R}_j\)，区别姿势 \(\textbf{D}_j\) 可定义如下

\[ \textbf{D}_j = \textbf{S}_j \textbf{R}_j^{-1} \]

把区别姿势 \(\textbf{D}_j\) “加进”目标姿势 \(\textbf{T}_j\) 会产生新的加法姿势 \(\textbf{A}_j\)。

\[ \textbf{A}_j = \textbf{D}_j \textbf{T}_j = (\textbf{S}_j \textbf{R}_j^{-1}) \textbf{T}_j \]

移动噪声

人在跑步的时候动作不尽相同，肯定会有所变化。加法混合可用于在完全重复的移动周期上叠加上随机性，反应和分心的表现。

后期处理

一旦一个或多个动画片段生成骨骼的姿势，然后通过线性插值或加法混合把结果混合成一个姿势，在渲染角色之前，通常还要再修改姿势，此修改称为动画后期处理（animation post-processing）。

程序式动画

程序式动画（procedural animation）是指任何在运行时生成的动画，这些动画并非由动画工具导出的数据所驱动的。

逆运动学

正向运动学（forward kinematics）的输入是一组局部姿势，输出是一个全局姿势，以及每关节的蒙皮矩阵。逆运动学（inverse kinematics）输入是某关节想要的全局姿势，此输入称为末端受动器（end effector），要求输出其他关节的局部姿势，是末端受动器能达到指定的位置。

动画架构系统

多数动画系统由 3 个分明的软件层组成。

• 动画管道（animation pipeline）
  • 对于游戏中每个含动画的角色及物体，动画管道为它们取得一个或多个动画片段及对应的混合因子作为输入，把这些片段混合后产生一个局部骨骼姿势作为输出。
  • 为骨骼计算一个全局姿势，以及生成蒙皮矩阵调色板供渲染引擎使用。
  • 为后期处理提供钩子，以便生成全局姿势及蒙版矩阵前可以修改局部姿势。
• 动作状态机（ASM，action state machine）
  • ASM 位于动画管道之上，并提供以状态驱动的动画接口供所有高层游戏代码之用。
  • ASM 确保角色从一个状态圆滑地过渡到另一个状态。
• 动画控制器（animation controller）
  • 每个控制器是特别为管理某个角色行为模式而设置的。

动画管道

此管道的各个阶段如下

• 片段解压及姿势提取：在此阶段中，每个片段的数据会被压缩，并提取所需时间索引的静态姿势。此阶段的输出是每个输入片段一个局部骨骼姿势。
• 姿势混合：通过全身 LERP 混合，分部 LERP 混合，或加法混合，把输入姿势结合在一起。本阶段的输出是一个对应骨骼中所有关节的局部姿势。
• 全局姿势生成：遍历骨骼层次结构，把局部关节串接以产生骨骼的全局姿势。
• 后期处理（可选）：输出最终姿势之前，有机会修改骨骼的局部及全局姿势。
• 重新计算全局姿势：许多种类的后期处理都需要全局姿势作为输入，但却只生成局部姿势作为输出，当执行了这种后期处理步骤，我们必须从修改后的局部姿势重新计算全局姿势。
• 矩阵调色板生成：把每个关节的全局姿势矩阵乘以对应的逆绑定姿势矩阵。本阶段的输出为渲染引擎所用的蒙皮矩阵调色板。

典型的动画管道

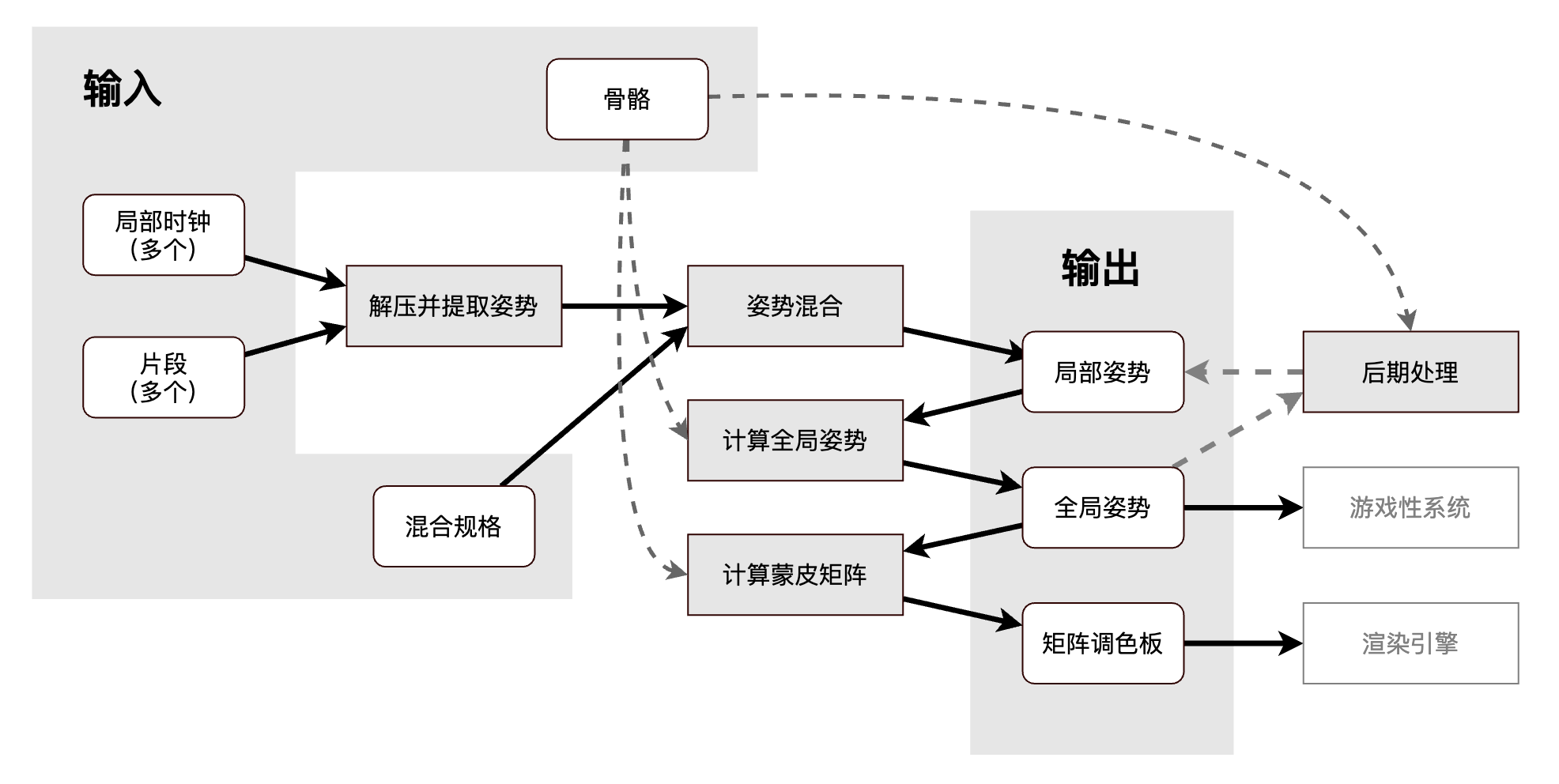
典型的动画管道

数据结构

共享数据资源

• 骨骼：描述关节层次结构及其绑定姿势。
• 蒙皮网格：一个或多个可蒙皮至单个骨骼的网格。
• 动画片段：为每个角色骨骼制作的数百甚至数千个动画片段。

共享动画资源的 UML 图

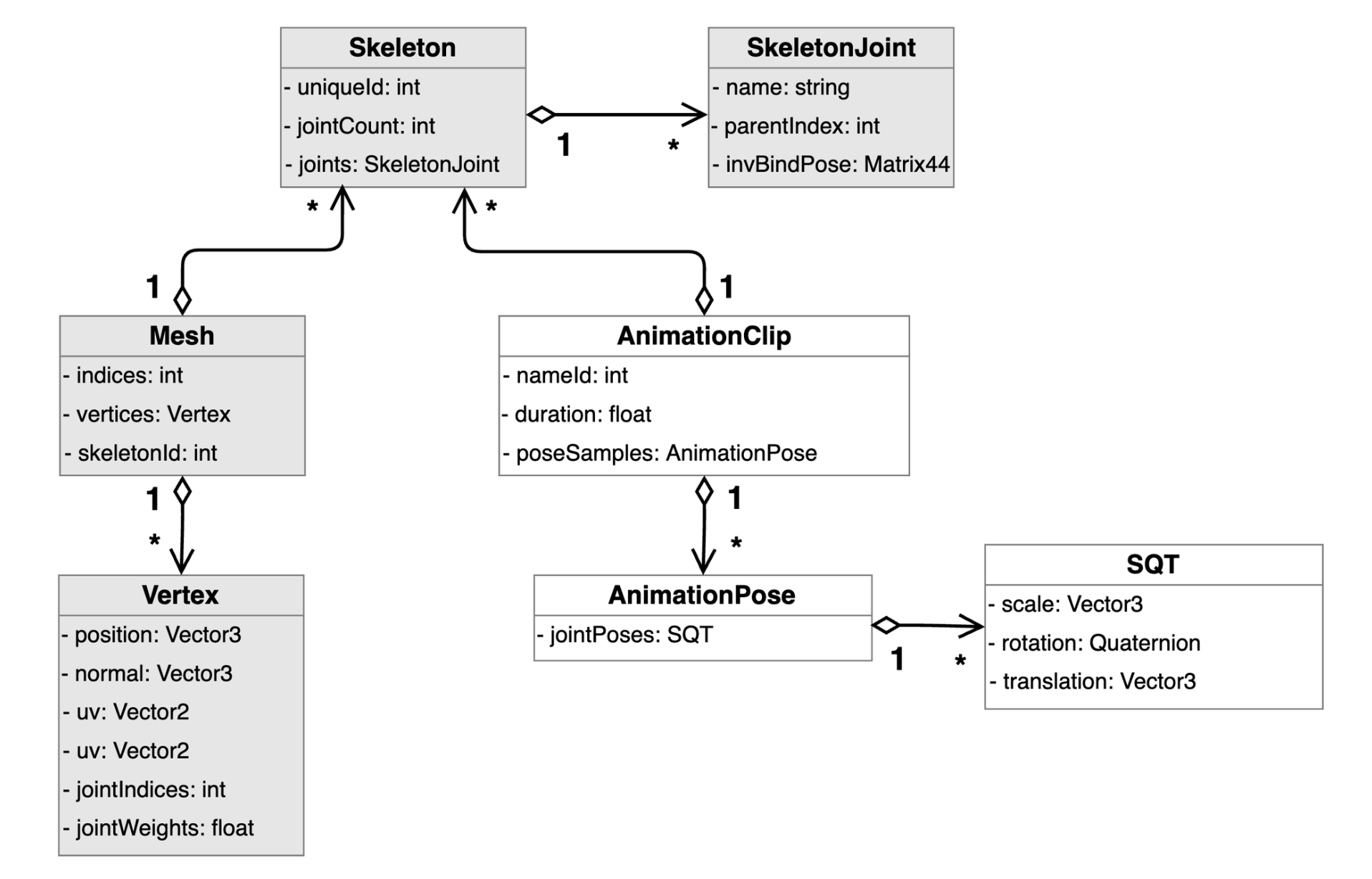
共享动画资源的 UML 图

实例数据

• 片段状态：每个播放片段包含局部时钟和播放速率。
• 混合规格：描述哪些动画片段正在播放，以及这些片段如何混合在一起。
• 分部骨骼关节权重：每个节点对最终姿势的影响力会存储为一组关节权重。
• 局部姿势：一个 SQT 数组的数据结构，每个 SQT 对应于一个关节，存储成相对于父关节的骨骼最终姿势。
• 全局姿势：每个元素对应于一个关节，存储模型空间或者世界空间的最终骨骼姿势。
• 矩阵调色板：每个元素对应于一个关节，存储蒙皮矩阵，供渲染引擎之用。

动作状态机

在底层管道和游戏角色/其他动画系统客户端之间，通常会引入一个软件层。此软件层会实现为状态机，称为动作状态机（action state machine）或动画状态机（animation state machine）。

动画状态

动画师，游戏设计师和程序员通常会一起合作创造游戏里中心角色的动画及控制系统。这些开发者需要一种方式描述角色 ASM 的状态，编排每个混合树结构，并在混合树种选择片段做输入。

只需要四种原子混合节点类型就能构建任意复杂的混合树。分别为：

• 片段
• 二元 LERP 混合
• 二元加法混合
• 三元 LERP 混合

下面是一个 Scheme 的状态描述例子

(define-state simple
    :name "pirate-b-bump-back"
    :clip "pirate-b-bump-back"
    :flags (anim-state-flag no-adjst-to-ground)
)

(define-state complex
    :name "move-l-to-r:
    :tree
        (anim-node-lerp
            (anim-node-clip "walk-l-to-r")
            (anim-node-clip "run-l-to-r")
        )
)

过渡

为了制作高质量的角色动画，我们必须小心处理动作状态机中的状态过渡，以确保动画链接之处不会出现突兀或粗糙的感觉。

除非来源状态的最终姿势和目标状态的初始姿势完全一致，否则需要过渡来将状态从来源状态跳到目标状态。淡入和淡出是一个选项，但是有时候也需要在状态机中引入特殊的过渡状态来达到目的。

过渡的参数可以为下面列出的

• 来源及目标状态
• 过渡类型
• 持续时间
• 淡入淡出的曲线类型
• 过渡窗口（某些过渡只有在来源动画的局部时间位于某个窗口内才能进行）

过渡矩阵

过渡矩阵表明所有状态之间的过渡。