渲染引擎
三角形光栅化基础
三维场景渲染的本质涉及以下几个基本步骤。
- 描述一个虚拟场景(virtual scene),这些场景一般是易某数学形式表示的三维表面。
- 定位及定向一个虚拟摄像机(virtual camera),为场景取景。摄像机位于一个理想化焦点,在焦点前的近处悬浮这一个影像面。
- 设置光源(light source),光源产生的光线会与环境中的物体交互作用并反射,最终到达虚拟摄像机的感光像面。
- 描述场景物体表面的视觉特性(visual property),这些视觉特性决定光线如何与物体表面产生交互作用。
- 对每个位于影像矩形内的像素,渲染引擎会找出经过该像素而聚焦于虚拟摄像机焦点的光线,并计算其颜色和强度,此过程称为求解渲染方程(solving the rendering equation),也叫着色方程(shading equation)。
几乎所有三维计算机图形技术,在高层次来看都会使用这种渲染方法
实时渲染引擎重复地进行上述的步骤,以每秒 30、50 或 60 帧的速度显示渲染出来的影响,从而产生运动的错觉。
场景描述
场景有物体组成,所有物体都占据三维体积。物体可以分为
- 不透明的(opaque):光不能通过物体。
- 透明的(transparent):光能通过该物体,过程中不被散射。
- 半透明的(translucent):光能通过该物体,但过程中会被散射到各个方向。
渲染不透明物体的时候,只需考虑其表面,对于不透明物体的渲染,如果精细的话需要知道其物理特性并为其建模,不过一般引擎不会这么复杂,只会使用 alpha 这种简单的不透明度数值来模拟。所以可以说,大部分游戏渲染引擎,只会着重于渲染物体的表面。
三角形网格
用三角形网格的原因在于
- 三角形是最简单的多边形。
- 三角形必然是平坦的。
- 三角形经过多种变换后仍然维持是三角形,这对于仿射转换和透视转换也成立。
- 几乎所有商用图形加速硬件都是为了三角形光栅化而设计的。
三角形由三个定点矢量 \(\textbf{p}_1, \textbf{p}_2, \textbf{p}_3\) 构成,每条棱为
\[ \begin{align} \textbf{e}_{12} &= \textbf{p}_2 - \textbf{p}_1 \\ \textbf{e}_{13} &= \textbf{p}_3 - \textbf{p}_1 \\ \textbf{e}_{23} &= \textbf{p}_3 - \textbf{p}_2 \\ \end{align} \]
其面法线(face normal)为
\[ \textbf{N} = \frac{\textbf{e}_{12} \times \textbf{e}_{13}}{|\textbf{e}_{12} \times \textbf{e}_{13}|} \]
索引化三角形表(indexed triangle list)用于表示三维网格,三角形定点只列举一次,存在于顶点数组(vertex array)中。然后三角形则用索引来引用这些定点,存于索引数组(index array)。缓存还能通过三角形带(triangle strip)和三角形扇(triangle fan)来进行优化,这两种方式不需要索引数组,而是直接根据定点顺序来理解三角形。
镶嵌(tessellation)
镶嵌是指把表面分割为一组离散多边形的过程,这些多边形通常是三角形或四边形。三角化(triangulation)专指吧表面镶嵌为三角形。
层次细节(LOD,level of detail)
游戏开发者经常以一串不同版本的三角形网络链去逼近理想的三角形对像素的密度,每一个版本称为层次细节(LOD,level-of-detail)。当物体远离计算机,引擎会把网络换成更低级别的细节,这样渲染引擎就能将更多的时间用在接近摄像机的物体上。
渐进网络(progressive mesh)
当物体很接近摄像机时采用单个最高分辨率网格,当物体自摄像机远离时,这个网格会自动密铺,将某些棱收缩为点。此过程能自动生成半自动的 LOD 链。
模型空间
三角形网格的位置矢量,会被指定于一个便利的局部坐标系,此坐标系可称为模型空间。模型空间的原点一般不是物体中心,而是一个便利的位置,比如角色脚掌所在地板的位置,车辆轮子在地上的水平质心。
每个网格可以在场景中多次出现,比如成排的路灯,桌子椅子等,这称为网格的实例化。每个这些物体称为网格的实例(mesh instance)。每个网格包含一个共享网格的引用,也包含一个变换矩阵,此矩阵为模型至世界矩阵,或简称为世界矩阵(world matrix)。此矩阵为
\[ \textbf{M}_{M \to W} = \begin{bmatrix} (\textbf{RS}_{M \to W} & \textbf{0}) \\ \textbf{t}_M & 1 \end{bmatrix} \]
其中左上角的 \(\textbf{RS}_{M \to W}\)用于旋转和缩放模型空间的顶点至世界空间,而 \(\textbf{t}_M\) 则是模型空间轴在世界空间的位移。
表面视觉性质的描述
表面性质包括光和表面交互作用的方式,包括漫反射颜色(diffuse color),粗糙度(roughness),光滑度(shininess),反射率(reflectivity),纹理,透明度/不透明度,折射率(refractive index)等。
光和颜色概论
光的颜色由其强度(intensity)\(I\) 及波长(wavelength)\(\lambda\) 所决定。光的行为,部分是由其穿过的介质(medium)所控制的,部分是由两种不同的介质之间的界面(interface)所控制的。
不过从技术的角度来看,不管光的行为有多复杂,其实光只能做四件事情
- 光可被吸收(absorb)
- 光可被反射(reflect)
- 漫反射(diffuse)是指入射光会向所有方向平均散射
- 镜面反射(specular)是指入射光直接被反射,或在反射时展开成很窄的椎体
- 光可在物体中传播(transmit),过程中通常会被折射(refract)
- 当光穿过物体时,光可能会被散射(半透明物质)
- 部分被吸收(如彩色玻璃)
- 或被折射(三棱镜)
- 也能先进入半固态表面,在表面下反弹,再从另一个位置离开表面。此称为次表面散射(SSS,subsurface scattering)
- 通过很窄的缺口时,光会被衍射(diffract)
颜色空间和颜色模型
颜色模型(color model)是量度颜色的三维坐标系统。而颜色空间(color space)是一个具体的标准,描述某颜色空间的数值化颜色如何映射至人类在真实世界中看到的颜色。
顶点属性
要描述表面的视觉特性,最简单的方法是把这些特性记录在表面的离散点上。网格的顶点是储存表面特性的便利位置,这种存储方式称为顶点属性(vertex attribute)。
- 位置矢量(position vector):\(\textbf{p}_i = [p_{ix}, p_{iy}, p_{iz}]\),网格中第 \(i\) 个定点的三维位置。位置矢量通常用物体的局部空间坐标表示。
- 顶点法矢量(vertex normal):\(\textbf{n}_i = [n_{ix}, n_{iy}, n_{iz}]\),顶点 \(i\) 位置上的表面单位矢量。用于计算动态光照。
- 顶点切线矢量(vertex tangent):\(\textbf{t}_i = [t_{ix}, t_{iy}, t_{iz}]\),这是和顶点副切线矢量(vertex bitangent)\(\textbf{b}_i = [b_{ix}, b_{iy}, b_{iz}]\)相互垂直的单位矢量,它们同时垂直于顶点法矢量 \(\textbf{n}_i\),这三个矢量 \(\textbf{n}_i, \textbf{t}_i, \textbf{b}_i\) 一起定义称为切线空间的坐标轴。此空间用于计算多种逐像素光照,法线贴图,环境贴图等。
- 漫反射颜色(diffuse color):\(\textbf{d}_i = [d_{Ri}, d_{Gi}, d_{Bi}, d_{Ai}]\),四元素颜色矢量。
- 镜面颜色(specular color):\(\textbf{s}_i = [s_{Ri}, s_{Gi}, s_{Bi}, s_{Ai}]\),描述其镜面高光的颜色。
- 纹理坐标(texture coordinates):\(\textbf{u}_{ij} = [u_{ij}, v_{ij}]\),用于把二维的位图“收缩包裹”在网格的表面,此过程称为纹理贴图(texture mapping)。
- 蒙皮权重(skinning weight):\((k_{ij}, w_{ij})\),在骨骼动画里,网格的顶点依附在骨骼的个别关节上,每个顶点需要指明其依附着的关节索引 \(k\)。另一种情况是,一个顶点受多个关节所影响,最终的顶点位置变为这些影响的加权平均。每个关节影响用权重因子 \(w\) 表示,所以顶点 \(i\) 可以受到顶点 \(j\) 所影响,其影响权重为 \(w_{ij}\)。
当渲染三角形时,重要的是三角形内点的视觉特性,这些内点最终成为屏幕上的像素。要取得网格表面的每像素属性,最简单的方法是对顶点属性进行线性插值。当把线性插值施于顶点颜色,这种插值便称为高氏着色法(Gouraud shading)。
光照基础
着色(shading)一词,通常是光照加上其他视觉效果的泛称。
局部及全局光照模型
渲染引擎用多种数学模型来模拟光合表面/体积的交互作用,这些模型称为光传输模型(light transport model)。最简单的模型只考虑直接光照(direct lighting),在此模型中,光发射后,碰到场景中的某个物体后会反射,然后直接进入虚拟摄像机的虚拟平面,这种简单的模型又称为局部光照模型(local illumination model),因为其只考虑光对于单个物体的局部影响。
要达到真实的写照效果,就必须考虑间接光照(indirect lighting),即光被多个表面反射后才进入摄像机,照顾到间接光照的模型称为全局光照模型(global illumination model)。
全局光照模型能够完全由单一的数学公式描述,此公式称为渲染方程或着色方程。
Phong氏光照模型
游戏引擎中最常用的局部光照模型是 Phong 氏反射模型(Phong reflection model)。此模型把从表面反射的光分解为三个独立项。
- 环境(ambient)项模拟场景中的光照水平。此乃场景中间接反射光的粗略估计,使阴影部分不会变成全黑。
- 漫反射(diffuse)项模拟直接光源在表面均匀地向各个方向反射。此项能逼近真光源照射至哑光表面的反射,比如木块或布料。
- 镜面反射(specular)项模拟在光滑表面看到的高光,镜面高光会出现在光源的直接反射方向。

Phong 氏模型输入如下
- 视线方向矢量 \(\textbf{V} = [V_x, V_y, V_z]\) 是从反射点延伸至虚拟摄像机焦点的方向。
- 三个颜色痛到的环境光强度 \(\textbf{A} = [A_R, A_G, A_B]\)。
- 光线到达表面上那一点的表面法线 \(\textbf{N} = [N_x, N_y, N_z]\)。
- 表面的反射属性,包括
- 环境反射量 \(k_A\)
- 漫反射量 \(k_D\)
- 镜面反射量 \(k_S\)
- 镜面的光滑度幂 \(\alpha\)
- 每个光源 \(i\) 的属性,包括
- 光源的颜色及强度 \(\textbf{C}_i = [C_{Ri}, C_{Gi}, C_{Bi}]\)
- 从反射点至光源的方向矢量 \(\textbf{L}_i\)
Phong 氏模型中,从表面上某点反射的光强度 \(\textbf{I}\) 可以表示为以下的矢量方程
\[ \textbf{I} = k_A \textbf{A}+ \sum_i [k_D (\textbf{N} \cdot \textbf{L}_i) + k_S(\textbf{R}_i \cdot \textbf{V})^\alpha]\textbf{C}_i \]
其中 \(\textbf{R}_i = [R_{xi}, R_{yi}, R_{zi}]\) 是光线方向 \(\textbf{L}_i\) 对于表面法线的反射。其中 \(\textbf{R}\) 的计算方式如下
\[ \begin{align} \textbf{L} &= \textbf{L}_T + \textbf{L}_N \\ \textbf{R} &= \textbf{L}_N - \textbf{L}_T \\ &= \textbf{L}_N - (\textbf{L} - \textbf{L}_N) \\ &= 2 \textbf{L}_N - \textbf{L} \\ &= 2(\textbf{N} \cdot \textbf{L}) \textbf{N} - \textbf{L} \end{align} \]
光源模型
- 环境光(ambient light):对应于 Phong 模型中的环境项。此项独立于视觉,并且不含方向。环境光由单个颜色 \(\textbf{A}\) 表示。
- 平行光(directional light):模拟距离受光表面接近无限远的光源,比如太阳。平行光以光源的颜色 \(\textbf{C}\) 和方向 \(\textbf{L}\) 表示。
- 点光 / 全向光(point light / omni-directional light):在游戏世界中有特定的位置,并向所有方向均匀投射。
- 聚光(spot light):等同于发射光线受限于一个圆锥范围的点光,以聚光位置 \(\textbf{P}\),光源颜色 \(\textbf{C}\),中央方向矢量 \(\textbf{L}\),最大半径 \(r_{max}\),内外圆锥角 \(\theta_{min}\) 和 \(\theta_{max}\) 表示。
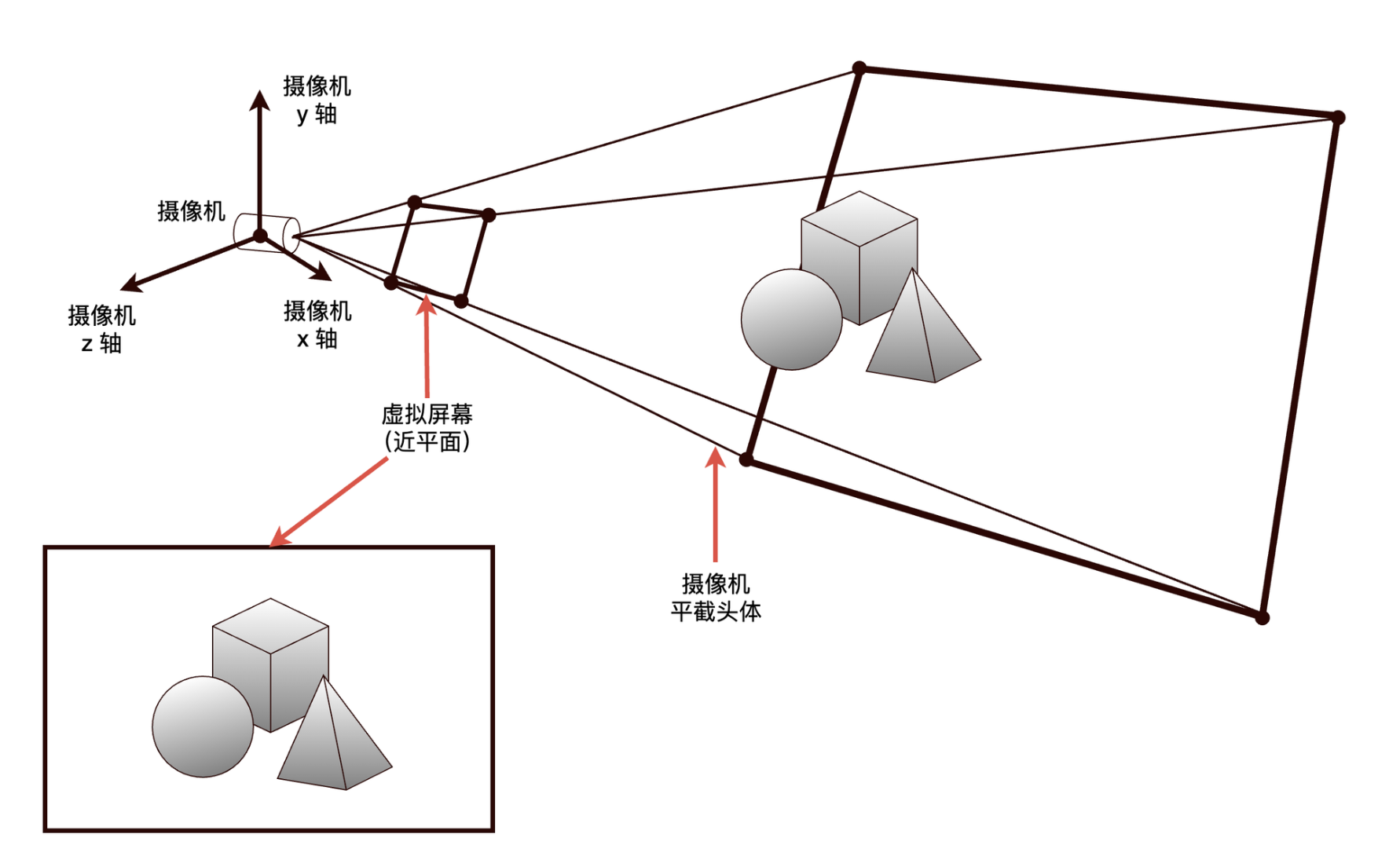
虚拟摄像机
虚拟摄像机是把摄像机看成是一个理想的焦点,并有一个矩形虚拟感光表面——称为成像矩形(imaging rectangle)——悬浮在焦点的近距离前面。成像矩形由正方形或矩形虚拟感光元件的栅格组成,每个感光元件对应屏幕中一个像素。所谓渲染,可以理解为每个虚拟感光元件记录光强度和颜色的过程。
观察空间
虚拟摄像机的焦点,是观察空间(view space)或称为摄像机空间(camera space)的三维坐标系统的原点。

摄像机位置及定向可以用观察至世界矩阵表示。当渲染三角形网格,其顶点首先从模型空间转换至世界空间,然后再从世界空间变换为观察空间。
\[ \textbf{M}_{M \to V} = \textbf{M}_{M \to W}\textbf{M}_{W \to V} = \textbf{M}_\text{model-view} \]
投影
投影(projection)将三维场景渲染成二维影像。
- 透视投影(perspective projection)模仿典型摄像机的成像方式,使用这种投影的时候,物体近大远小。此效果称为透视收缩(perspective foreshortening)。
- 正射投影(orthographic projection)维持长度不变,主要用于渲染平面图。
平截头体(frustum)
平截头体是摄像机能“看到”的空间,也是观察体积(view volume)。观察体积由六个平面定义。
- 近平面(near plane)对应于摄像机感光元件的表面。
- 上下左右四个平面是虚拟屏幕的边缘。
- 远平面(far plane)则用作渲染优化,确保很远的物体不被渲染。
齐次裁剪空间
透视及正射投影能把点从观察空间变换至一个称为齐次裁剪空间(homogeneous clip space)的坐标系。此三维空间仅是观察空间的变形版本。裁剪空间是用来把摄像机空间的观察体积转换为标准的观察体积,转换后的体积不仅独立于把三维场景转换成二维屏幕空间的投影类型,也独立于屏幕的分辨率(resolution)和长宽比(aspect ratio)。
裁剪空间中,标准观察体积是一个长方体,\(x\) 轴和 \(y\) 轴的范围是 \([-1, 1]\),\(z\) 轴的范围在 OpenGL 是\([-1, 1]\),在 DirectX 里是\([0, 1]\)

齐次裁剪空间的标准观察体积
透视投影矩阵将点从观察空间变换至齐次裁剪空间,令近平面在 \(z\) 轴相交于 \(-n\),远平面相交于 \(-f\),虚拟屏幕左右上下分别位于近平面的 \(x = l, x = r, y = b, y = t\)。则透视投影矩阵为
\[ \textbf{M}_{V \to H} = \begin{bmatrix} \cfrac{2n}{r-l} & 0 & 0 & 0 \\ \\ 0 & \cfrac{2n}{t-b} & 0 & 0 \\ \\ \cfrac{r+l}{r-l} & \cfrac{t+b}{t-b} & -\cfrac{f+n}{f-n} & -1 \\ \\ 0 & 0 & -\cfrac{2nf}{f-n} & 0 \end{bmatrix} \]
进行透视投影后,每个顶点的 \(x\) 和 \(y\) 坐标会除以其 \(z\) 坐标,这个除法是产生透视收缩的方法。将观察空间的点 \(\textbf{p}_V\) 转化为齐次坐标再乘以透视投影矩阵,有
$$ _H = V {V H} = \[\begin{bmatrix} p_{V_x} & p_{V_y} & p_{V_z} & 1 \end{bmatrix} \begin{bmatrix} \cfrac{2n}{r-l} & 0 & 0 & 0 \\ \\ 0 & \cfrac{2n}{t-b} & 0 & 0 \\ \\ \cfrac{r+l}{r-l} & \cfrac{t+b}{t-b} & -\cfrac{f+n}{f-n} & -1 \\ \\ 0 & 0 & -\cfrac{2nf}{f-n} & 0 \end{bmatrix}\]$$
其结果是以下的形式
\[ \textbf{p}_H = \begin{bmatrix} a & b & c & -p_{V_z} \end{bmatrix} \]
转换为三维坐标的时候,除以第四维分量即可
\[ \begin{align} \textbf{p}_H &= \begin{bmatrix} \cfrac{a}{-p_{V_z}} & \cfrac{b}{-p_{V_z}} & \cfrac{c}{-p_{V_z}} \end{bmatrix} \\ &= \begin{bmatrix} p_{H_x} & p_{H_y} & p_{H_z} \end{bmatrix} \end{align} \]
正射投影矩阵如下所示
\[ \textbf{M}_{V \to H} = \begin{bmatrix} \cfrac{2}{r-l} & 0 & 0 & 0 \\ \\ 0 & \cfrac{2}{t-b} & 0 & 0 \\ \\ 0 & 0 & -\cfrac{2}{f-n} & 0 \\ \\ -\cfrac{r+l}{r-l} & -\cfrac{t+b}{t-b} & -\cfrac{f+n}{f-n} & 1 \end{bmatrix} \]
三角形光栅化(rasterization)
要在屏幕上产生一个三角形影像,我们需要给该三角形范围内的像素填充数据。此过程称为光栅化。光栅化过程中,三角形表面会拆分成名为片段(fragment)的小块,每个片段对应三角形表面中的一个细小区域,而每个这些细小区域对应单个屏幕像素。
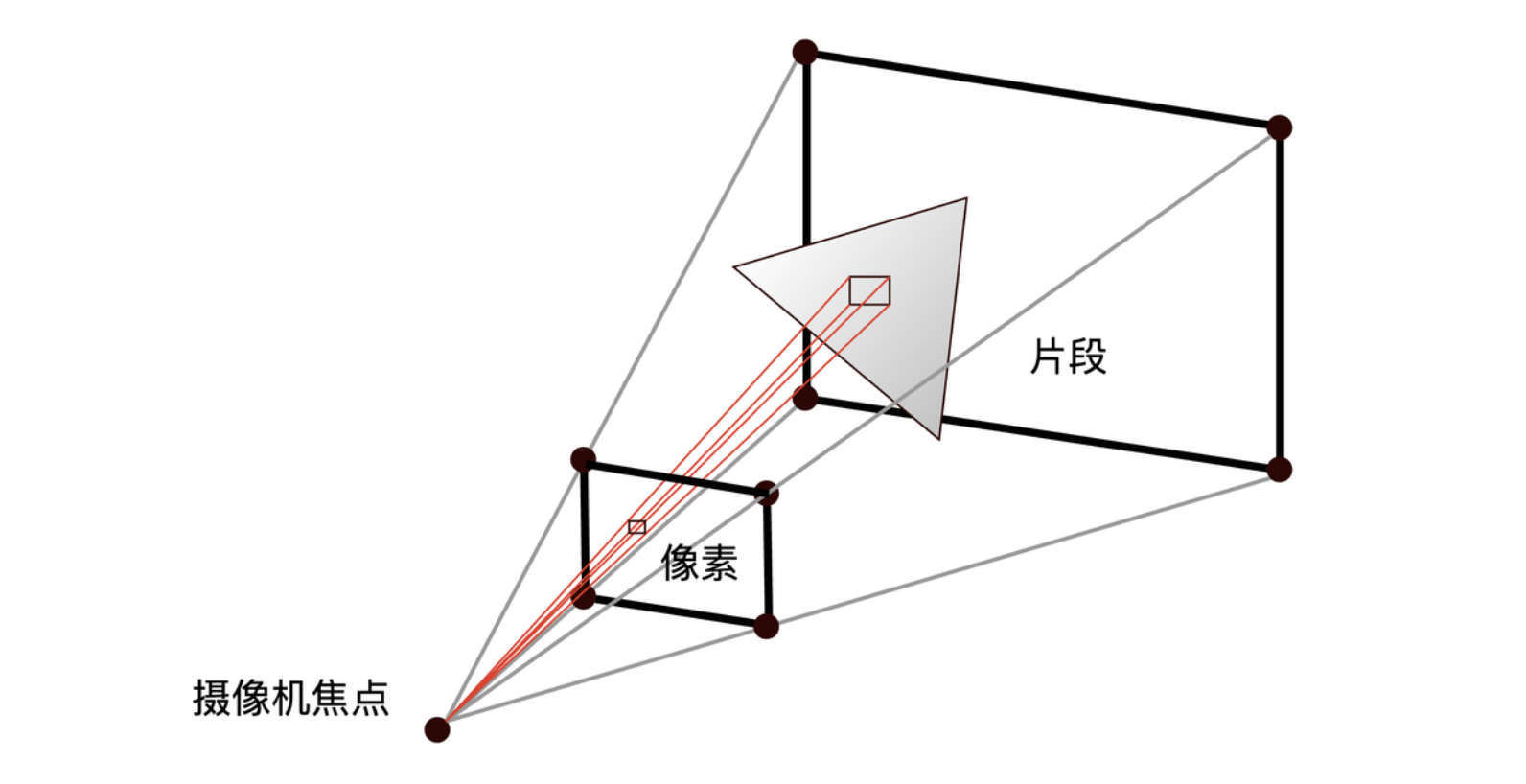
抗锯齿(antialiasing)是一种降低由混合所形成的视觉缺乏的技术。抗锯齿的效果是,三角形与帧缓冲附近的颜色混合起来。
要正确实现三角形的遮挡关系,不需要理会三角形的渲染次序,渲染引擎会使用称为深度缓冲(depth buffer)的技术。每个片段含有一个 \(z\) 坐标,以量度其“深入”屏幕的深度。
在渲染两个非常相近的平面的时候,渲染引擎必须能够区分两个平面的深度。深度缓冲仅有有限的精确度,因此两个足够接近的平面,其两个深度可能会变成相同的离散值,这样较远的平面就会“刺穿”较近的平面,造成一个称为深度冲突(z-fighting)的噪点效果。要解决这个问题,深度应该使用观察空间中的 \(z\) 坐标而非齐次裁剪空间的 \(z\) 坐标,这种技术也称为 \(w\) 缓冲。
渲染管道
高级渲染步骤是由名为管道(pipeline)的软件架构所实现的。管道只是一连串顺序计算阶段,每个阶段有其具体目的,每个阶段会操作输入流中的数据项,并对输出流产生数据。管道中的每个阶段通常会独立于其他阶段,因此,非常适合并行化。
渲染管道概览如下
- 工具阶段(脱机):定义几何的表面特性(材质)。
- 资产调节阶段(脱机):资产调节管道处理几何和材质数据,生成引擎可用的格式。
- 应用程序阶段(CPU):识别出潜在可视的网格实例,并把它们及其材质呈交至图形硬件以供渲染。
- 几何阶段(GPU):把顶点变换,照明,然后投影至齐次裁剪空间。用几何着色器处理三角形,然后对三角形根据平截头体进行裁剪。
- 光栅化阶段(GPU):把三角形转化为片段,并对片段进行着色。片段经过多种测试后(深度测试,alpha 测试,模板测试等),最终和帧缓冲混合。
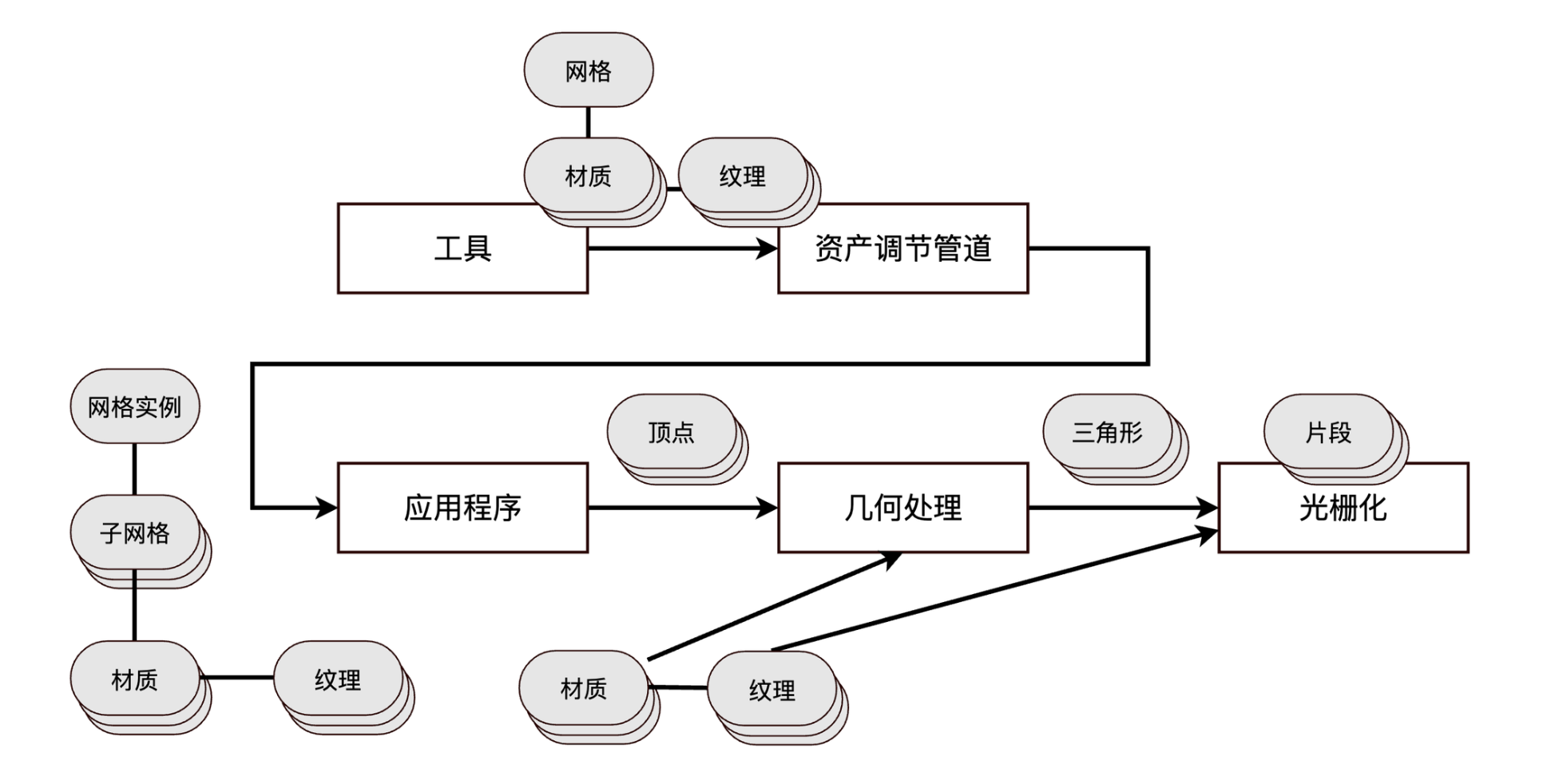
GPU 渲染管道
典型 GPU 渲染管道实现的几何处理及光栅化阶段。
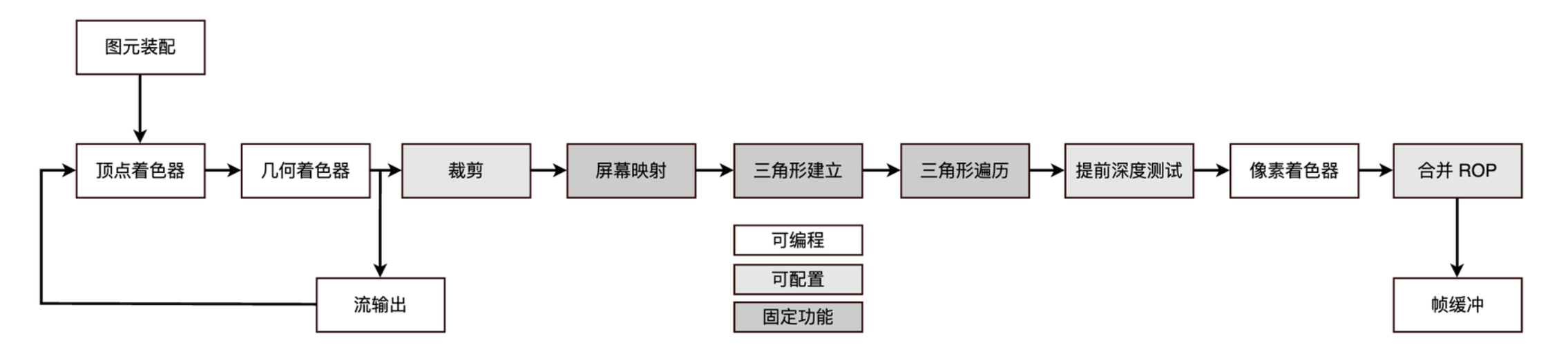
- 顶点着色器:此阶段完全可以编程,负责变换及着色 /
光照顶点。
- 进行透视投影
- 每顶点光照及纹理计算
- 动画角色计算蒙皮
- 产生程序式动画
- 几何着色器:几何着色器处理以齐次裁剪空间表示的整个图元(三角形,线段,点)。
- 阴影体积拉伸
- 渲染立方体贴图
- 在网格的轮廓边缘拉伸毛发的鳍
- 从数据生成粒子四边形
- 动态镶嵌
- 流输出:现在的 GPU 允许把到达此阶段的数据写回内存。
- 裁剪:把三角形在平截头体以外的部分去掉。
- 屏幕映射:将顶点从齐次裁剪空间变换至屏幕空间。
- 三角形建立:光栅化硬件把三角形转换成片段。
- 三角形遍历:对顶点属性进行插值,以产生每片段属性,供像素着色器使用。
- 提前深度测试:检测片段是否需要被丢弃。
- 像素着色器:替每个像素着色。
- 合并 / 光栅运算阶段(ROP,raster operations stage):负责多个片段测试,包括深度测试,alpha 测试,以及模板测试。
可编程着色器
着色器从输入数据取得一个元素,把该元素变换为输出数据的一个或多个元素。
- 顶点着色器的输入为顶点,包含以模型空间或世界空间表示的位置及法矢量。输出为已变换及照明的顶点,以齐次裁剪空间表示。
- 几何着色器的输入为单个 \(n\) 顶点几何图元——点,线,三角形,以及最多 \(n\) 个作为控制点的额外顶点。其输出为 0 或者多个图元。
- 像素着色器的输入为片段,其属性来自对三角形顶点属性的插值。其输出是将要写至帧缓冲的颜色。
应用程序阶段
应用程序阶段驱动 GPU 管道渲染,本阶段有三个角色:
- 可见性判别:把可见(或至少潜在可见)的物体提交 GPU,以免浪费宝贵的资源渲染总是看不见的物体。
- 提交几何图元至 GPU 以供渲染:把子网格材质对传送至 GPU。
- 控制着色器参数及渲染状态:uniform 参数通过常数寄存器传送至着色器时,应用程序阶段按每个图元为单位进行配置。
高级光照和全局光照
基于图像的光照
许多高级的光照及着色技术都会大量使用影像数据,这些数据通常是以二维纹理贴图形式表示的。这些技术统称为基于图像的光照(image-based lighting)算法。
高动态范围光照
高动态范围(HDR,high dynamic range)光照尝试捕捉真实世界的光照强度,而不限于从 0 到 1。把影像显示于屏幕之前,还需要进行一个色调映射(tone mapping)处理,把影像的强度调整至显示设备所支持的范围。
全局光照
全局光照是指一类光照算法,这些算法考虑到光从光源传送至虚拟摄像机之间与多个物体的互动。
阴影渲染
最流行的两种渲染技巧分别为阴影体积(shadow volume)和阴影贴图(shadow map)。两种技巧中,都会把场景中的物体分为 3 个类别:投射阴影的物体,接收阴影的物体,以及完全被阴影渲染忽略的物体。
阴影体积
在阴影体积技术中,会从产生阴影的光源位置观察每个投射阴影的物体,在那个视觉判断物体的轮廓边缘。这些边缘沿光线方向伸出一个几何立体,该几何立体代表着光线被阴影物体遮挡所造成的空间体积。
渲染的时候要先渲染一次没有阴影的场景,同时填充准确的深度缓冲。然后把模板缓冲清空,再从摄像机的视觉渲染阴影体积。
阴影贴图
进行每片段深度测试,但该“深度”非从摄像机的视角去计算,而是从光源的视觉计算。使用阴影贴图时,需要把场景渲染两次,首先,从光源视觉渲染场景,把结果的深度缓冲存储为阴影贴图纹理。然后,以正常方式渲染场景,渲染每个判断时用阴影贴图判断该片段是否在阴影内。
视觉效果和覆盖层
上面所说的渲染管道,主要是用于渲染三维固体物体的。通常在此渲染管道之上,还有一些专门渲染视觉效果的渲染系统,例如例子效果,贴花(比如弹孔,裂缝,抓痕),头发皮毛,降雨降雪,水,以及其他专门的视觉效果。
粒子效果
粒子渲染系统是为了渲染无固定形状的物体而设置的,具有以下的特点:
- 粒子系统由大量相对简单的几何物体所组成。
- 几何物体通常是朝向摄像机的。
- 其材质几乎是半透明的,因此,粒子系统有严格的渲染次序。
- 粒子以多种丰富的方式表现动画。
- 粒子通常会不断出生及湮灭,粒子发射器是游戏世界中的逻辑实体,以用户设置的速率创造粒子。
贴花(decal)
贴花是覆盖在场景中正常物体上,相对较小的几何物体,用于动态改变物体表面的外观。
环境效果
比如天空,地形,水体等。
覆盖层
游戏内图形用户界面及菜单系统。
全屏后期处理效果
全屏后期处理效果应用在已渲染的三维场景上,以增加真实感或做出特殊的风格。
- 动态模糊(motion blur)
- 景深模糊(depth-of-field blur)
- 晕影(vignette)
- 着色(colorization)