多元函数

发表于 2022-01-23 分类于 Math Disqus：本文字数： 3.1k 阅读时长 ≈ 11 分钟

这部分对一元函数的各定理进行推广重述。并加入多元函数的集合基础，以及推广时候需要注意的地方。

基本概念

集合相关概念

下面简略给出集合相关的定义，更严格的定义在拓扑方面的总结里给出。

邻域

在不同上下文里，对邻域的概念定义可能会有所不同，直观上来说，对于 n 维空间中的某个点 $M(x_1, x_2, \cdots, x_n)$，其邻域就是其附近的区域，这样的区域可以是不规则的，比如：

\[ \{ M'(x'_1, x'_2, \cdots, x'_n) | x'_i \in (x_i - \delta_i, x_i + \delta_i), i \in [1, n], \delta_i \in \mathbb{R} \} \]

也可以是规则的立方体，

\[ \{ M'(x'_1, x'_2, \cdots, x'_n) | x'_i \in (x_i - \delta, x_i + \delta), i \in [1, n], \delta \in \mathbb{R} \} \]

或者球体

\[ \{ M'(x'_1, x'_2, \cdots, x'_n) | \sqrt{\sum_{i = 1}^n(x'_i - x_i)^2} < r, i \in [1, n], r \in \mathbb{R} \} \]

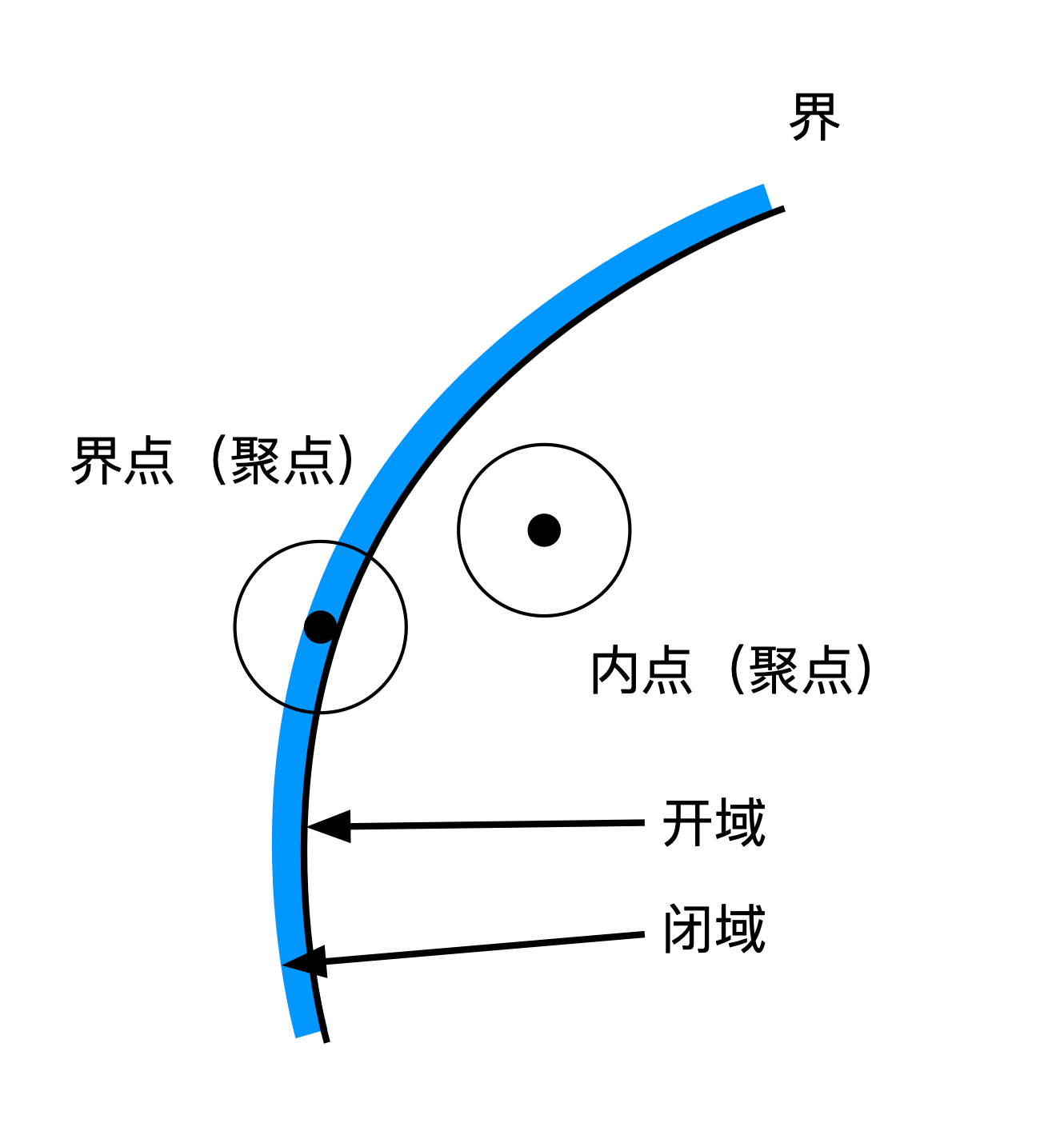
内点

若点 $M(x_1, x_2, \cdots, x_n)$ 连同它充分小的邻域都属于（n 维空间内的）集 $\mathcal{M}$，则称点 $M$ 为集 $\mathcal{M}$ 的内点。

聚点

若在点 $M_0$ 的任一邻域（不论什么类型）内总包含集 $\mathcal{M}$ 中的至少一个异于 $M_0$ 的点，则点 $M_0$ 为集 $\mathcal{M}$ 的聚点。（注意，$M_0$ 不一定需要在 $\mathcal{M}$ 里的）

开域

完全由内点组成的集称为开域。

界

开域的聚点而不属于这个域的点称为其界。

闭域

开域连同其界称为闭域。

内点和界点都是聚点，而不属于开集的聚点为边界，开集加边界为闭集。

注意到，内点存在能完全在开集内的邻域，而非内点不行，界点不可能存在完全包含于开集里的邻域。（可以通过一维闭区间的端点来想象）

有界点集

如果点集 $\mathcal{M}$ 全部包含于一个有限邻域内，则称为有界。

连通域

如果域中的任意两点，可以通过一些连续的折线来连接（而这些折线也在域内），则这个域就称为连通域。

多元函数定义

设有 $n$ 个变量 $x_1, x_2, \cdots, x_n$，它们的协同值可以从 $n$ 维空间中的某一点集 $\mathcal{M}$ 任意选取，这些变量称为自变量。若用 $M$ 表示点 $(x_1, x_2, \cdots, x_n)$，则这些变量的函数 $u = f(M) = f(x_1, x_2, \cdots, x_n)$ 称为多元函数。

多元函数极限

假定函数 $f(x_1, x_2, \cdots, x_n)$ 是在具有聚点 $M_0(a_1, a_2, \cdots, a_n)$ 的某一点集 $\mathcal{M}$ 内定义的。当变量 $x_1, x_2, \cdots, x_n$ 依次趋向 $a_1, a_2, \cdots, a_n$ 的时候，如果对于任一数 $\varepsilon > 0$，能找到对应的 $\delta > 0$，使得1q

\[ |x_1 - a_1| < \delta, \cdots, |x_n - a_n| < \delta, \]

就能使

\[ |f(x_1, x_2, \cdots, x_n) - A| < \varepsilon \]

就称函数 $f$ 在点 $M_0$ 处以 $A$ 为极限。并记作，

\[ A = \lim_{\scriptsize \begin{aligned} x_1 &\to a_1 \\ &\cdots \\ x_n &\to a_n \\ \end{aligned} } f(x_1, x_2, \cdots, x_n) \]

使用整序变量的语言，考察 $n$ 维空间中的点列

\[ \{M_k(x_1^{(k)}, x_2^{(k)}, \cdots, x_n^{(k)})\}, k \in \mathbb{Z}^+ \]

若当 $k \to +\infty$ 时距离

\[ \over{M_0M_k} \to 0 \]

则点列收敛于极限点 $M_0(a_1, a_2, \cdots, a_n)$。另外，也可以令 $x_i^{(k)} \to a_i$ 来达到同一效果。

n 重极限

上述极限在个变元同时趋向各自的极限时得出的，称为 $n$ 重极限。

累次极限

如果各变元依次趋向极限，则称为累次极限。

两种极限的关系

下面用二重极限来叙述这种关系。如果二重极限

\[ A = \lim_{\scriptsize \begin{aligned} x &\to a \\ y &\to b \\ \end{aligned} } f(x, y) \]

存在，并且对于 $\mathcal{Y}$ 内的任一 $y$ 有依 $x$ 的（有限的）单重极限

\[ \varphi(y) = \lim_{x \to 0} f(x, y) \]

存在，则累次极限

\[ \lim_{y \to b} \varphi(y) = \lim_{y \to b}\lim_{x \to a} f(x, y) \]

存在，并且等于二重极限。

连续函数

多元函数的连续与间断为一元函数的推广。设函数 $f(x_1, x_2, \cdots, x_n)$ 定义于 $n$ 维空间的某一点集 $\mathcal{M}$，又设 $M'(x'_1, \cdots, x'_n)$ 是这集的聚点并且属于这集（也就是内点）。若

\[ \lim_{\scriptsize \begin{aligned} x_1 &\to x'_1 \\ &\cdots \\ x_n &\to x'_n \\ \end{aligned} } f(x_1, x_2, \cdots, x_n) = f(x'_1, x'_2, \cdots, x'_n) \]

成立，就说函数 $f(x_1, x_2, \cdots, x_n)$ 在点 $M'(x'_1, x'_2, \cdots, x'_n)$ 处是连续的，否则，就说函数在点 $M'$ 处有间断。

下面将一元函数的各定理转述为多元函数的版本。

零值定理

布尔查诺 - 柯西第一定理 设函数 $f(M)$ 是在连通域 $\mathcal{D}$ 中连续，若在这域中有两点 $M_1$ 以及 $M_2$ 的函数值异号，不失一般性，有

\[ f(M_1) < 0, f(M_2) > 0 \]

则在域中定能找到一点 $M$，有 $f(M) = 0$。

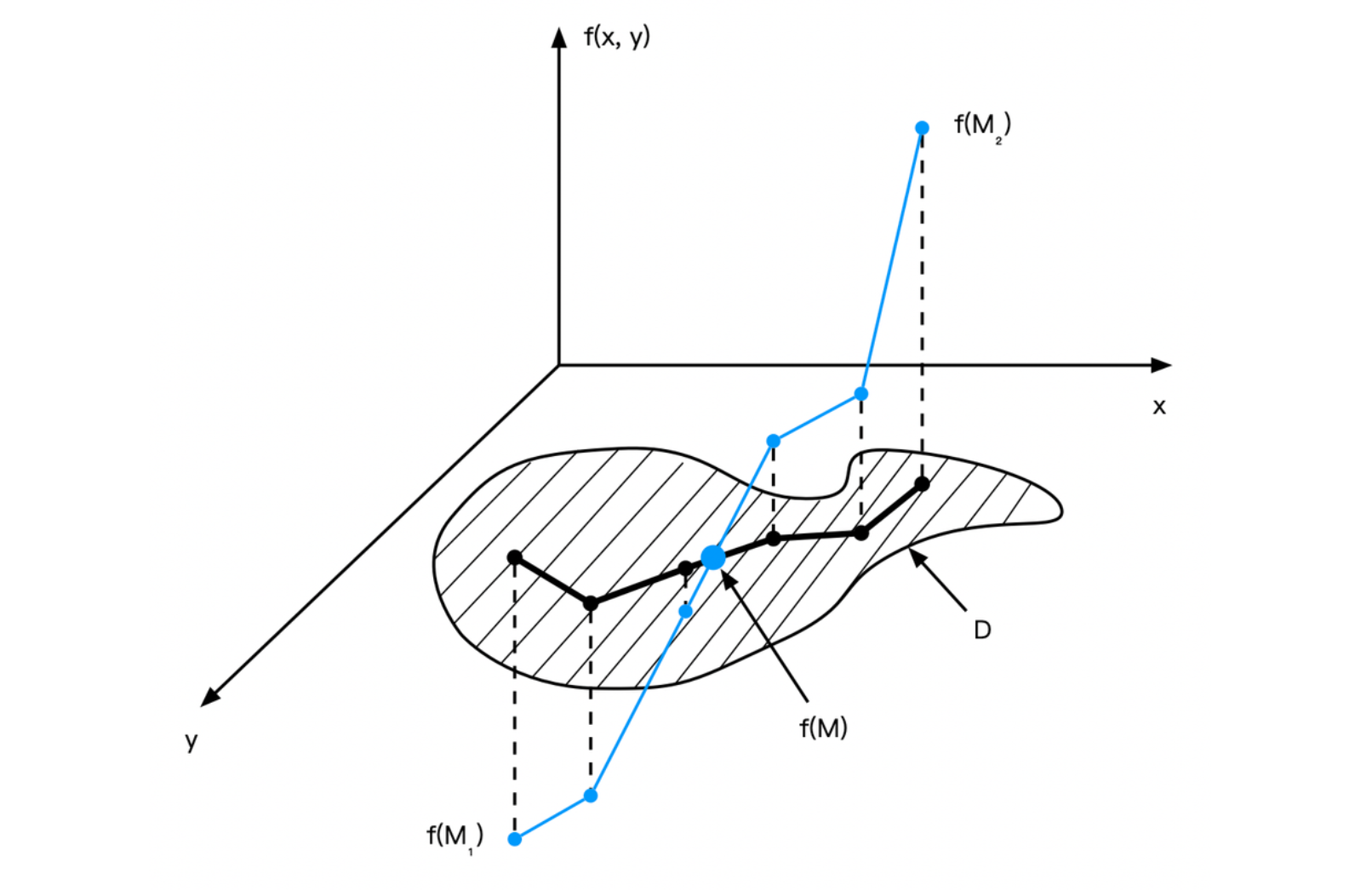
介值定理

布尔查诺 - 柯西第二定理 设函数 $f(M)$ 是在连通域 $\mathcal{D}$ 中连续，若在这域中有两点 $M_1$ 以及 $M_2$ 处有不同的函数值，不失一般性，有

\[ f(M_1) = a, f(M_2) = b \]

则在域中定能找到一点 $M$，有 $f(M) = c$，其中 $a < c < b$。

布尔查诺 - 魏尔斯特拉斯引理

这是套区间引理的多元函数版本。由任一有界点列

\[ M_1, M_2, \cdots, M_n, \cdots \]

中恒能选出收敛于极限点的部分点列

\[ M_{n_1}, M_{n_2}, \cdots, M_{n_k}, \cdots (n_1 < n_2 < \cdots < n_k \to +\infty) \]

闭区间有界性

魏尔斯特拉斯第一定理 若函数 $f(M)$ 是定义在有界闭域 $\mathcal{D}$ 中并且是连续的，则它必是有界的，即必存在着有限的常数 $a$ 以及 $b$，使当 $M \in \mathcal{D}$ 时，有 $a \leq f(M) \leq b$。

魏尔斯特拉斯第二定理 若函数 $f(M)$ 是定义在有界闭域 $\mathcal{D}$ 中并且是连续的，则它在这区间内必能达到自己的上确界以及下确界。

一致连续

设函数 $f(M)$ 在整个集 $\mathcal{M}$ 内连续，对于任意的 $\varepsilon > 0$，以及任意的 $M \in \mathcal{M}$，存在 $\delta > 0$，对于 $M' \neq M$，使得只要 $|M - M'| < \delta$，就有 $|f(M) - f(M')| < \varepsilon$。这就称函数 $f(M)$ 在 $\mathcal{M}$ 内一致连续。

康托定理

若函数 $f(x, y)$ 在有界闭区域 $\mathcal{D}$ 中连续，则它在 $\mathcal{D}$ 中也是必为一致连续的。

博雷尔引理

设平面上有若干个开域 $\sigma$ 所成的系 $\Sigma$，若集 $\mathcal{M}$ 内的每一点至少被其中一个 $\sigma$ 所包含着，则说系 $\Sigma$ 覆盖集 $\mathcal{M}$。若平面上的点的有界闭集 $\mathcal{M}$ 能被开域 $\sigma$ 的无穷系 $\Sigma = \{ \sigma \}$ 所覆盖，则恒能从中选出有限子系

\[ \Sigma^* = \{ \sigma_1, \sigma_2, \cdots, \sigma_n \} \]

它也能覆盖全部集 $\mathcal{M}$。

导数与微分

不失一般性，下面以三元函数来表述。

偏导数

设某一区域 $\mathcal{D}$ 中有函数 $u = f(x, y, z)$；在这区域中取一点 $M_0(x_0, y_0, z_0)$。若我们给 $y$ 以及 $z$ 以常数值 $y_0$ 以及 $z_0$ 而让 $x$ 变动，则 $u$ 变成一个变元 $x$ 的函数（在 $x_0$ 的邻域内），给数值 $x_0$ 以增量 $\Delta x$，则函数就得到增量

\[ \Delta_x u = \Delta_x f(x_0, y_0, z_0) = f(x_0 + \Delta x, y_0, z_0) - f(x_0, y_0, z_0) \]

因为 $\Delta_x u$ 是仅由于一个变元的数值变动而产生的，故它可以称为函数（关于 $x$）的偏增量，导数

\[ \lim_{\Delta x \to 0} \frac{\Delta_x u}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x, y_0, z_0) - f(x_0, y_0, z_0)}{\Delta x} \]

就称为函数 $f(x, y, z)$ 在点 $f(x_0, y_0, z_0)$ 处关于 $x$ 的偏导数，有时候也记作下面的形式

$$ , , u'_x, f'_x(x_0, y_0, z_0)

偏微分

偏导数 $\partial u / \partial x$ 乘以任意增量 $\Delta x$ 的积称为函数 $u$ 关于 $x$ 的偏微分，用记号

\[ d_x u = \frac{\partial u}{\partial x} \cdot \Delta x \]

表示。用 $dx$ 表示增量也可以。

全增量

若从自变量的值 $x_0, y_0, z_0$ 出发，依次给三者增量 $\Delta x, \Delta y, \Delta z$，则函数 $u = f(x, y,z )$ 的增量

\[ \Delta u = \Delta f(x_0, y_0, z_0) = f(x_0 + \Delta x, y_0 + \Delta y, z_0 + \Delta z) - f(x_0, y_0, z_0) \]

称为函数的全增量。

若偏导数 $f'_x(x, y, z), f'_y(x, y, z), f'_z(x, y, z)$ 不仅在点 $(x_0, y_0, z_0)$ 处存在，并在它的某一邻域内也存在，此外，它们（作为 $x, y, z$ 的函数）在这点为连续，则下式成立

\[ \begin{aligned} \Delta u &= \Delta f(x_0, y_0, z_0) \\ &= f'_x(x_0, y_0, z_0) \cdot \Delta x + f'_y(x_0, y_0, z_0) \cdot \Delta y + f'_z(x_0, y_0, z_0) \cdot \Delta z + \\ &\ \ \ \ \ \ \alpha \cdot \Delta x + \beta \cdot \Delta y + \gamma \cdot \Delta z \end{aligned} \]

复合函数的导数

设函数 $u = f(x, y, z)$ 定义于区域 $\mathcal{D}$ 内，而且每一变元 $x, y, z$ 又各为变动于某一区间内的变量 $t$ 的函数：

\[ x = \varphi(t), \ \ y = \psi(t), \ \ z = \chi(t) \]

此外，再设当 $t$ 变动时点 $(x, y, z)$ 不超出 $\mathcal{D}$ 的变动范围，把 $x, y, z$ 代入得复合函数

\[ u = f(\varphi(t), \psi(t), \chi(t)) \]

假定 $u$ 有关于 $x, y, z$ 的连续偏导数 $u'_x, u'_y, u'_z$，且 $x'_t, y'_t, z'_t$ 都存在，那时就可以证明复合函数的导数必须存在，同时可以将其算出。

\[ \frac{\partial u}{\partial t} = \frac{\partial u}{\partial x} \cdot \frac{\partial x}{\partial t} + \frac{\partial u}{\partial y} \cdot \frac{\partial y}{\partial t} + \frac{\partial u}{\partial z} \cdot \frac{\partial z}{\partial t} \]

高阶导数

若函数 $u = f(x, y, z)$ 在某一区域 $\mathcal{D}$ 中有关于其中一个变元的偏导数，则这偏导数本身仍是 $x, y, z$ 的函数，故仍能在某一点 $(x_0, y_0, z_0)$ 有关于同一变元或另一变元的偏导数，这些后来得到的导数，对于原来的函数 $u$ 而言，就是二阶偏导数。例如，若一阶导数是关于 $x$ 取的，则其关于 $x, y, z$ 的二阶导数便记为

\[ \begin{aligned} \frac{\partial^2 u}{\partial x^2} &= \frac{\partial^2 f(x_0, y_0, z_0)}{\partial x^2} \\ \frac{\partial^2 u}{\partial x \partial y} &= \frac{\partial^2 f(x_0, y_0, z_0)}{\partial x \partial y} \\ \frac{\partial^2 u}{\partial y \partial z} &= \frac{\partial^2 f(x_0, y_0, z_0)}{\partial y \partial z} \end{aligned} \]

关于混合导数顺序的定理 假定函数 $f(x, y)$ 定义域区域 $\mathcal{D}$ 中，在区域中存在着一阶导数 $f'_x, f'_y$ 及二阶混合导数 $f''_{xy}$ 及 $f''_{yx}$，而且这些二阶导数作为 $x, y$ 的函数，它们在 $\mathcal{D}$ 中的某一点 $f(x_0, y_0)$ 连续，那么，在这点

\[ f''_{xy}(x_0, y_0) = f''_{yx}(x_0, y_0) \]

推广到一般情形 设 $n$ 元函数 $u = f(x_1, x_2, \cdots, x_n)$ 定义于 $n$ 维域 $\mathcal{D}$ 中，且在这区域中有至 $(k - 1)$ 阶为止的一切可能的偏导数以及一切 $k$ 阶混合导数，而且所有这些导数在 $\mathcal{D}$ 中都为连续，在这些条件下，任一 $k$ 阶混合导数的数值就与进行逐次微分的次序无关。

极值与最值

设函数 $u = f(x_1, x_2, \cdots, x_n)$ 定义于区域 $\mathcal{D}$ 内，且 $(x^0_1, x^0_2, \cdots, x^0_n)$ 为内点。若在邻域

\[ (x^0_1 - \delta, x^0_1 + \delta; x^0_2 - \delta, x^0_2 + \delta; \cdots; x^0_n - \delta, x^0_n + \delta;) \]

中的一切点都有

\[ f(x_1, x_2, \cdots, x_n) \leq f(x^0_1, x^0_2, \cdots, x^0_n) \]

就说函数在该点处有极大值（或极小值）。

必要条件

在考察点 $(x^0_1, x^0_2, \cdots, x^0_n)$ 处如果存在有限偏导数，则一切的偏导数必须为 $0$，也就是

\[ f'_{x_1}(x^0_1, x^0_2, \cdots, x^0_n), \cdots, f'_{x_n}(x^0_1, x^0_2, \cdots, x^0_n) \]

均为 $0$。这是该点处存在极值的必要条件。

联立偏导数为 $0$ 的方程组可以求出那些怀疑有极值的静止点。

\[ \begin{cases} f'_{x_1}(x^0_1, x^0_2, \cdots, x^0_n) = 0, \\ f'_{x_2}(x^0_1, x^0_2, \cdots, x^0_n) = 0, \\ \cdots \\ f'_{x_n}(x^0_1, x^0_2, \cdots, x^0_n) = 0 \end{cases} \]

充要条件

充要条件与二次型性质相关。