数学分析概览
前言
一直不想放弃数学,一直想继续深入学习数学,最近重拾数学以来看了不少数学的子学科,感到有不少地方与之前的感觉不一样了。在高中时代,可能很喜欢挑战难题,快感源于能独自思考出解决的办法。而那些难题需要的知识点可能并不多,但是需要很巧妙的解决办法。到了大学,我依然没有改变学习数学的习惯,其实也并没有太系统与科学的方法,就只是看书以及刷题。现在回过头看,这种方式可能是一直以来阻碍我前进的原因。近代数学发展出了不少新的概念,这些概念相互交织,相互引用,而围绕这些概念的定理,更是层层相套,如果不从一个更宏观的视觉来看待问题,最后只会淹没在茫茫的定理当中。比如小时候,我们都是零散地记忆结论,比如三角形内角和为 180 度,比如导数大于零函数单调递增,又比如对于一般立体,满足顶点数 - 边数 + 面数恒等于 2。在碰到问题的时候,我们可能会非常零散地检索这些定理,看看那个定理比较适用,同时还会零散地搜索方法,比如数学归纳法,反证法等,靠经验将这些工具进行组合,然后解题。当然,这样的过程毫无问题,但这必须是另一个过程的结果,也就是站在高处,对各种定理以及结论的关系了如指掌之后的结果。
如果想持续深入地学习数学,就必须对所有的数学分支有一个非常清晰的认识,并且对这些分支里面独有的概念有深入的理解,纵观各数学分支,其实也不难发现有很多概念与方法都是融汇贯通的,比如拓扑学也好,函数论也好,都可以以朴素的集合论作为基础,又比如概率论里的连续概率计算,也需要到多元函数的知识等。而极限的概念,可谓贯穿各个学科,\(\varepsilon-\delta\) 语言基本上成为了各处需要连续性时候的严格定义。搞清楚这些概念,方便我们融汇贯通各分支的基本概念。而数学分支本身也是有层次的,不能否认像抽象代数这样的分支会处在比较高的层次上,因为抽象代数本身就是对众多数学分支进行抽象的科学。
本文的目的主要是理清数学分析中各种基本概念以及重要定理的逻辑关系,主要参考书目为菲赫金哥尔茨的《微积分学教程》以及柯朗的《微积分与数学分析引论》。由于不同的数学分析相关书籍范围可能不太一样,所以这里只是以上述的两本书为大概的范围。
研究对象及其关系
数学分析的研究对象,在我看来只有两个,“数”以及“函数”。而其中的“数”,主要是指“实数的连续统”,而不是抽象代数里面有关数的运算以及不变性相关的内容,也不会涉及到复数域,所以有时候,数学分析也会被称作实分析(当然这个说法也不太准确,只是一个惯例)。而“函数”,实际上是描述“数”与“数”之间的关系,在数学分析里会以初等函数开始,研究函数有关的一系列课题,比如函数本身的性质(单调性,连续性,凹凸性,极值,解等),又比如通过建立函数的函数(导数,微分)而反过来研究函数。而函数也可以自变量个数来分成一元函数以及多元函数等。
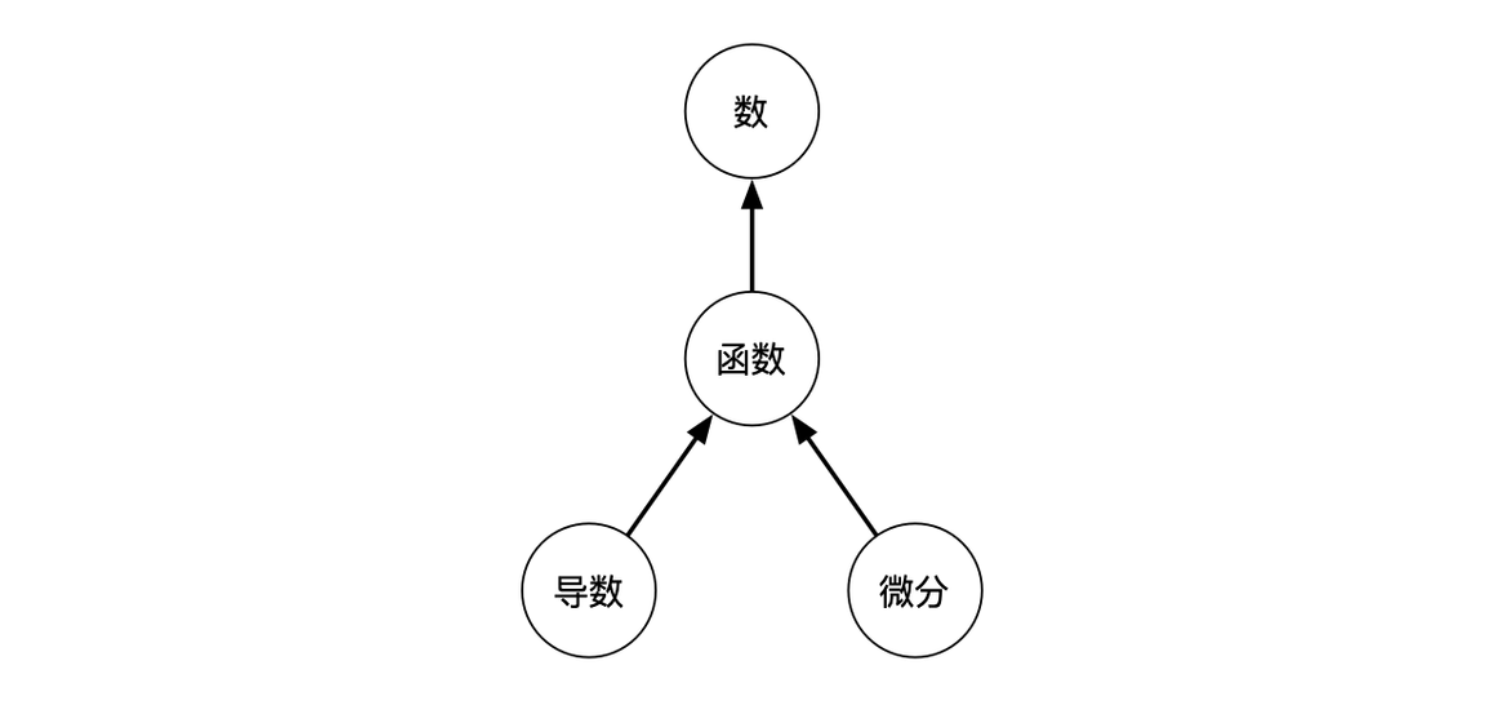
上图表明各主要研究对象之间的关系,箭头表明依赖方向。函数依赖于数,因为函数描述数之间的关系,定义域是数的集合,值域也是数的集合,定义域的连续性直接影响到了值域的连续性,也就影响了函数的连续性了。导数与微分,其实都是有关函数变化的研究,导数是变化率,微分是变化量,两者其实可以抽象为统一的“函数的函数”,不过由于两者都涉及到较多的概念,以及实际应用也针对不同的场景,所以在此将其分开。
上图表明两大重要概念“连续”与“极限”在各研究对象之间的关系。其实“数”本身并无极限一说,极限肯定是针对某个过程才有意义的,所以这里指的实际上是整序变量,或者说数列的极限。另外,导函数也是函数,所以对于函数的一切研究方法在导函数里也是适用的,函数的性质与导函数的性质紧密联系。
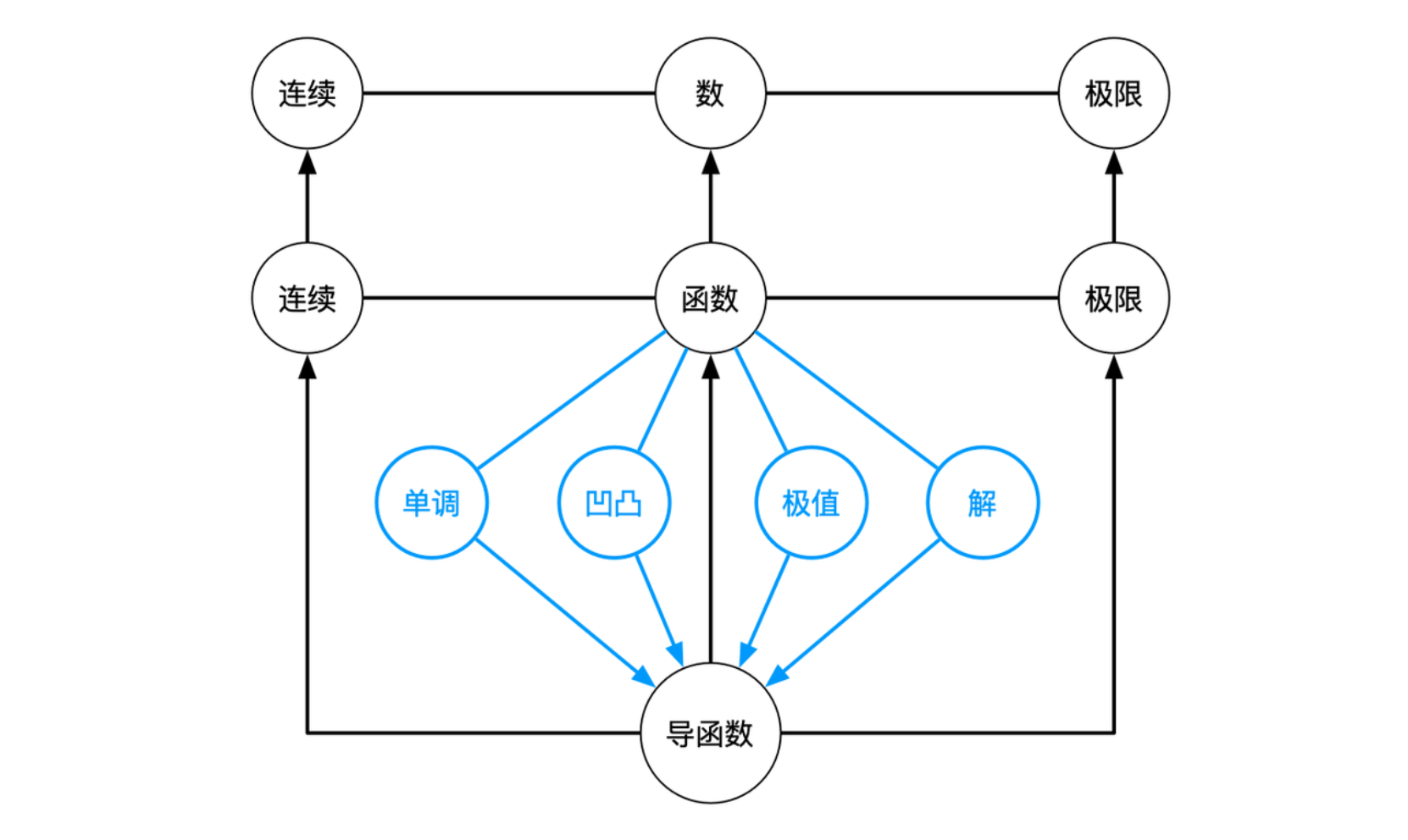
函数里面的子课题,比如函数的单调性,凹凸性,极值,以及求解等问题,都能够通过研究其导函数得出,虽然单调性能够使用比较初等的方法直接通过函数得出(高中数学),但是通过导函数来得到这些结果可以更好地将这两者联系起来,并且这也是更方便更高级的工具。
进一步,上面的函数概念其实并不仅限于“一元函数”,而是广义上的函数,对于一般的教程来说,都会从一元函数开始,然后推广至多元函数,在多元函数的章节,会对一元函数的各种定理进行重新表述。再者,针对导数与微分相关的概念,也会在多元函数进行重述。整理这些知识的最好顺序,我觉得正是课本安排的顺序,但是课本是单向的,而我觉得更重要的一步是在学习多元函数之后对知识进行回顾,然后将多元函数看成是基本情况,而一元函数,只是其简单特例。