极限
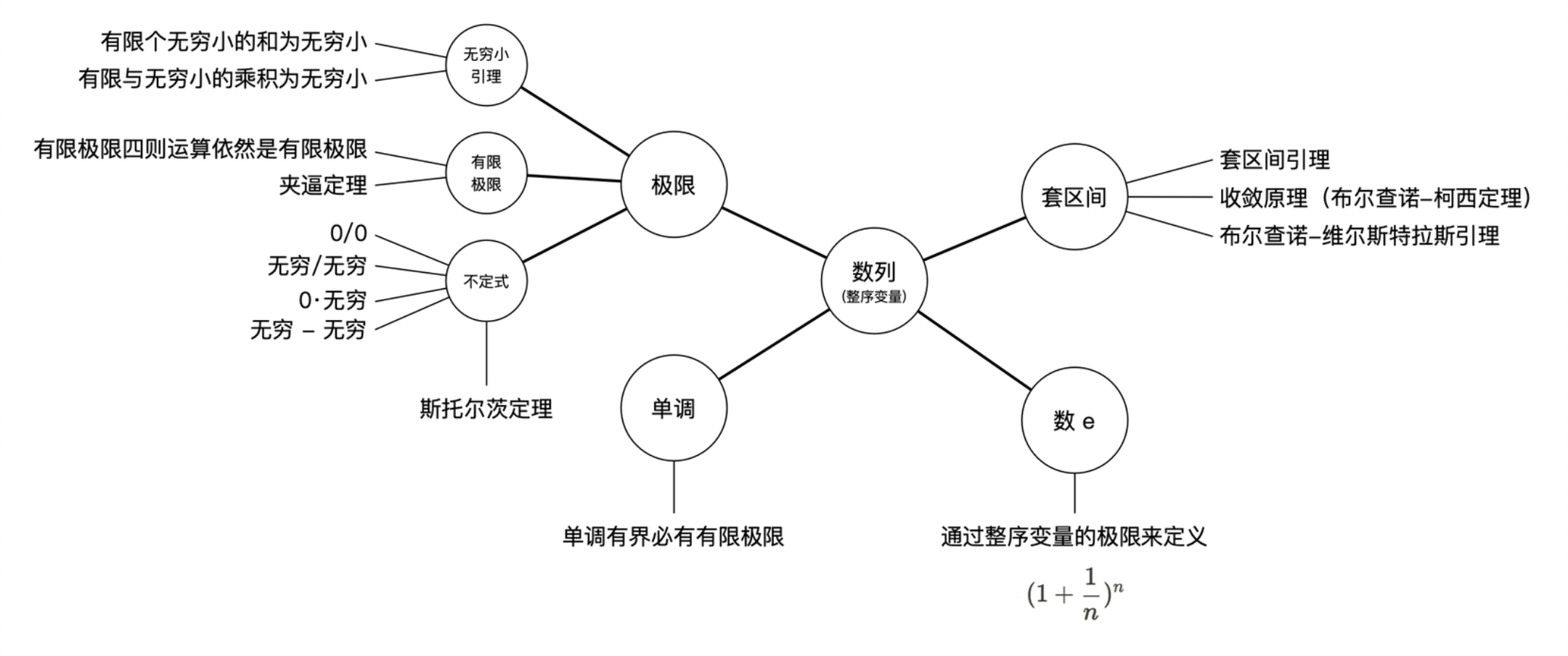
从上面的概念关系图来看,极限实际上是一个通用的概念,其研究变量变化的趋势结果。所以对于一个数来说,不存在“极限”的概念,它必须是针对一系列的数的变化趋势来说的。
整序变量
设有自然数列:
\[ 1, 2, \cdots, n, \cdots, n', \cdots \]
在序列内数字由小而大的顺序排列着,较大的数 \(n'\) 在较小的数 \(n\) 的后面,若在自然数列内,按照任意规律,将每一个自然数 \(n\) 换成实数 \(x_n\),则得到数列
\[ x_1, x_2, x_3, \cdots, x_n, \cdots, x_n', \cdots \]
其项或元素 \(x_n\) 有一切自然数作为序号,并依照序号增大的次序排列,取成该序列的变量 \(x\),称之为整序变量。
整序变量的极限
若对于每一正数 \(\varepsilon\),不论它怎样小,恒有序号 \(N\),使得 \(n > N\) 时,一切 \(x_n\) 的值满足不等式
\[ |x_n - a| < \varepsilon \]
则常数 \(a\) 称为整序变量 \(x = x_n\) 的极限,记为
\[ \lim_{n \to +\infty} x_n = a \]

这意味着,从某一项开始的后面所有项,都在区间 \((a - \varepsilon, a + \varepsilon)\) 里。如果 \(a = 0\),则称 \(x_n\) 为无穷小。如果从某项开始,其绝对值变成且保持着大于预先指定的任意大数 \(E > 0\),\(|x_n| > E\),则称 \(x_n\) 为无穷大。
极限运算
若整序变量 \(x_n\) 与 \(y_n\) 趋于有限极限,则其和差积商均为有限极限。
\[ \lim x_n = a, \lim y_n = b \iff \begin{cases} & \lim(x_n \pm y_n) = a \pm b \\ & \lim x_n y_n = ab \\ & \lim x_n / y_n = a/b \end{cases} \]
若整序变量不趋于有限极限,有几种不定式的情形需要具体情况具体分析,包括
\[ \frac{0}{0}, \ \frac{\infty}{\infty}, \ {0}\cdot{\infty}, \ {\infty} - {\infty} \]
斯托尔茨(O.Stolz)定理
设整序变量 \(y_n \to +\infty\),并且 —— 至少从某一项开始 —— 在 \(n\) 增大时 \(y_n\) 亦增大:\(y_{n+1} > y_n\),则
\[ \lim \frac{x_n}{y_n} = \lim \frac{x_n - x_{n-1}}{y_n - y_{n-1}} \]
数“e”
使用整序变量来对 e 进行定义。令
\[ x_n = (1 + \frac{1}{n})^n \]
则
\[ \lim_{n \to +\infty} x_n = e \]
单调整序变量
这是一种简单,重要, 并且特殊的变量。如果对于整序变量 \(x_n\),有
\[ x_1 < x_2 < \cdots < x_n < x_{n+1} < \cdots \]
就是说,如果 \(n' > n\),则必有 \(x_{n'} > x_n\),这时我们把 \(x_n\) 称为递增的。相应地,可以建立递减的概念。这种向单一方向改变的变量总称为单调变量。
定理:设已给单调增大的整序变量 \(x_n\),若它上有界:
\[ x_n \leq M, M = \text{constant}, n \in \mathbb{Z}^+ \]
则必有一有限的极限,否则极限为 \(+\infty\)。
收敛原理以及部分极限
套区间的引理
设给定单调增大的整序变量 \(x_n\) 及单调减少的整序变量 \(y_n\),且恒有若其差 \(y_n - x_n\) 趋向于 \(0\),则两整序变量必有公共的有限极限:
\[ c = \lim x_n = \lim y_n \]
换一种形式叙述,满足不等式
\[ a \leq x \leq b \]
的一切数(或常说成“点”)\(x\) 所成的集合称为区间 \([a, b]\),数 \(a\) 及 \(b\) 各称为区间的左端点与区间的右端点,其差 \(b - a\) 称为区间的长。若区间 \([a', b']\) 的的一切点多属于区间 \([a, b]\),即
\[ a \leq a' < b' \leq b \]
则约定说,区间 \([a', b']\) 包含在区间 \([a, b]\) 内,或者说“被套在里面”。设有一区间套的无穷序列
\[ [a_1, b_1], [a_2, b_2], \cdots, [a_n, b_n], \cdots \]
后一个总是套在前一个内,并且在 \(n\) 增大的时候这些区间的长度趋于 \(0\)
\[ \lim (b_n - a_n) = 0 \]
则区间的端点 \(a_n\) 与 \(b_n\) 趋于公共的极限
\[ c = \lim a_n = \lim b_n \]
收敛原理(柯西 - 布尔查诺定理)
整序变量 \(x_n\) 有有限极限的必要且充分条件是:对于每一个数 \(\varepsilon > 0\) 总存在着序号 \(N\),使得当 \(n > N\) 及 \(n > N'\) 时,便能成立不等式
\[ |x_n - x_{n'}| < \varepsilon \]
布尔查诺 - 维尔斯特拉斯引理
由任何有界数列内恒能选出收敛于有限极限的部分数列。