函数
设给定两变量 \(x\) 及 \(y\),其变动区域为 \(\mathcal{X}\) 及 \(\mathcal{Y}\),假定根据问题的条件,变量 \(x\) 可以不受任何限制地取区域 \(\mathcal{X}\) 内的任意数值,那么,如果依某一法则或者规律,对于 \(\mathcal{X}\) 中的每一 \(x\) 值总有一个确定的数值 \(y\)(在 \(\mathcal{Y}\) 内)和它对应,则变量 \(y\) 就称为变量 \(x\)(在它的变动区域 \(\mathcal{X}\) 内)的函数。记作
\[ y = f(x), x \in \mathcal{X}, y \in \mathcal{Y} \]
其中 \(x\) 称为自变量,\(y\) 称为因变量,\(\mathcal{X}\) 称为定义域,\(\mathcal{Y}\) 称为值域。(当然,还会有很多其他表示方式,比如 \(f: \mathcal{X} \to \mathcal{Y}\),\(y = y(x)\) 等等)
初等函数
有理整函数及分式函数
表示为 \(x\) 的多项式的函数
\[ y = a_0 x^n + a_1 x^{n-1} + \cdots + a_n = \sum_{i = 0}^n a_i x^{n-i}, \ (a_i \in \mathbb{R}) \]
称为有理整函数,而两个这样的多项式之比
\[ y = \frac{a_0 x^n + a_1 x^{n-1} + \cdots + a_n}{b_0 x^m + b_1 x^{m-1} + \cdots + b_m} = \frac{\sum_{i = 0}^n a_i x^{n-i}}{\sum_{j = 0}^m b_j x^{m-j}}, (a_i, b_i \in \mathbb{R}) \]
称为有理分式函数。
幂函数
形如
\[ y = x^\mu, (\mu \in \mathbb{R}) \]
的函数称为幂函数。当 \(\mu\) 为整数时便为有理整函数。\(\mu\) 为分数时变得根数,比如
\[ y = x^{\frac{1}{m}} = \sqrt[m]x, m \in \mathbb{N} \]
对于幂函数来说,定义域取决于 \(\mu\),如果 \(\mu\) 为偶数,则定义域只能是非负数。
指数函数
形如
\[ y = a^x, x \in \mathbb{R} \]
的函数为指数函数。
对数函数
形如
\[ y = \log_a x, a > 0, x > 0 \]
的函数为指数函数。
三角函数
\[ \begin{aligned} y &= \sin x, \ x \in \mathbb{R} \\ y &= \cos x, \ x \in \mathbb{R} \\ y &= \tan x, \ x \neq k\pi + \pi/2, k \in \mathbb{Z} \\ y &= \sec x, \ x \neq k\pi + \pi/2, k \in \mathbb{Z} \\ y &= \cot x, \ x \neq k\pi, k \in \mathbb{Z} \\ y &= \csc x, \ x \neq k\pi, k \in \mathbb{Z} \end{aligned} \]
双曲函数
双曲函数定义如下
\[ \begin{aligned} \sinh x &= \frac{e^x - e^{-x}}{2}, \\ \cosh x &= \frac{e^x + e^{-x}}{2}, \\ \tanh x &= \frac{\sinh x}{\cosh x} = \frac{e^x - e^{-x}}{e^x + e^{-x}}, \\ \coth x &= \frac{\cosh x}{\sinh x} = \frac{e^x + e^{-x}}{e^x - e^{-x}}, \end{aligned} \]
从上到下分别为双曲正弦,双曲余弦,双曲正切以及双曲余切。它们对于 \(x \in \mathbb{R}\) 有意义,除了 \(\coth x\) 在 \(x = 0\) 的时候没定义。
反三角函数
\[ \begin{aligned} y &= \arcsin x \\ y &= \arccos x \\ y &= \arctan x \\ y &= \text{arccot} x \end{aligned} \]
对于 \(y = \arcsin x\) 来说,\(x \in [-1, 1]\) 内有定义,并且是多值的,因为 \(y\) 延纵轴方向周期性波动,所以称 \(y \in [-\frac{\pi}{2}, \frac{\pi}{2}]\) 为主值。
反函数
假定在某一区域 \(\mathcal{X}\) 内给定函数 \(y = f(x)\),并设当 \(x\) 在区域 \(\mathcal{X}\) 内变动的时候,一切函数值所成的集合为 \(\mathcal{Y}\)(即为满射)。在区域 \(\mathcal{Y}\) 内选取任一数值 \(y = y_0\),则在区域 \(\mathcal{X}\) 内必能求出数值 \(x = x_0\),使得函数在 \(x_0\) 所取的数值就是 \(y_0\),即
\[ f(x_0) = y_0 \]
像这样的数值 \(x_0\) 可能出现很多个,因此,\(\mathcal{Y}\) 内的任一数值 \(y\) 将与一个或几个 \(x\) 的数值相对应,由此对应地确定在区域 \(\mathcal{Y}\) 内的单值或多值函数 \(x = g(y)\),它就称为函数 \(y = f(x)\) 的反函数。
存在条件
设函数 \(y = f(x)\) 是在某一区间 \(\mathcal{X}\) 内定义的,它连续而且单调增大(或减小),则在对应的函数值所成的区间 \(\mathcal{Y}\) 内必存在单值的反函数 \(x = g(y)\),也是连续而且单调增大(或减小)。
函数的极限
考察数集 \(\mathcal{X} = \{x\}\),以点 \(a\) 为中心点的开区间 \((a - \delta, a + \delta)\) 称为点 \(a\) 的邻域。如果在点 \(a\) 的任一邻域内包含 \(\mathcal{X}\) 中异于 \(a\) 的 \(x\) 值,则点 \(a\) 为数集 \(\mathcal{X}\) 的聚点。点 \(a\) 不一定需要在 \(\mathcal{X}\) 里。
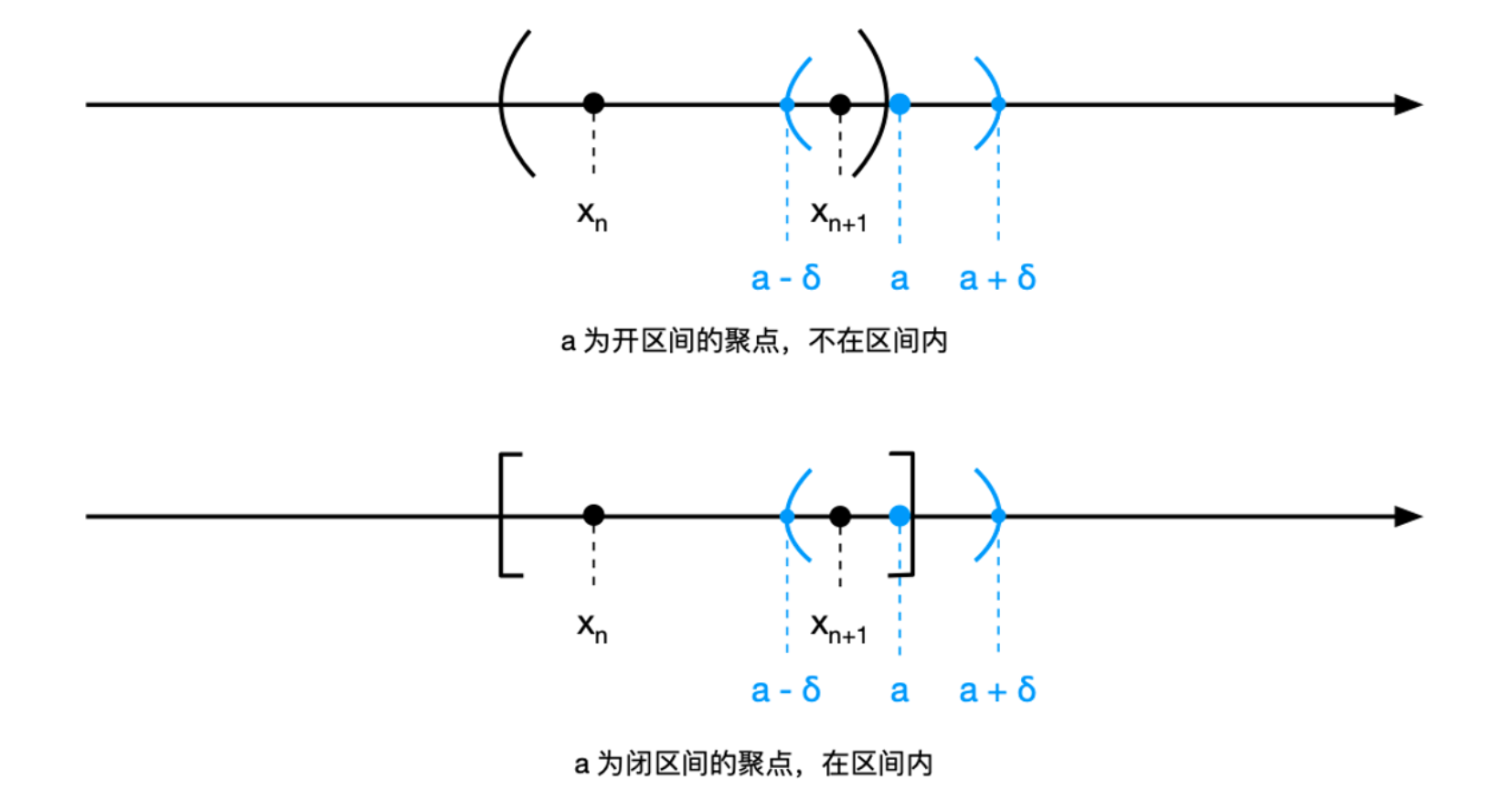
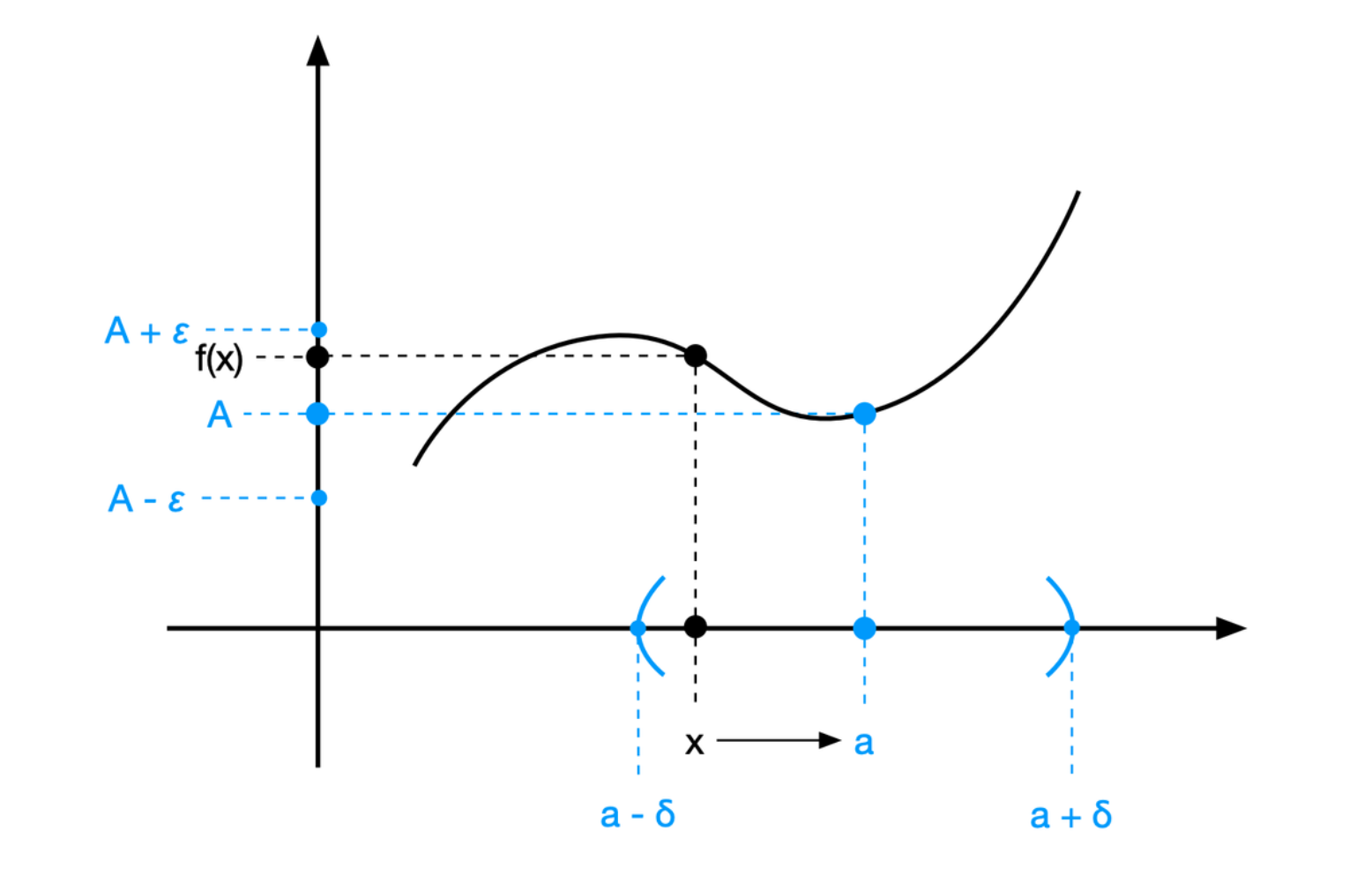
设在区域 \(\mathcal{X}\) 内给定函数 \(f(x)\),且 \(a\) 是 \(\mathcal{X}\) 的聚点。这函数在 \(x\) 接近于 \(a\) 的性态是值得注意的。若对于任一数 \(\varepsilon > 0\),能求出数 \(\delta > 0\),只需 \(|x - a| < \delta\), 能使
\[ |f(x) - A| < \varepsilon \]
则称当 \(x\) 趋于 \(a\) 时(或在 \(a\) 点处)函数 \(f(x)\) 以数 \(A\) 为极限。记为
\[ \lim_{x \to a} f(x) = A \]
左右极限
设 \(\mathcal{X}\) 是这样的一种区域,仅在 \(a\) 的右边任意近处,能找出 \(\mathcal{X}\) 内的异于 \(a\) 的 \(x\) 数值(这种情况下点 \(a\) 称为 \(\mathcal{X}\) 的右聚点),则可以把函数极限的定义特殊化,使仅限于 \(x > a\) 的数值。在这种场合,如果函数的极限存在,就称为当 \(x\) 从右边趋向于 \(a\) 时函数 \(f(x)\) 的极限,或简称右极限,并记作
\[ \lim_{x \to a+0} f(x) \]
同理可以定义左极限,记为
\[ \lim_{x \to a-0} f(x) \]
一些重要的极限
三角函数相关
\[ \lim_{x \to 0} \frac{\sin x}{x} = 1 \]
数 \(e\) 相关
\[ \lim_{x \to \infty} (1 + \frac{1}{x})^x = e \]
令 \(x = 1/a\),有
\[ \lim_{a \to 0} (1 + a)^{\frac{1}{a}} = e \]
存在条件(布尔查诺 - 柯西的一般判定法)
函数 \(f(x)\) 当 \(x\) 趋于 \(a\) 时有一有限极限的必要且充分条件是,对于任一数 \(\varepsilon > 0\) 必存在 \(\delta > 0\)。只需 \(|x - a| < \delta,\ |x' - a| < \delta\),就能成立不等式 \(|f(x) - f(x')| < \varepsilon\)。
无穷小及无穷大的阶
有两无穷小量 \(\alpha\) 和 \(\beta\)
- 若比式 \(\beta / \alpha\) 有一异于零的有限极限,则无穷小 \(\alpha\) 与 \(\beta\) 称为同阶的。
- 若比式 \(\beta / \alpha \to 0\),则无穷小 \(\beta\) 称为是比 \(\alpha\) 高阶的无穷小,而无穷小 \(\alpha\) 为比 \(\beta\) 低阶的无穷小。若无穷小 \(\beta\) 比无穷小 \(\alpha\) 更高阶,则记为 \(\beta = o(\alpha)\)。
- 若 \(\beta\) 与 \(\alpha^k(k > 0)\) 是同阶无穷小,即若比式 \(\beta / \alpha^k\) 有异于零的有限极限,则称无穷小 \(\beta\) 为关于基本无穷小 \(\alpha\) 的 \(k\) 阶无穷小量。
- 无穷小 \(\alpha\) 与 \(\beta\) 称为等价无穷小(记为 \(\alpha \sim \beta\)),若它们的差 \(\gamma = \beta - \alpha\) 是比 \(\alpha\) 及 \(\beta\) 中的任何一个更高阶的无穷小,即 \(\gamma = o(\alpha)\) 及 \(\gamma = o(\beta)\)。
使两个无穷小 \(\alpha\) 与 \(\beta\) 成为等价的,充要条件是
\[ \lim \frac{\beta}{\alpha} = 1 \]
主部的分出 若选定 \(\alpha\) 为基本无穷小,则形如 \(c \cdot \alpha^k\) 的量自然就认为是最简单的无穷小,此处的 \(c\) 是非零常系数,而 \(k > 0\),设 \(\beta\) 是关于 \(\alpha\) 的 \(k\) 阶无穷小,即
\[ \lim \frac{\beta}{\alpha^k} = c \]
则
\[ \lim \frac{\beta}{c\alpha^k} = 1 \]
即 \(\beta \sim c\alpha^k\),这个 \(c\alpha^k\) 就称为 \(\beta\) 的主部。
将上述论断稍作修改便可得到有关无穷大的阶的相关描述。
函数的连续与间断
连续与间断
定义在以 \(x_0\) 为聚点的某个区域 \(\mathcal{X} = \{x\}\) 内的函数 \(f(x)\),并设 \(x_0 \in \mathcal{X}\),于是在这点函数有确定的数值 \(f(x_0)\),如果有
\[ \lim_{x \to x_0} f(x) = f(x_0) \]
则说函数 \(f(x)\) 当 \(x = x_0\) 时(或在点 \(x = x_0\) 处)是连续的,如果上式不成立,则说函数 \(f(x)\) 在 \(x = x_0\) 处间断。(\(x\) 甚至不需要在定义域里)
也可以使用“\(\varepsilon - \delta\) 语言”定义:函数 \(f(x)\) 在点 \(x_0\) 处的连续性的意义可以归结为,对于任意的 \(\varepsilon > 0\),必能求出 \(\delta > 0\),使得由
\[ |x - x_0| < \delta \implies |f(x) - f(x_0)| < \varepsilon \]
如果函数在 \(\mathcal{X}\) 内的每一点都是连续的,就说函数在区间 \(\mathcal{X}\) 内是连续的。
- 所有初等函数都是连续的。
- 连续函数的算术运算也都是连续的。
- 连续函数的组合也是连续的。
单侧连续与单侧极限类似,只需要稍微修改上述定义即可。
\[ \begin{aligned} \lim_{x \to x_0 + 0} f(x) &= f(x_0) \\ \lim_{x \to x_0 - 0} f(x) &= f(x_0) \\ \end{aligned} \]
间断点的分类
如果在某点 \(x = x_0\) 单侧极限存在,即 \(\lim_{x \to x_0} f(x)\) 存在,但是不等于 \(f(x_0)\),这种间断称为普通间断或第一类间断。如果极限 \(\lim_{x \to x_0} f(x)\) 不存在,则称为第二类间断。
狄利克雷函数
\[ \chi(x) = 1,\ x 是有理数 \\ \chi(x) = 0,\ x 是无理数 \]
因为在有理点的任意近处总有无理点,反过来也是如此,所以不论 \(x_0\) 是区间 \((-\infty, +\infty)\) 内怎样的点,当 \(x \to x_0\) 时 \(\chi(x)\) 没有极限存在,因为函数再任一点处有第二类的两方间断。
单调函数的连续性及间断
单调增(减)函数 \(f(x)\) 在 \(\mathcal{X}\) 内若有间断,只能有第一种间断,即跃度。
若在区间 \(\mathcal{X}\) 内为单调增大(减少)的函数 \(f(x)\) 的数值都包含在区间 \(\mathcal{Y}\) 内,且把它全部填满(即满射),则这函数在 \(\mathcal{X}\) 内是连续的。
连续函数的性质
零值定理
布尔查诺 - 柯西第一定理 设函数 \(f(x)\) 是在闭区间 \([a, b]\) 内定义着并且连续的,又在这区间的两端点处取得异号的数值,则在 \(a\) 与 \(b\) 之间必能求出一点 \(c\),在这点处函数为零。
介值定理
布尔查诺 - 柯西第二定理 设函数 \(f(x)\) 是在某一区间 \(\mathcal{X}\)(闭的或不闭的,有限的甚至无穷的都可以)内定义着并且连续的,若在这区间内的两点 \(x = a\) 及 \(x = b \ (a < b)\) 处函数具有不相等的数值 \(f(a) = A\) 以及 \(f(b) = B\),则对于 \(A\) 与 \(B\) 之间的任意数 \(C\) 必能求出 \(a\) 与 \(b\) 之间的点 \(x = c\),使得 \(f(c) = C\)。
闭区间有界性
魏尔斯特拉斯第一定理 若函数 \(f(x)\) 是在闭区间 \([a, b]\) 内定义并且是连续的,则它必是有界的,即必存在着有限的常数 \(m\) 以及 \(M\),使当 \(a \leq x \leq b\) 时,有 \(m \leq f(x) \leq M\)。
魏尔斯特拉斯第二定理 若函数 \(f(x)\) 是在闭区间 \([a, b]\) 内定义并且是连续的,则它在这区间内必能达到自己的上确界以及下确界。
一致连续
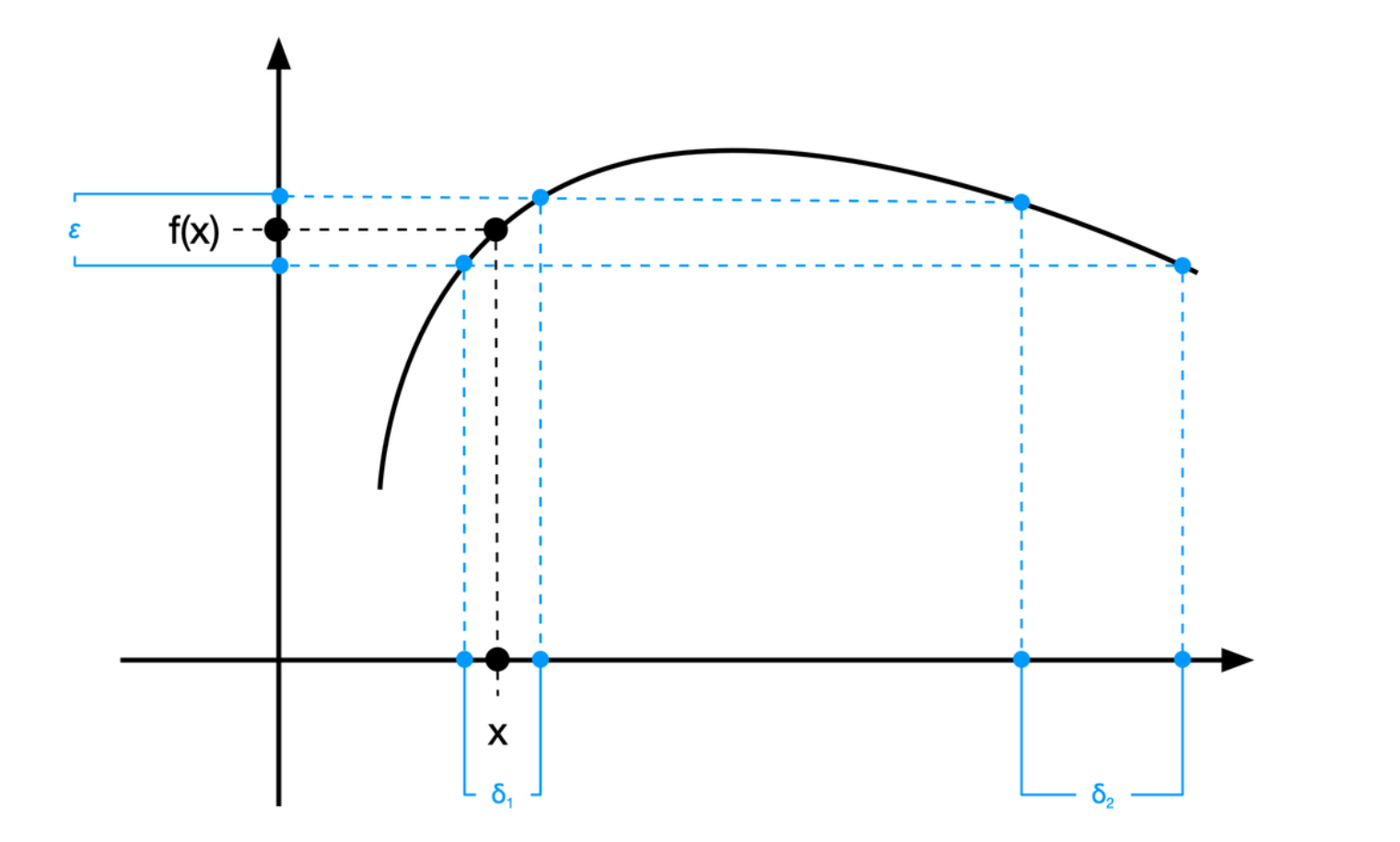
若对于任一数 \(\varepsilon > 0\) 能求出数 \(\delta > 0\),使由 \(|x - x_n| < \delta\) 就能推出 \(|f(x) - f(x_0)| < \varepsilon\),不论点 \(x_0\) 及 \(x\) 是在区间 \(\mathcal{X}\) 内的什么地位,则函数 \(f(x)\) 称为在区间 \(\mathcal{X}\) 内是一致连续的。
康托定理
若函数 \(f(x)\) 是在闭区间 \([a, b]\) 内定义着而且连续,则它在这区间也是一致连续的。
推论 设函数 \(f(x)\) 是在闭区间 \([a, b]\) 内定义着而且连续的。则依给定的 \(\varepsilon > 0\) 能求出这样的 \(\delta > 0\),若把区间任意分成长度小于 \(\delta\) 的部分区间,则在每一个部分区间内函数 \(f(x)\) 的振幅将小于 \(\varepsilon\)。
博雷尔引理
若闭区间 \([a, b]\) 被一个开区间的无穷系 \(\Sigma = \{ \sigma \}\) 所覆盖,则恒能从 \(\Sigma\) 里面选出有限子系
\[ \Sigma^* = \{ \sigma_1, \sigma_2, \dots, \sigma_n\} \]
它同样能覆盖全区间 \([a, b]\)。
需要注意的是,基本区间 \([a, b]\) 是闭区间以及 \(\Sigma\) 中的区间 \(\sigma\) 是开区间这两个假定对于引理的结论的真实性是同等重要的。例如,开区间
\[ (\frac{1}{2}, \frac{3}{2}), (\frac{1}{4}, \frac{3}{4}), (\frac{1}{8}, \frac{3}{8}), \cdots, (\frac{1}{2^n}, \frac{3}{2^n}), \cdots \]
的全体覆盖区间 \((0, 1]\),但从中却不能选出具有同样性质的有限子系。又如,闭区间
\[ [0, \frac{1}{2}], [\frac{1}{2}, \frac{3}{4}], [\frac{3}{4}, \frac{7}{8}], \cdots, [\frac{2^n - 1}{2^n}, \frac{2^{n+1} - 1}{2^{n+1}}], \cdots, [1, 2] \]
能覆盖 \([0, 2]\),但也不能从中选出具有同样性质的有限子系。