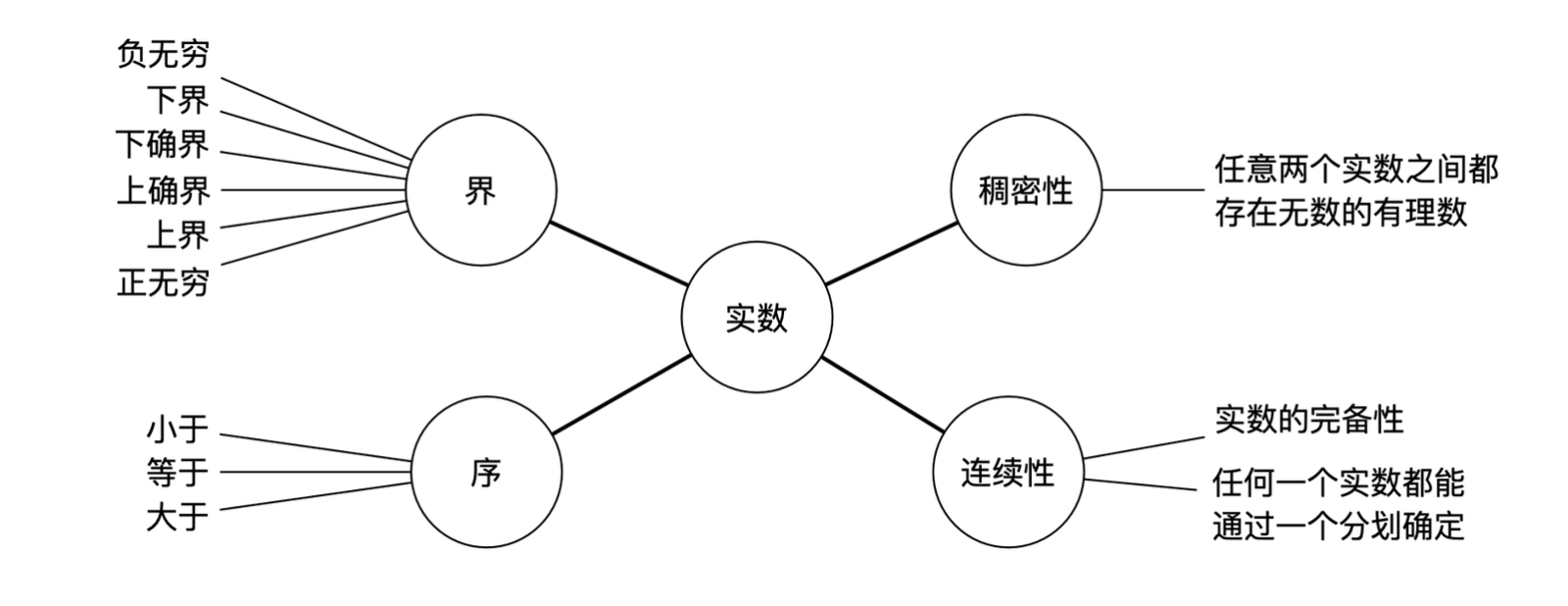
实数
在历史的长河里,数集不断被扩充,从正整数开始,扩充到整数,到有理数,再到无理数,在实分析的范畴内,数集为我们所熟知的实数 \(\mathbb{R}\)。
定义
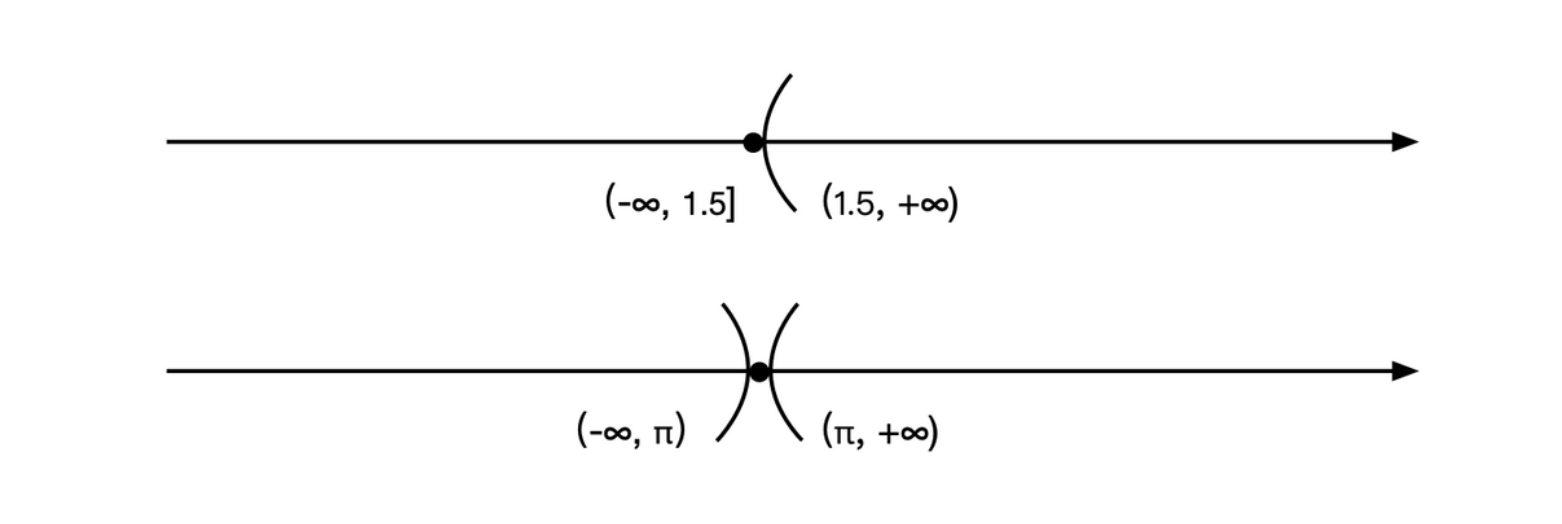
通过对有理数分划进行定义而引入无理数的概念。满足下面条件的称为一个分划:
- 任一有理数,必在且仅在 \(A\) 及 \(A'\) 二集之一中出现;
- 集 \(A\) 内的任一数 \(a\),必小于集 \(A'\) 内的任一数 \(a'\)。
分划记为 \(A | A'\)。
分划有三种类型
- 在下组 \(A\) 内无最大数,而在上组 \(A'\) 内有最小数 \(r\);
- 在下组 \(A\) 内有最大数 \(r\),而在上组 \(A'\) 内无最小数;
- 在下组 \(A\) 内无最大数,而在上组 \(A'\) 内亦无最小数。
对于前两种情况,我们说,分划由有理数 \(r\) 所产生,或者说分划定义有理数 \(r\)。对于第三种情况,我们约定分划定义一个无理数 \(\alpha\),这个数代替了缺少的界数。
序
由分划 \(A|A'\) 及 \(B|B'\) 所确定的两个无理数 \(\alpha\) 和 \(\beta\),当且仅当两个分划恒等时,始认为相等,即 \(\alpha = \beta\)。而有较大下组的那个分划,确定的数更大,即如果 \(A \subset B\),则 \(\alpha < \beta\)。
稠密性
对于任意两个实数 \(\alpha\) 与 \(\beta\),其中 \(\alpha > \beta\),恒存在一个位于其中的有理数,即 \(\alpha > r > \beta\)(因此,这种有理数是有无数个的)。
设给定两个实数 \(\alpha\) 和 \(\beta\),如果任取一个 \(e > 0\),数 \(\alpha\) 与 \(\beta\) 都能位于同一对有理数 \(s\) 与 \(s'\) 之间:
\[ s'>\alpha>s \\ s'>\beta>s \]
这对数的差小于 \(e\):
\[ s' - s < e \]
则数 \(\alpha\) 与 \(\beta\) 必须相等。
连续性
引入无理数的目的,是为了填补有理数的空隙。有以下基本定理。
实数域上的这个性质通常称为它的完备性,也称为它的连续性。
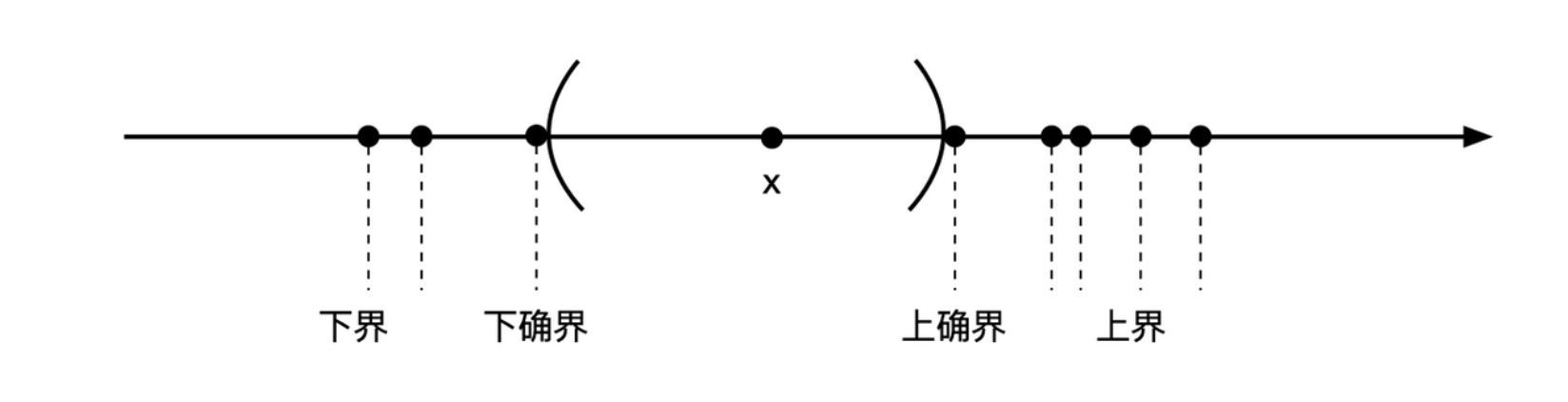
数集的界
设实数的任一无限集,集合内的任一数为 \(x\),记集合为 \(\chi = \{x\}\),对所考察的集合 \(\{x\}\),存在 \(M\) 使得一切的 \(x \leq M\),则说该集合上有界,而 \(M\) 就是该集合的上界。而上界有无穷多个,其中最小的为上确界。相应地有下有界,下界以及下确界的概念。
如果数集不上(下)有界,则称 \(+\infty\)(\(-\infty\))为其上(下)界。